Sternengeschichten Folge 617: Metriken der Raumzeit

Das ist die Transkription einer Folge meines Sternengeschichten-Podcasts. Die Folge gibt es auch als MP3-Download und YouTube-Video. Und den ganzen Podcast findet ihr auch bei Spotify.

Mehr Informationen: [Podcast-Feed][Apple]Spotify][Facebook][Twitter]

Wer den Podcast finanziell unterstützen möchte, kann das hier tun: Mit PayPal, Patreon oder Steady.

Über Bewertungen und Kommentare freue ich mich auf allen Kanälen.

Sternengeschichten Folge 617: Metriken der Raumzeit

In dieser Folge der Sternengeschichten wird es ein wenig mathematisch. Ich werde vielleicht Begriffe verwenden wie „Differentialgeometrie“, „Metrischer Tensor“ oder „Minkowski-Raum“. Oder nicht, mal schauen. Aber keine Sorge: Ich werde mein Bestes geben, damit am Ende alle verstehen worum es geht und es lohnt sich, zu verstehen, worum es geht, denn es geht um nichts weniger als die Form des Universums.

Aber dafür müssen wir trotzdem mit der Metrik anfangen. Dieses Wort kann verschiedene Bedeutungen haben; in der Literatur beschreibt es das Versmaß von Gedichten, in der Musik die Art und Weise wie Noten betont werden und das ist zwar alles sehr spannend – wir bleiben aber trotzdem bei der mathematischen Bedeutung. Und da ist eine Metrik eine Funktion, die zwei Punkten im Raum eine Zahl zuordnet, die man als Abstand dieser beiden Punkte definieren kann.

Warum so kompliziert, mag sich jetzt der eine oder die andere denken. Wenn ich den Abstand zwischen zwei Punkten messen will, dann mess ich den halt einfach! Warum braucht es da eine Funktion, die eine Zahl „zuordnet“, die als Abstand „definiert“ werden kann? Weil es halt erstens nicht so einfach ist und wir zweitens genau sein wollen, immerhin geht es um das Universum.

Ja, ich kann ein Blatt Papier nehmen, zwei Punkte draufmalen und dann mit einem Lineal den Abstand messen. Aber wenn ich das tue, dann wende ich – aus mathematischer Sicht – die sogenannte „euklidische Metrik“ an, benannt nach dem griechischen Gelehrten Euklid, der vor langer Zeit die Grundlagen der Geometrie erforscht hat. Wenn wir mit dem Lineal den Abstand zwischen den Punkten messen, dann messen wir ja eigentlich die Länge einer Linie, die die beiden Punkte verbindet. Ich kann jetzt aber sehr einfach mit dieser Linie ein rechtwinkeliges Dreieck konstruieren. Das erklärt sich in einem Podcast viel schwieriger als es in der Praxis ist. Aber wenn ich ausgehend von dem einem Punkt eine Linie ziehe, die parallel zur einen Seite des Blattes verläuft und ausgehend vom anderen Punkt eine Parallele zur anderen Blattseite, dann schneiden die sich in einem rechten Winkel. Und mit der Verbindungslinie zwischen den beiden Punkten kriege ich ein rechtwinkeliges Dreieck. Und was gilt bei einem rechtwinkeligen Dreieck? Genau, der Satz von Pythagoras, den wir alle aus der Schule kennen. a²+b²=c². Oder anders gesagt: Ich kann die Länge der Verbindungslinie berechnen, wenn ich die Länge der beiden anderen Seiten kenne und die kenne ich, weil ich ja weiß, wo die Punkte sind. Oder nochmal anders und mathematisch genauer gesagt: Aus den zweidimensionalen Koordinaten meiner beiden Punkte kann ich – mit dem Satz von Pythagoras – sehr leicht eine Funktion definieren, die mir als Ergebnis den direkten Abstand der Punkte liefert. Wer es genau wissen will: Wenn die Koordinaten der beiden Punkte x1/y1 und x2/y2 sind, dann beträgt der Abstand zwischen ihnen genau (x2-x1)² + (y2-y1)² und daraus noch die Wurzel.

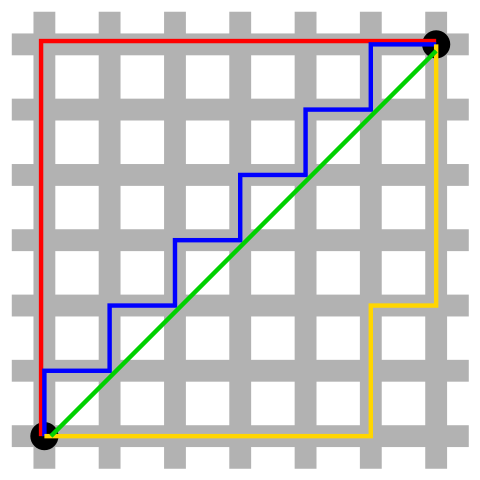
Ich weiß, das waren jetzt schon viele Zahlen und Formeln. Aber wenn man ein bisschen drüber nachdenkt, war es auch nicht schlimm. Und notwendig, weil wir dieses Konzept der Metrik wirklich brauchen, wenn wir die Form des Universums verstehen wollen. Beziehungsweise nicht dieses spezielle Konzept der euklidischen Metrik, aber die allgemeine Idee. Denn es gibt jede Menge Metriken! Das mag überraschend klingen – wieso braucht man mehr als eine Art, einen Abstand zu definieren? Entweder zwei Punkte sind 10 Meter voneinander entfernt oder nicht? Aber wie gesagt: So einfach ist es nicht. Stellt euch mal vor, ihr seid in New York, in Manhattan, wo die Straßen ein Gitter bilden. Wenn ich jetzt wissen will, wie weit es von einer Ecke in Manhattan zu einer anderen ist, dann hilft mir die euklidische Metrik wenig. Die gibt mir ja den direkten Abstand, also quasi die Luftlinie. Und wenn ich nicht mit dem Flugzeug unterwegs bin, dann hilft mir das nichts. Ich kann ja nicht schnurgerade durch die Stadt gehen, Hochhäuser raufklettern und wieder runter. Ich muss den Straßen und den rechten Winkeln folgen. Und brauche deswegen eine andere Funktion, mit der ich den Abstand berechnen kann beziehungsweise eine andere Metrik. Die heißt übrigens auch „Manhattan-Metrik“ und hat tatsächlich Anwendungen abseits der Navigation durch amerikanische Großstädte, aber das würde jetzt zu weit führen.

Wir wollen uns ja um das Universum kümmern. Und auch da kommen wir mit der euklidischen Metrik nicht weit. Zuerst mal, weil das Universum kein zweidimensionales Blatt Papier ist. Wir haben drei Raumdimensionen, was aber noch kein Problem wäre. Das mit den Dreiecken und der euklidischen Metrik lässt sich problemlos auf drei Dimensionen erweitern. Aber der Raum ist ja nicht nur dreidimensional, sondern auch gekrümmt. Das wissen wir dank Albert Einsteins Allgemeiner Relativitätstheorie und das macht die Sache schwierig. Jede Masse krümmt den Raum und wir müssen trotzdem einen Weg finden, um die Abstände zu bestimmen.

Stellen wir uns nochmal das Blatt Papier vor. Nur legen wir es jetzt nicht flach auf den Boden, sondern streuen vorher noch nen Haufen unterschiedlich große Murmeln aus und legen das Blatt darauf. Jetzt wird es jede Menge Buckel im Papier geben und wir kommen mit den Dreiecken und dem Satz von Pythagoras nicht mehr weiter, wenn wir den kürzesten Abstand zwischen zwei Punkten messen wollen. Die Linien, die wir zwischen den Punkten ziehen, werden gebogen sein; wir können sie um die Buckel herum ziehen oder oben drüber – aber es ist nicht auf den ersten Blick ersichtlich, welche davon länger oder kürzer sind.

Dasselbe Problem haben wir auch beim Universum. Der Raum ist gekrümmt und im Prinzip an jedem Punkt unterschiedlich stark. In der Nähe von Sternen stärker als im leeren Weltraum; in der Umgebung von schwarzen Löchern so stark, dass wir uns schwer tun zu verstehen, was da abgeht. Und so weiter. Aber trotzdem wollen wir das irgendwie untersuchen können, zumindest mathematisch. Genau das war das Problem, vor dem Albert Einstein gestanden ist, als er seine Allgemeine Relativitätstheorie formuliert hat. Zu sagen: „Massen krümmen die Raumzeit“ und „Objekte folgen bei ihrer Bewegung der Krümmung“ ist das eine. Das auch mathematisch exakt aufzuschreiben, das andere. Aber am Ende hat Einstein es geschafft und das Ergebnis waren seine berühmten Feldgleichungen. Ich erspare es mir (und euch), die jetzt im Detail zu erklären. Aber im Wesentlichen ist ein Satz von mathematischen Gleichungen, bei denen auf der einen Seite ein Krümmungstensor steht und auf der anderen der Energie-Impuls-Tensor.

Und vor dem Wort „Tensor“ muss man auch keine Angst haben, das ist eigentlich nur ein aufgemotzter Vektor. Und was ein Vektor ist, ist simpel. Ein Vektor ist eine Zahl mit einer Richtung. Ok, das ist vielleicht ein bisschen zu vereinfacht. Aber nehmen wir zum Beispiel die Geschwindigkeit. Wenn ich sage, dass ich mit 25km/h die Straße entlang fahre, dann meine ich normalerweise auch genau das: Gemessen an der Distanz die ich auf der Straße zurücklege, bewege ich mich mit 25km/h. Ich kann aber genau so gut sagen, dass ich mich gerade mit 17,7 km/h Richtung Norden und gleichzeitig mit 17,7 km/h in Richtung Westen bewege, nämlich dann, wenn die Straße exakt in Richtung Nordwesten verläuft. Auf der Straße interessiert mich das normalerweise nicht, aber ganz allgemein ist es durchaus sinnvoll, bei einer Geschwindigkeit nicht den absoluten Wert anzugeben, sondern den Anteil, mit dem man sich jeweils in eine der drei Raumrichtungen bewegt. Statt einer Zahl hat man also jetzt drei Zahlen, die man braucht, um zu sagen, wie schnell etwas ist und diese drei Zahlen zusammen sind ein Vektor.

Man kann das Konzept von Vektoren auch ohne physikalische Anwendung und ganz abstrakt definieren; man kann mit Vektoren rechnen wie mit normalen Zahlen; zumindest dann, wenn man die entsprechenden Rechenregeln kennt. Und so weiter. Und man kann das Konzept des Vektors noch erweitern. Einen Vektor kann man sich als eine Liste von Zahlen vorstellen, im Beispiel der Geschwindigkeit eben als Liste von drei Zahlen. Einen Tensor kriege ich, wenn ich aus der Liste eine Tabelle mache. Klingt kompliziert, aber stellen wir es uns so vor: Angenommen wir haben irgendein Material, das sich verformen lässt. Ich kann in der einen Richtung dran ziehen, in der anderen Richtung, ich kann es zusammendrücken, verdrehen, und so weiter. Es ist klar, dass auch hier die Richtung eine Rolle spielt. Vielleicht ist das Material sehr leicht zu dehnen, wenn ich in die eine Richtung ziehen, aber sehr schwer, wenn man an den anderen Seiten zieht? Will man das mathematisch beschreiben, dann muss man das Verhalten für jede Richtung definieren. Und um dieses Verhalten zu beschreiben, brauche ich im Allgemeinen ebenfalls mehr als nur eine Zahl, weil es zum Beispiel davon abhängt, wie schnell die Verformung abläuft und die Geschwindigkeit, wie wir ja schon wissen, ein Vektor mit drei Zahlen ist.

Um das Verzerrverhalten zu beschreiben kriege ich am Ende also einen Vektor, bei der jeder Eintrag selbst wieder ein Vektor ist. Oder, wenn ich das ganze ein wenig anders aufschreibe, eine Tabelle aus Zahlen, die in der Mathematik eine „Matrix“ genannt wird. Oder, noch genauer, als „Tensor zweiter Stufe“. Ein Vektor ist dann ein Tensor erster Stufe, weil die Zahlen hier – vereinfacht gesagt – nur eine Spalte bilden, während sie bei einer Matrix in Spalten und Reihen, also zweidimensional, organisiert sind. Eine simple Zahl, ohne irgendwas, wäre dann logischerweise ein Tensor nullter Stufe und nach oben kann man das auch beliebig erweitern. Ich kann meine Zahlen auch in einem dreidimensionalen Gitter anordnen, wenn das nötig ist und kriege einen Tensor dritter Stufe, und so weiter. Irgendwann kann man sich das nicht mehr vorstellen, aber mathematisch aufschreiben und damit rechnen ist kein Problem.

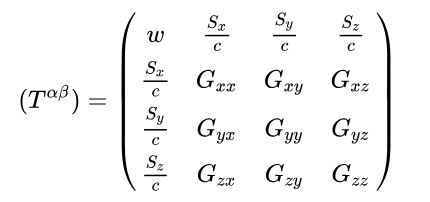
Aber jetzt wieder zurück zu Einstein und seinen Gleichungen. Mit simplen Zahlen kommt man da nicht weit, mit Vektoren auch nicht. Wir haben ja nicht nur einen dreidimensionalen Raum sondern genaugenommen eine vierdimensionale Raumzeit. Und wenn ich beschreiben will, wie die gekrümmt werden kann, dann muss man das so ähnlich anstellen, wie ich es gerade im Beispiel des verzerrten Materials erklärt habe. Nur dass es sehr viel komplizierter ist, natürlich. Am Ende kriegt man aber eben etwas, dass sich – nach einem italienischen Mathematiker – der „Ricci-Krümmungstensor“ nennt. Und auf der anderen Seite der Gleichung steht der Energie-Impuls-Tensor, der beschreibt, wie viel Energie und Masse sich in einem bestimmten Punkt der Raumzeit befindet, beziehungsweise wie viel Energie und Masse durch diesen Punkt hindurch fließt. Das ganze Zeug im Universum ist ja dynamisch und das muss man berücksichtigen. Das ist jetzt alles enorm vereinfacht, aber im wesentlichen ist das das Herzstück von Einsteins Theorie: Eine Gleichung mit zwei Tensoren, einer beschreibt wie sich der Raum krümmt und der andere, wie viel Energie und Masse sich irgendwo befinden.

Eine Gleichung zu haben ist das eine. Sie zu lösen, das andere. Bei den Einsteinschen Feldgleichungen ist das alles andere als einfach. Aber wenn man sie löst, dann ist das Ergebnis eine Metrik. Also eine Funktion, die mir sagt, wie die Abstände in der Raumzeit berechnet werden. Und erinnern wir uns an den Anfang der Folge, als ich von der euklidischen Metrik und der Manhattan-Metrik erzählt habe. Je nachdem wie der Raum beschaffen ist – eine zweidimensionale Fläche oder ein Gitter aus Straßen – haben wir eine andere Metrik gebraucht. Im Umkehrschluss heißt das: Wenn ich die Metrik kenne, kann ich daraus ableiten, wie die Geometrie des Raumes aussieht, die sie beschreibt. Wenn ich also die Einsteinschen Feldgleichungen löse und eine Metrik finden kann, dann kann ich daraus die Geometrie der Raumzeit ableiten oder anders gesagt: Die Form des Universums.

Das war jetzt sehr viel, aber auch sehr notwendige Mathematik um die Frage zu beantworten: Welche Form hat das Universum denn jetzt? Die Antwort lautet: Kommt drauf an. Es kommt darauf an, welche Annahmen man über den Energie-Impuls-Tensor trifft. Wüssten wir exakt, wie viele Masse und Energie an welchen Punkten des Universums existiert, dann – ok, könnten wir die Gleichungen immer noch nicht lösen, weil das absurd komplex wäre. Aber das wissen wir ja sowieso nicht. Alle bisherigen Lösungen der Einsteinschen Gleichungen gehen von stark vereinfachten Annahmen aus. Man kann zum Beispiel voraussetzen, dass die gesamte Materie und Energie komplett gleichmäßig in allen Richtungen im Universum verteilt ist. Das ist etwas, was zumindest in grober Näherung für das Universum das wir beobachten, korrekt ist. Da gibt es keine Ecken, in denen absurd viel mehr Galaxien zu finden sind als anderswo. Und wir können voraussetzen, dass sich die Abstände im Laufe der Zeit ändern können. Auch das basiert auf Beobachtungsdaten, nämlich der Beobachtung der Expansion des Universums. Wenn wir damit probieren, die Einsteinschen Gleichungen zu lösen, kriegen wir etwas, was sich Friedmann–Lemaître–Robertson–Walker-Metrik nennt, nach den vier Wissenschaftlern, die genau das getan haben. Mit dieser Metrik kann man unser reales Universum halbwegs gut beschreiben; wir kriegen einen expandierenden Kosmos, können aber leider immer noch nichts über dessen genaue Form aussagen. Darüber habe ich in Folge 398 der Sternengeschichten genauer gesprochen. Solange wir nicht auch wissen wie VIEL Materie und Energie insgesamt im Universum ist, wissen wir nicht, wie es als ganzes insgesamt gekrümmt ist oder ob es überhaupt gekrümmt ist. Anders gesagt: Wir wissen nicht, ob es das vierdimensionale Äquivalent einer Kugel oder eines Blatt Papiers ist.

Wir könnten auch sagen, dass das Universum gar keine Materie enthält. Das ist zwar offensichtlich falsch, macht aber die Berechnung einfacher und dann kriegen wie eine De-Sitter-Metrik beziehungsweise einen De-Sitter-Kosmos. Das klingt zwar nach einer unnötigen mathematischen Übung, aber solche De-Sitter-Modellen waren in der Anfangszeit der Kosmologie wichtig, um überhaupt irgendwie zu verstehen, wie die Feldgleichungen funktionieren. Und tatsächlich war das Universum ganz zu Beginn ja vielleicht wirklich näherungsweise ein De-Sitter-Raum, es hat ja ein paar Sekundenbruchteile gebraucht, bis die Materie entstanden ist.

Es gibt noch jede Menge andere Metriken, zum Beispiel die Anti-De-Sitter-Metrik, die uns schon mal bei der Folge 538 über das holografische Universum. Oder die Gödel-Metrik aus Folge 354: Da hat der Mathematiker Kurt Gödel vorausgesetzt, dass das Universum als ganzes rotiert und am Ende eine Metrik rausbekommen, nach der Zeitreisen möglich sind. Aber wie gesagt: Nur weil man das ausrechnen kann, folgt daraus nicht, dass es auch so ist. Einsteins Gleichungen sind enorm mächtig. Sie können nicht nur ein Universum beschreiben, sondern jede Menge. Und wir müssen uns noch sehr viel länger mit der Metrik beschäftigen, wenn wir wissen wollen, welches davon unser eigenes ist.