Dieser Gastartikel ist ein Beitrag zum ScienceBlogs Blog-Schreibwettbewerb. Alle eingereichten Beiträge werden im Lauf des Septembers hier im Blog vorgestellt. Danach werden sie von einer Jury bewertet. Aber auch alle Leserinnen und Leser können mitmachen. Wie ihr eure Wertung abgeben könnt, erfahrt ihr hier.
Dieser Beitrag wurde von Alderamin eingereicht.
———————————————————————————————————————–
Die Größe des Universums
Die meisten Menschen werden gelernt haben, dass das Universum ziemlich groß ist. Man verwendet zur Entfernungsangabe nur selten eine Größe wie „Kilometer“, weil selbst im Sonnensystem die Entfernungsangaben in Kilometern sehr große Zahlen ergeben, die sich niemand vorstellen kann, und „Gigameter“ oder „Exameter“ helfen bei der Veranschaulichung auch nicht weiter, weil sie in der Erfahrungswelt nicht vorkommen. Die wenigsten werden sich daher eine Vorstellung davon machen können, wie gewaltig die Abgründe zwischen den Himmelskörpern sind. Im Folgenden möchte ich an ein paar Modellen versuchen, dem Leser eine Ahnung zu vermitteln, was sich hinter den “astronomisch“ großen Entfernungsangaben verbirgt.
Das Modell des Sonnensystems
Fangen wir mit einem handlichen Modell an, mit dem wir unsere Erfahrungswelt gerade noch ins Verhältnis zu astronomischen Entfernungen setzen können. Viele besitzen zu Hause einen Globus. Diese gibt es in verschiedenen Größen, wobei 30 cm Durchmesser eine typische Größe ist (ziemlich genau die lange Seite eines DINA4-Blattes). Dies entspricht einem Maßstab von 1:42.520.000, denn 42.520.000 mal 0,3 m sind 12.756.000 m, das ist der Erddurchmesser von Pol zu Pol (12756 km). Ein mm auf dem Globus entspricht demnach 42,52 km in der Realität. Das ist ein wenig mehr als ein Marathonlauf oder eine Sonntagnachmittags-Fahrradtour, also eine Strecke, die man buchstäblich erfahren kann. Diese Strecke kann man auf einem solchen Globus gerade noch erkennen.
Die Internationale Raumstation ISS würde diese Modellerde geradezu im Tiefflug in 1 cm Abstand umkreisen, wie auch die vielen anderen Satelliten in niedriger Erdumlaufbahn. Die geostationären Satelliten auf 35800 km Höhe umkreisten die Modellerde in fast exakt 1 m Abstand von deren Zentrum (42200 km).

Globus CC BY-SA 3.0 by Christian Fischer
Riesenrad CC-BY-SA-2.0-DE by Lung
Wie groß wäre der Mond in diesem Maßstab und wie weit wäre er entfernt? Er hat einen Durchmesser von 3480 km, das wären im Modell 8,2 cm, etwa die Größe eines Apfels oder einer Orange (die Orange ist passenderweise auch „verkratert“). Dieser orangengroße Mond würde die globusgroße Erde in 9 m Entfernung umkreisen, wobei er sich pro Tag ziemlich genau einen Meter auf seiner Bahn weiter bewegen würde, etwa 4,3 cm pro Stunde, 1,1 cm pro Viertelstunde. Ein Lichtstrahl wäre in diesem Maßstab hingegen mit 7 m/s oder rund 25 km/h unterwegs, ein zügiges Fahrradtempo. Entsprechend passiert ein von der Erde ausgesendeter Lichtstrahl den Mond nach 1,3 Sekunden. Wie lange braucht er bis zur Sonne?
Die Sonne ist in diesem Maßstab ganze 3,5 km entfernt eine Strecke, die von Astronomen „astronomische Einheit“, kurz AE (oder AU für Astronomical Unit) genannt wird. Ein Lichtstrahl braucht 8 Minuten 20 Sekunden für diese Entfernung, für die ein Verkehrsflieger mit 900 km/h theoretisch nonstop knapp 19 Jahre (!) benötigen würde.
Da uns Sonne und Mond am Himmel fast genau gleich groß erscheinen, die Sonne jedoch rund 400-mal weiter entfernt ist, muss die Sonne also etwa 400-mal größer als der Mond sein. Das sind dann 32,7 m Durchmesser. Die Größe eines Riesenrades oder eines 9-stöckigen Hochhauses. 109-mal der Durchmesser der Erde, die gegen die riesige Sonne nur ein unbedeutender Klecks ist, kleiner als viele ihrer Sonnenflecken. Auf die Entfernung der Sonne wäre die kleine Erde nicht mehr als Scheibchen mit bloßem Auge erkennbar, sie wäre von dort aus gesehen nur ein heller Stern, während die Sonne an unserem Himmel als Scheibe erscheint und wir ihre Hitze spüren. Was für eine gewaltige Energiemenge sie doch produziert!
Unsere globusgroße Modellerde umkreist die Modellsonne in einem Erdenjahr, wobei sie pro Tag etwa 60 m auf ihrer Bahn voran kommt, oder einen Millimeter in 1,45 Sekunden. Das könnte man gerade noch mit dem bloßen Auge erkennen. Ein Marathonlauf in 1,5 Sekunden.
Die Erde zählt mit Merkur, Venus und Mars zu den inneren Planeten im Sonnensystem, die sich alle innerhalb von maximal 5,8 km um die Modellsonne wiederfinden würden (Mars wäre mit 16 cm etwa so groß wie eine Honigmelone). Die äußeren Planeten im Sonnensystem sind teilweise erheblich weiter von der Sonne entfernt. Der helle Jupiter ist etwa fünf AE, also fünfmal soweit wie die Erde von der Sonne entfernt, das sind 17,5 km im Modell. Saturn wäre etwa 35 km (10 AE) entfernt und Neptun sogar gute 100 km (30 AE), von wo aus gesehen unsere Riesenrad-Sonne zu einem blendendhellen Punkt geschrumpft erschiene, nur 1/1000 so hell wie von der Erde, aber immer noch 300 mal heller als der Vollmond. Das fernste Objekt, das Menschen geschaffen haben, die Sonde Voyager 2, befände sich rund 400 km von der Modellsonne entfernt. Da wird unser Modell schon recht unhandlich. Die äußerste Grenze des Sonnensystems, die Oortsche Wolke, aus der die Kometen entstammen, wäre bis zu 350.000 km entfernt, also fast schon auf dem Mond. Man erinnere sich: 1 mm im Modell – 42,5 km in der Realität. Und das gesamte Sonnensystem bräuchte in diesem Modell die Umlaufbahn des Mondes! Und dies ist, kosmisch gesehen, gerade mal unser Vorgarten!
Das Fixsternmodell
Die Strecke zum nächsten Fixstern wäre fast eine Million km. Für die Welt der Fixsterne brauchen wir einen anderen Maßstab. Nehmen wir an, die Astronomische Einheit schrumpfte auf die Länge eines Millimeters. Die Sonne, unser Riesenrad von vorhin, schrumpfte auf einen knappen hundertstel Millimeter, so groß wie ein Partikel des Zementstaubs. Der Planet Jupiter umkreiste die Sonne in 5 mm Abstand, Neptun in 3 cm, Voyager 2 hätte 12 cm zurückgelegt und die Oortsche Wolke endete bei ca. 100 m. Zum nächsten Fixstern wären es dann 272 m. Im Schnitt fänden wir in der Sonnenumgebung in einer Kugel von 250 m Durchmesser einen staubpartikelgroßen Stern.
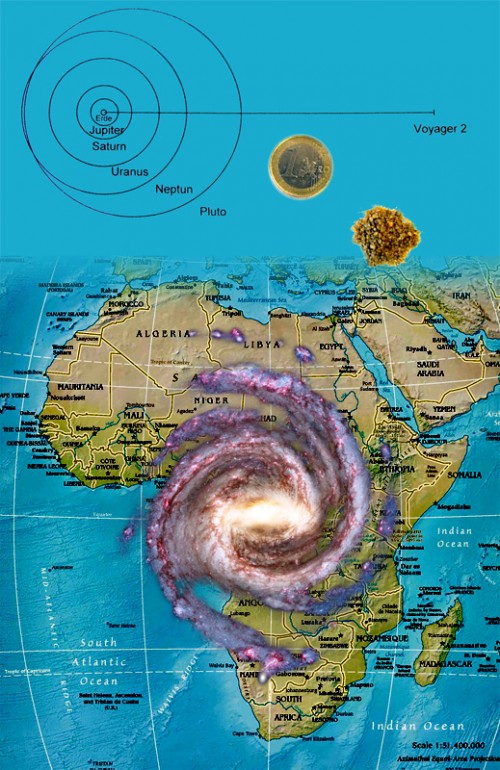
Afrikakarte PD
Milchstraßengalaxie PD by Nick Risinger
Fast alle für das bloße Auge sichtbaren Sterne liegen innerhalb von 1000 Lichtjahren entsprechend 62,5 km; die meisten der Sterne in diesem Umkreis sind aber viel zu lichtschwach, um überhaupt gesehen zu werden. Bereits der uns nächste Sterne, Proxima Centauri, ist ohne Teleskop nicht zu sehen, er ist nur ein hunderstel so hell wie die schwächsten, mit bloßem Auge noch sichtbaren Sterne. Ein paar helle Sterne in der Sonnenumgebung sind Sirius (8,6 LJ = 540 m), Wega im Sternbild Leier (25 LJ = 1500 m), Aldebaran im Stier (66,6 LJ = 4200 m), Beteigeuze im Orion (640 ± 150 LJ = 40 ± 9,4 km) und Deneb im Schwan (2600 ± 200 LJ = 162,5 ± 12,5 km; es gibt allerdings auch Messungen, die ihn bei nur ca. 1500 LJ Entfernung verorten). Deneb ist einer der absolut hellsten Sterne, 200.000-mal so hell wie unsere Sonne, weswegen er trotz seiner großen Entfernung am Himmel unter den hellsten zu finden ist. In unserem Modell wäre er ziemlich klein, nur etwa einen Millimeter im Durchmesser. Hingegen wäre Beteigeuze 6 bis 10 mm groß. Der Wert ist sehr unsicher, denn Beteigeuze hat keine klar definierte Oberfläche wie die Sonne, sondern verliert sich außen unregelmäßig geformt als dünnes Gas im Raum. Noch ein wenig größer, 13 mm, wäre der Stern VY Canis Majoris, der größte, den wir kennen. Er ist ca. 3900 LJ =250 km entfernt und knapp unsichtbar für das bloße Auge. Würde man ihn mit einem Verkehrsflugzeug umrunden wollen, das an einem Tag um die halbe Erde fliegt, bräuchte man dafür fast 800 Jahre!
Wir befinden uns hier immer noch in der Sonnenumgebung, alle diese Sterne liegen im gleichen Spiralarm der Milchstraße wie die Sonne. Die Milchstraße ist bekanntlich ein Spiralnebel, eine Welteninsel von 100.000 Lichtjahren Durchmesser, die geschätzt 300 Milliarden Sterne enthält. In unserem Modell hätte sie einen Durchmesser von über 6000 km und wäre damit etwas kleiner als der afrikanische Kontinent, der 8000 x7400 km misst. Im Zentrum wäre sie etwa 1000 km dick, in den Spiralarmen rund 200 km. Die Sonne kreiste in einem Abstand von rund 1700 km um das Zentrum (etwa die Strecke von Hamburg bis Rom) und würde sich pro Jahr ganze 46,5 mm auf ihrer Bahn um das Milchstraßenzentrum fortbewegen, das ist die Geschwindigkeit, mit der sich die arabische Kontinentalplatte aufgrund der Plattentektonik auf der Erdoberfläche bewegt. Ein Umlauf dauerte 230 Millionen Jahre.
Repräsentierten wir jeden Stern durch ein Sandkorn von mittlerem Durchmesser (0,5 mm), so bekäme man in einem Kubikmeter bei dichtester Packung (74% des Volumens mit Sandkörnern gefüllt) etwa 11,3 Milliarden von ihnen unter. Mit Sandkörnern der Anzahl der Sterne der Milchstraße könnte man ein Volumen von etwa 26,5 Kubikmetern füllen, ein Zimmer von 3 x 3,5 m mit 2,5 m Höhe. Tatsächlich wären die meisten unserer Modellsterne maßstabsgetreu viel kleiner; wir erwähnten bereits, dass die Sonne kaum einen hundertstel Millimeter durchmessen würde. Die meisten Sterne sind braune und rote Zwerge, die 1/2 bis 1/10 des Sonnendurchmessers haben; Zwergsterne wie die Sonne liegen zwischen 1/2 und 10 Sonnendurchmessern. Riesensterne mit einer Größe von100 Sonnendurchmessern und mehr sind hingegen extrem selten (nur 0,001% aller Sterne entfallen auf die hellen Riesen und Überriesen). Auf unser Modell verkleinert kämen wir damit gerade mal auf ein paar hundert Liter Volumen, im Wesentlichen dominiert durch die Klasse der Roten Riesen, die zwischen 20 und 100 Sonnenradien liegen; wenn ich diese mit einer mittleren Größe von 50 Sonnenradien ansetze, komme ich auf 400 Liter, knapp 3 Badewannen voll Sand. Verteilt auf ein Gebilde mit den Ausmaßen Afrikas wird klar, dass der Raum zwischen den Sternen sehr leer ist.
Die nächste größere Spiralgalaxie ist der Andromedanebel, der sich im Modell etwa 150.000 km entfernt auf halber Strecke zum Mond befände. Zeit, den Maßstab noch einmal zu wechseln.
Das Galaxienmodell
Wir verkleinern dazu ein Lichtjahr auf einen Millimeter. Das Sonnensystem mit der Oortschen Wolke als Grenze schrumpfte dann auf einen Radius von 1,6 mm, so dass sich die Astronomische Einheit auf 16 Nanometer (Millionstel Millimeter) und die Sonne auf 0,15 Nanometer, etwa der Größe von Natrium-Atomen, verkleinern würde. Voyager 2 hätte seit 1977 zwei tausendstel Millimeter zurück gelegt. Die meisten mit bloßem Auge sichtbaren Sterne fände man in einer 2 m durchmessenden Kugel um die Sonne vor, die das Milchstraßenzentrum in 27 m Entfernung umkreiste. Die Milchstraße schrumpfte mit 100 m Durchmesser auf die Größe eines Fußballfeldes (das allerdings schmaler ist), und wäre im ellipsoiden Zentrum etwa 16 m dick, in den Spiralarmen 3 m. In diesem Maßstab wäre der mittlere Sternabstand in der Sonnenumgebung rund 4 mm.

Messier 81 Galaxie PD HST image by NASA/ESA
Die nächsten Zwerggalaxien, die beiden Magellanschen Wolken wären 170 m (Große Magellansche Wolke) und 200 m (Kleine MW) entfernt und würden 14 bzw. 7 m durchmessen. Die nächsten größeren Galaxien wären der Andromedanebel (2,5 km entfernt und 140 m durchmessend) und der Triangulumnebel (2,8 km / 50 m). Der Andromedanebel (besser: sein helles Zentrum) ist gerade noch mit bloßem Auge zu erkennen. Das Licht, das man heute sieht, war 2,5 Millionen Jahre unterwegs zu uns. Es machte sich auf den Weg, als die ersten Urmenschen der Gattung Homo (Home rudolfensis) gerade aus den Australopithecus-Vormenschen entstanden (wer 2001 Odyssee im Weltall kennt, denke an die Eingangsszene).
Mit ca. 70 anderen, überwiegend zwergenhaften Galaxien bilden die oben genannten Galaxien die Lokale Gruppe, die etwa 7 bis 8 Millionen Lichtjahre, im Modell also 7 bis 8 km durchmisst. Die nächste Galaxiengruppe liegt im Sternbild Sculptor, das von Europa aus gesehen stets unter dem Horizont bleibt. Sie ist etwa 12 Millionen Lichtjahre, also 12 km im Modell, entfernt. Viele weitere Galaxien, die in den Teleskopen von Amateurastronomen zu sehen sind, fänden sich in einigen 10 km Entfernung. Der nächste große Galaxienhaufen liegt im Sternbild Jungfrau (Virgo; daher der Name Virgo-Galaxienhaufen), etwa 54 Millionen Lichtjahre (54 km) entfernt. Er enthält ca. 1300 bekannte Galaxien. Eine davon ist die bekannte Riesengalaxie Messier 87, die and die 1 Million Lichtjahre (1 km im Modell) durchmisst und rund 200-mal die Masse unserer Milchstraße hat.
Dieser Galaxienhaufen bildet das Zentrum einer noch größeren Struktur, des Virgo-Superhaufens, zu dem auch die Lokale Gruppe, die Sculptor-Gruppe und 100-200 andere Galaxienhaufen gehören. Der Virgo-Superhaufen durchmisst etwa 110 Millionen Lichtjahre (110 km im Modell) in der langen Achse und bildet eine flache, langgestreckte, elliptische Wolke, die am Rande eines großen Leeraumes (Void) liegt. Die Struktur des Universums im Großen besteht aus solchen Leerräumen von 30 bis 500 Millionen Lichtjahren Durchmesser (im Modell: 30-500 Kilometer), zwischen denen Filamente aus Galaxienhaufen wie in einem porösen Schwamm angeordnet sind. Wir sehen diese Struktur sich immer wiederholend bis in große Entfernungen fortgesetzt, die in Milliarden Lichtjahren (1000 km im Modell) gemessen werden.
Das Licht der fernsten nachgewiesenen Galaxien brauchte über 13 Milliarden Jahre zu uns, das entspricht fast dem Alter des Universums von 13,75 Milliarden Jahren. Da sich diese Galaxien inzwischen aufgrund der Expansion des Weltalls sehr viel weiter von unser entfernt haben, würde man ihre augenblickliche Entfernung an einem imaginären Maßband abgelesen mit rund 30 Milliarden Lichtjahren messen. In unserem Modell wären das 30000 km – größer als die Erde. Das beobachtbare Universum hätte im Modell einen heutigen Radius von 46000 bis 47000 km – etwas weiter als die Entfernung der geostationären Satelliten vom Mittelpunkt der Erde. Es enthält grob geschätzt 100 Milliarden Galaxien zu je 100 Milliarden Sternen, das sind 10^22 Sterne – eine 1 mit 22 Nullen. Wenn wir jeden Stern mit einem Sandkorn von 0,5 mm Durchmesser repräsentieren, so kämen wir auf etwa 1 Billion Kubikmeter = 1000 Kubikkilometer Sand – ein Würfel der Seitenlänge 10 km, höher als der Mount Everst, aber viel weniger als der Sand der Sahara (womit auch die Frage geklärt wäre, ob es mehr Sterne im Universum gibt, als Sandkörner auf der Erde – im beobachtbaren Universum bei weitem nicht).
Das beobachtbare Universum findet seine Grenze da, von wo das Licht während seiner Lebenszeit gerade noch die Distanz bis zu uns überbrücken konnte. Es ist dort jedoch höchstwahrscheinlich nicht zu Ende, sondern sehr viel größer. Wir wissen nicht, wie groß es insgesamt ist, es gibt nur Abschätzungen für eine Mindestgröße, die es keinesfalls unterschreitet – tatsächlich könnte es möglicherweise unendlich groß sein. Wenn es unendlich groß wäre, dann wäre es unvermeidlich, dass es in einer gewissen Entfernung eine exakte Kopie unseres beobachtbaren Universums gäbe, denn dieses befindet sich in einem von endlich vielen (10^10^122) möglichen Quantenzuständen aller seiner elementaren Volumenelemente; wenn unendlich viel Raum vorhanden ist, müssen sich mögliche Kombinationen zwangsläufig wiederholen, und zwar unendlich oft. Man kann abschätzen, dass dies in einer Entfernung der Größenordnung 10^10^100 m zu erwarten wäre. Das ist eine 1 mit 10^100 Nullen, wobei 10^100 bereits eine 1 mit 100 Nullen ist. Hier versagt jegliche Modellbildung. Unser Universum durchmisst etwa 10^30 Millimeter. Wenn wir 1 mm pro 0 benötigten, dann könnten wir im gesamten beobachtbaren Universum „nur“ 10^30 Nullen hintereinander schreiben. Das ist eine große Zahl, aber 10^100 ist 10^70-mal größer. Wenn wir das gesamte Volumen des beobachtbaren Universums mit 0en füllen würden und jede Null einen Kubikmillimeter bräuchte, dann fasste unser Universum 10^90 Nullen, und wir bräuchten immer noch 10 Milliarden beobachtbare Universen, um 10^100 Nullen unterzubringen. Und diese Zahl gäbe dann gerade mal an, wie viele Nullen die Strecke in Metern hat, d.h. wie oft man einen Meter mal 10 nehmen muss, bis sich unser Universum in exakter Kopie wiederholte. Und bei der ersten exakten Kopie wäre nicht Schluss, sondern es wäre die erste von unendlich vielen Wiederholungen.
Das Universum ist also in der Tat ein Ort mit sehr viel Platz. Die Annahme, es sei nur für uns geschaffen worden, erscheint da mehr als vermessen.

WOW!
Wow, das ist echt verdammt groß 😉
Der Artikel gefällt mir sehr gut, auch wenn beim zweiten Verkleinerungsschritt in meinem Geiste Schluss ist, man kann trotzdem erahnen wie groß und vor allem leer das Universum wirklich ist.
Wow scheint die nicht nur meine erste Reaktion zu sein 😉
Kreationisten steigen ja schon bei Zahlen größer als 6.000 aus.
Meine nicht. Meine Reaktion ist: DAMMIT!
Der hat meinen Artikel geklaut. Ich hatte echt noch von letztem Jahr einen Artikel im Fach (den ich Florian schon längst hätte schicken wollen – naja, zu spät is eben zu spät 🙁 ), der sich mit Entfernungsmaßstäben im Universum beschäftigt. Als Aufhänger diente mir da der altbekannte Enterprise-Spruch „Lichtjahre von der Erde entfernt dringt die ENTERPRISE dabei in Galaxien vor, die nie ein Mensch zuvor gesehen hat“ – der schön illustriert, wie wenig Menschen auch nur einen Hauch von Ahnung haben, wenn es um, äh, „kosmische Größenordnungen“ geht.
@Alderamin: schön jemacht. 🙂
@Sprtikopf
Wenn die Kreationisten recht hätten, könnte man gerade mal die Breite unseres Spiralarms überblicken, weil das Universum nicht alt genug wäre, dass Licht von entfernteren Orten zu uns dringen könnte. Die Kreationisten würden vermutlich darauf antworten, dass Gott natürlich auch die gesamten Photonen, die uns aus größeren Entfernungen erreichen, gleich mit dem All geschaffen habe, was Ihn dann allerdings zum größten Betrüger aller Zeiten machen würde.
@alle
Danke für die Wows, die waren das Ziel des Artikels (ich hab‘ beim Rechnen manchmal selbst gestaunt).
@Bullet
Tut mir leid 😉 Einen ähnlichen Artikel hatte ich seit 2010 bei „Gottlos Glücklich“ im Netz, aber die Seite gibt’s nicht mehr, den Artikeltext hatte ich auch nicht gesichert, so habe ich ihn (mit aktuellerem Wissen) from scratch neu geschrieben.
Am besten fand ich drei Badewannen Sand in Afrika 😉
Da kommt mir der Gedanke, dass wir das Universum schon aus dem Grund nie in seiner Gesamtheit begreifen können: Um diese Information zu speichern, bräuchten wir in unseren Gehirnen Platz für so viele Quantenzustände, wie das Universum selbst hat. (So einen dicken Kopf hatte ich nicht mal nach den schlimmsten Nächten.)
Trotzdem finde ich es interessant, dass das Universum an mindestens einer Stelle einen Punkt ausbildet, an dem es beginnt, ein grobes Abbild von sich selbst zu speichern. Warum tut es das?
@schlappohr
Falls das Universum unendlich groß ist (was nur eine Möglichkeit ist, es könnte auch endlich groß und abgeschlossen sein), bleibt ihm, mit einer großen, aber abzählbaren Zahl möglicher Zustände, ja nichts anderes übrig.
Wenn Du 7-mal einen Würfel wirfst, wird sich mindestens eine Seite mindestens einmal wiederholen. Immer dann, wenn ich mehr Zufallsversuche als mögliche Werte habe, gibt es zwangsläufig Wiederholungen von Werten.
Es wäre natürlich theoretisch denkbar, dass bei einem Zauberwürfel die Seite 1 nur einmal fällt und nie mehr auftritt, während sich nur andere Werte wiederholen. Ich sehe allerdings keinen Grund, eine so pathologische Verteilung von Quantenzuständen anzunehmen, sondern gehe davon aus, dass alle Zustände, die mindestens einmal vorkommen, eine nicht verschwindende Auftrittswahrscheinlichkeit haben und dann auch in unendlicher Wiederholung auftreten müssen.
Schön geschrieben, auch wenn ich gestehen muss, dass ich bei den größeren Modellen dann irgendwie doch nicht mehr ganz mitkomme. Die Nullen sind schon beeindruckend genug 😉
Zur Ergänzung:
Sternsandkörner: https://what-if.xkcd.com/83/
WOW! (Ja, ich weiß, das hatten wir schon … 🙂 )
Ich hatte ja schon angedeutet, das ich sehr gespannt auf diesen Artikel bin, und ich wurde nicht enttäuscht.
Ich hatte neulich eine sehr interessante Diskussion mit einem Kollegen, bei der es unter anderem auch um die Entfernungen in unserem Sonnensystem und unserer Milchstraße ging, hatte aber den Eindruck, das es für ihn nicht so ganz begreifbar war.
Ich bin sicher mit ein paar Eckdaten aus Deinem Artikel kommen wir der Sache ein ganzes Stück näher.
Bleibt mir nur noch Beifall zu klatschen … 🙂
@Alderamin
Ich glaube, wir reden von verschiedenen Dingen. Die Notwendigkeit der Wiederholung der Quantenzustäne in einem unendlich großen Universum ist mir schon klar (der selbe Grund, warum in einem genügend großen Computerspeicher Bitkombinationen mehrmals auftreten müssen)
Mit „ein grobes Abbild von sich selbst zu speichern“ meine ich etwas verklausuliert uns selbst. Wir haben ein grobes Abbild des Universums in unserer Vorstellung, sind aber gleichzeitig Teil des Universums. Warum existiert also in einem Teil des Universums eine solches Abbild? Ist vermutlich eher eine philosopische Frage.
@schlappohr
Warum tut es das?
Wir sind das Backup für den Stromausfall! Das erklärt einiges. Hoffentlich gibt es noch mehr Backups – so wie wir mit uns umgehen!
@Alderamin
WOW!
@Schlappohr
Selbstähnlichkeit? Ein Modelluniversum im Kopf ist halt eine Teilmenge der exp(10^122) Quantenzustände.
Wobei das Modell im Kopf aber auch nur ein extrem begrenztes ist. Wer kennt schon die Namen von mehr als einer handvoll Sterne? Und deren Eigenschaften? Und wie wenig von der Erde hat der Einzelne je gesehen?
Klasse Artikel und enorm informativ! Einige Passagen musste ich mehrfach lesen und bei den großen Skalen kann ich es mir auch nicht mehr vorstellen.
Besonders anschaulich finde ich einerseits die 19 Jahre Flugzeit, die ein normales Flugzeug zur Sonne unterwegs wäre (kann man sich irgendwie gut merken) und dann auch die drei Badewannen voll Sand (Sterne) verteilt auf Afrika.
Ich finde auch immer wieder überraschend (obwohl ich es eigentlich weiss) wie weit weg alleine schon die Oortsche Wolke ist.
Darf ich mich dem allgemeinen Wow anschließen?
(Ich würd aber gern eine der Badewannen voll Sand behalten. Gibt ja schon genug Sand in Afrika. 😉 )
Wie zu erwarten: Sehr schön. Du hast gute Maßstäbe, passende Beispiele und anschauliche Grafiken gewählt.
Gefällt mir.
Sehr, sehr, sehr (ich könnt auch WOW! schreiben) gut geschrieben. Anschaulich erklärt, ich krieg immer eine Gänsehaut, wenn ich versuche mir diese gigantischen Entfernungen vorzustellen. Meine Schwester z.B. will davon gar nichts wissen, weil ihr das Angst macht.
Die Badewannen merk ich mir!
@Alderamin
Ich würde das nicht nur auf ein einzelnes Gehirn beziehen, sondern auf die Gesamtheit unseres Wissens in Form von Büchern, Festplatten, Gedanken etc. Das ist natürlich immernoch sehr beschränkt, aber das Erstaunliche ist, dass dieses Abbild überhaupt existiert (eine Notwendigkeit dafür erschließt sich mir nicht so ohne weiteres) und dass es sich ständig verfeinert.
Danke für den Link übrigens, das werde ich mal in einer ruhigen Stunde lesen.
@ElSaxo
„Wir sind das Backup für den Stromausfall! “
Da wäre mal interessant, wie das Restoring abläuft, wenn der Saft wieder da ist.
@Ursula
Leg‘ Dich in einer mondlosen klaren Nacht an einem dunklen Ort auf eine Decke, einen Liegestuhl oder an einen Strand und blicke zum Sternenhimmel. Stelle Dir dabei vor, Du blicktest in einen tiefen Abgrund. Gruselt ein bisschen.
Gut, dass es die Schwerkraft der Erde gibt 🙂
Sehr guter Artikel mit anschaulichen Vergleichen! Äh, ich meine natürlich „WOW!“ 🙂
@Schlappohr
Zur Orientierung im Raum braucht ein Wesen mit Bewegungsfreiheit doch eine Art Landkarte im Kopf. Dass wir Menschen dabei etwas über das Ziel hinausgeschossen sind und Dinge kartographieren, die wir in absehbarer Zeit oder nie erreichen können, ist sicher unserer angeborenen Neugier geschuldet, und der Tatsache, dass wir uns instinktiv Marken zur Orientierung verschaffen. Man kann sich ja auch an den Sternen orientieren, was die Seefahrer vor Jahrhunderten stets taten (ihr Himmel hatte allerdings keine Tiefe).
Das schöne am Sternhimmel ist, wenn man ihn ein wenig kennt: man fühlt sich überall sofort zu Hause. Na ja, außer in Äquatornähe und südlich davon (jenseits des Äquators war ich noch nie, aber im Süden der Karibik einen auf dem über den Kopf gepurzelten Löwen zu sehen war schon ein wenig verwirrend, ganz abgesehen von den komischen Sternbildern im Süden).
Wie viel XLS Blätter (oder ähnliches) hast du für die ganzen Rechnungen benötigt ? 🙂
@Franz
Eins (für das Volumen der Sterne der Milchstraße). Den Rest habe ich mit dem Windows-Taschenrechner gerechnet. Viele Zahlen lassen sich aber auch dank der einfachen Maßstäbe AU oder Lichtjahre = Millimeter im Kopf umrechnen.
Ein toller Artikel, der mich unglaublich wütend macht, wütend das ich in diesem unermeßlich großem Universum gerade auf dem Planeten leben muss, deren einzig intelligente Bewohner sich liebend gerne deshalb gegenseitig abschlachten weil sie sich nicht einig werden können ob ihr Gottgesandter Prophet Nr.1 lieber Wasser in Wein verwandelt oder zugedröhnt mit brennenden Büschen in der Wüste gequaselt hat……
wenn ich jetzt noch bedenke, dass ich im zentrum des prinzipiell von mir einsehbaren universums bin, bekomme ich gleich einen grössenwahn… 🙂
btw: klasse artikel!
@Alderamin
Es gibt Kreationisten, die so argumentieren. Aber manche gehen durchaus davon aus, dass das Universum tatsächlich so groß ist, wie es ist und dass wir auch das echte Licht der Galaxien sehen. Deren Argumente lauten etwas anders:
1) Die Lichtgeschwindigkeit sei früher viel höher gewesen.
2) Die Erde befände sich in einem „gravitationellen Napf“, in dem die Zeit viel langsamer vergehen würde als außerhalb.
Das folgende Argument darf natürlich nicht fehlen:
3) Gott ist allmächtig und kann frei schalten und walten, weswegen er unbeeinträchtigt durch naturgesetzliche Beschränkungen das Sternenlicht der ersten Sterne viel schneller auf der Erde ankommen lassen konnte.
Siehe diesen Artikel bei Ken Hams „Answers in Genesis“
„Zur Orientierung im Raum braucht ein Wesen mit Bewegungsfreiheit doch eine Art Landkarte im Kopf. “
Aus unserer menschlichen Sichtweise heraus ist das alles nicht besonders aufregend. Aber im Grunde sind wir nichts anderes als eine Kombination von Quantenzuständen, die aus irgend einem Grund ein schwaches Abbild des Universums formen, während der Regolith auf dem Mond und das Vakuum ringsherum das nicht tun. Aus dieser abstrakten Sichtweise betrachtet finde ich das faszinierend.
„Das schöne am Sternhimmel ist, wenn man ihn ein wenig kennt:[…]“
Yep. Ich kann mich noch daran erinnern, dass ich mich mit 13 oder 14 zum ersten mal mit Sternkarten beschäftigt habe und dann in einer Novembernacht zu ersten mal Cassiopeia live gesehen habe (oder besser gesagt, sie erkannt habe). Das hat mich fast umgehauen. Seitdem ist sie für mich der Wegweiser am Himmel. Wenn man die rechte Seite des W als einen Pfeil betrachtet, dann zeigt dieser auf den Andromdanebel, usw.
Grossartig! Ich kenne Grössenvergleiche dieser Art für das Sonnensystem und habe sie auch bei sich bietenden Gelegenheiten benutzt. Aber unsere Galaxis und seine „nähere“ Umgebung bis hin zum ganzen Universum in dieser Form zu beschreiben, das ist einfach – WOW- !
Ein grosses Kompliment an den Autor!
@Alderamin zu #10:
Ähem. Willst du jetzt DEN Kardinalfehler in Statistik machen? 😉
Aber mal zurück zum Thema:
aufgrund der Notwendigkeit, so viele verschiedene Größenordnungsklassen verwalten zu müssen (rede ich jetzt von Distanzen zwischen Planeten oder von solchen zwischen Galaxienhaufen?) empfinde ich diese in Einheitsbrei-Massenmedien so häufig bis zum Erbrechen ausgelutschte Phrase „nach kosmischen Maßstäben nur ein Katzensprung“ so überflüssig und dumm. Denn fast immer verwenden die Journalisten diese dämliche Phrase komplett falsch – und ich behaupte,daß sie das bewußt falsch machen, um diese dämliche Phrase unterbringen zu können, weil sie sich in deren Gedankengebäude cool-wissend anhört. Das nervt schon etwas.
Würden sie aber bei ihrem „nur-ein-Katzensprung“-Vergleich noch die Größenordnungsklasse angeben müssen, könnte der interessierte Leser jeglichen Geschlechtes sofort den Blödsinn von hilfreicher Abschätzung erkennen. So aber gibt es fast immer eine Möglichkeit, diese dumme Phrase anzubringen und nie im wörtlichen Sinne falsch zu liegen.
@Bullet
#32
Was ist an der Aussage falsch, das verstehe ich nicht?
@All (und FF)
So viele interessante Artikel in so kurzer Zeit. … ich komm nicht nach !!!! 🙂
Ich hoffe ich bin nicht die Einzige, die sich bei den Vorstellungen ein bisschen gegruselt hat. Vor allem die 800 Jahre Flugzeit um VY Canis Majoris, brrrr, da ists mir kalt den Rücken runtergelaufen 😀 Auch wenn solche Modelle natürlich super sind und auch wirklich helfen, so RICHTIG vorstellen kann ich mir das Ganze trotzdem nicht in echt…mir wird dann höchstens schwindelig 😀
@Bullet, den Kardinalfehler sehe ich jetzt auch nicht….
Bsp1:gewürfelt 1-2-3-4-5-6-1=1doppelt
Bsp2:gewürfelt 1-1-2-2-3-3-4=1,2,3doppelt
Bsp3:gewürfelt 5-5-5-5-5-5-5=5doppelt(bzw sogar siebenfach)
Auch ohne mathematische Beweis ist keine Konstellation denkbar wo keine Zahl mindestens doppelt vorkommt.
Oder anschaulicher :du hast 6 obskisten und sollst dir 7 obst Stücke aussuchen, in eine wirst du wohl zwangsläufig
mindestens zwei mal greifen müssen. ..
Du hast nur die Richtung betrachtet in der es immer größer wird. In der anderen Richtung in der es immer kleiner wird ist es ähnlich seltsam.
Größenzunahme 10⁰m … 10¹m … 10²m … 10^n m
Größenabnahme 10⁰m … 10⁻¹ m … 10⁻²m … 10^-n m
Wir befinden uns in einem Bereich dieser Skala an dem unsere Wahrnehmung angepasst ist.
Wie würde der Raum aussehen wenn es möglich wäre eine Kamera zu bauen die in den Quantenraum schauen könnte. Das es dort sehr seltsam zu geht zeigt z.B. das Doppelspaltexperiment.
Danke für deinen Vortrag 🙂
https://www.youtube.com/watch?v=_PY5_j9sPCM
@Martin
Ich kenne mich halt mit dem Großen besser als als mit dem Kleinen.
Aber ich denke, mit dem Schauen wird’s im Kleinen zunehmend schwieriger, man muss ja immer kürzere Wellenlängen und somit Photonenenergien verwenden, um in die allerkleinsten Strukturen schauen zu können. Das ähnelte dann mehr einem „mit Tischtennisbällen im Dunklen um sich schmeißen und mit den zurückprallenden Bälle die Umgebung ertasten“.
Irgendwann sind da nur noch Felder, welche Teilchen (selbst auch wieder Felder) ablenken oder reflektieren. Einen profanen Gegenstand wie einen Tisch sehen wir ja auch nur deshalb, weil die Elektronen in den Hüllen der Tisch-Atome von einlaufenden elektromagnetischen Wechselfeldern in Schwingung gebracht werden und ihrerseits wie eine Antenne solche Schwingungen zurück senden. Dabei ist ein Atom eigentlich nur sehr viel Vakuum mit einem winzigen schweren Kern, der umgeben von den Feldern seiner nie zu lokalisierenden Elektronen ist. Und auch die Kernteilchen sind irgendwie leere Räume zwischen winzigen Quarks, welche ebensowenig greifbar sind. Und der weitaus größte Teil der Kernmasse steckt als Bindungsenergie in dem Vakuum zwischen den Teilchen. Eine für uns fremde Welt.
zu @Bullet #32
Schubfach- oder Taubenschlagprinzip
Aber dies gilt natürlich so nur im endlichen Fall ( bspw. die rationalen Zahlen lassen sich ja auf die natürlichen Zahlen verteilen ohne je eine doppelt zu belegen und dieses Spielchen kann ich ja sogar mit geraden und ungeraden Zahlen treiben…)…
zu @Alderamin #10
Mit Wahrscheinlichkeiten ist das so eine Sache – hier kann bestenfalls jeder Klasse „gleicher Zustände(/Zustandskonfigurationen)“ in ihrer Gesamtheit eine Wahrscheinlichkeit ( ≠ 0 ) zugeordnet werden, nicht jedem einzelnen auftreten einer „Zustands-Konfiguration“ außer sie käme nur endlich oft vor. „Mediocrity“ zieht da auch nur wenn es denn (hinreichende) Hinweise auf eine unendliche Wiederholung gäbe. Irgendwie ist aber die Existenz des beobachtbaren Universums ( daher Wahrscheilichkeit ≠ 0 für einen einzelnen Zustand) eher ein (mediokratischer) Hinweis in die andere Richtung -nur (endlich)*(Wahrscheinlichkeit des beobachteten Zustandes) erfüllt < ∞ .
So wie ich das sehe ist das Hauptproblem dieser Argumentation der Doppelgänger aus Wahrscheinlichkeitstheoretischen Betrachtungen in „einem unendlichen Universum“ ( etwas anderes ist es unendlich viele weitere separate Universen zu nehmen – vielleicht liegt da meine Verständnis-/Nachvollziehbarkeitslücke?)), dass $latex \int_V ZdP $ zwar ein lineares Funktional ist aber eben nicht linear in V(olumen). Solange sich das Universum ausdehnt und der beobachtbare Bereich wächst steigt ja auch die Zahl der „Elementarvolumina“ die für (diskrete, endlich viele) Quantenzustände zur Verfügung stehen und in ihrer Gesamtheit die zu replizierende „Kugel“ darstellen.
Ein wenig scheint mir das ähnlich zu “ Da ich immer nur endlich viele natürliche Zahlen „tatsächlich“ abzählen/explizit auflisten kann, kann ich auch in den ganzen natürlichen Zahlen nur endlich viele Summen bilden(und zwar lustiger Weise nicht mehr als ich Zahlen auflisten kann)“.
@StefanL
Warum nicht? Wir haben 10^10^122 mögliche Zustände, das ist eine endliche, abzählbare Menge. Da kann ich doch jedem Element eine Wahrscheinlichkeit zuordnen. Es müssen nicht alle eine Wahrscheinlichkeit > 0 haben (wenn sie in unendlicher Wiederholung nur endlich oft auftreten, also fast unmöglich sind). Gilt aber umgekehrt, dass ihre Wahrscheinlichkeit > 0 ist, dann treten sie notwendigerweise in unendlicher Wiederholung unendlich oft auf.
Vermutlich werden nicht alle möglichen Kombinationen von Quantenzuständen natürlich auftreten können, denn z.B. der Zustand unseres Universums ist ja (höchstwahrscheinlich) nicht einfach aus dem Nichts entstanden, sondern hat sich aus einem Anfangszustand gemäß gewisser Gesetzmäßigkeiten entwickelt, und nicht jeder Zustand muss auf diese Weise auch erreichbar sein. D.h. die denkbaren Quantenzustände sind gewiss nicht gleichverteilt.
Natürlich wäre es theoretisch denkbar, dass einige Zustände nur endlich oft auftreten, z.B. unser konkretes beobachtbares Universum. Eine solche Verteilung würde ich aber „pathologisch“ nennen. Das Universum fing großräumig in einem homogenen Zustand mit nur winzigen Temperaturunterschieden an und entwickelte sich zu dem, was es heute ist. Ich wüsste nicht, warum bei einer abzählbaren Menge von Zuständen und mindestens einer gegebenen Inkarnation eines bestimmten Zustands dieser fast unmöglich sein sollte.
Für mich steht der Sieger hiermit fest . Das ist so gut geschrieben, dass es eigentlich extremssssst unfair gegenüber den anderen ist 😀
Boah, jetzt ist mir etwas schwindelig …
Sehr geiler Artikel, Alderamin. Es gibt ja viele Ansätze, diese Größenverhältnisse darzustellen (das weiter oben verlinkte Video ist auch sehr gut), aber längst nicht alle Vergleiche gelingen, und dieser Artikel gehört zum Besten was ich in dem Bereich gesehen habe. Den werd ich bestimmt immer mal verlinken.
Den find ich auch gut, merk ich mir : )
grz
Dampier
@emreee
Hilfe, so viel Lob… erst mal Heuwägelchen. Ich hatte eigentlich fest damit gerechnet, dass sich viele über die Menge der Zahlen beschweren würden – wie in dem alten Witz, wo der Patient in der Anstalt seinen Mitinsassen immer seine Romane andrehen will, und als Kritik stets „bisschen viele Personen und bisschen wenig Handlung“ zu hören bekommt – bis der Anstaltswärter herausfindet, wer immer die Telefonbücher klaut…
Freut mich jedenfalls, wenn’s gut ankommt. Mein Favorit wäre aber ein anderer Artikel (ich verrate aber noch nicht, wer).
@Alderamin
Nö, wenn das so wie hier aufgezogen wird, machen die Zahlen sogar Spaß :-). Immer mit rotem Faden und anschaulichen Modellen – echt gut gelungen!
Hast du schon mal überlegt, öfter mal den einen oder anderen Blogartikel zu schreiben?
@tina
Zeit, tina, Zeit,…
Aber eine kleine Artikelreihe zum Thema „Mein erstes Teleskop“ hier bei Florian habe ich ja schon angekündigt. Da fehlen noch die Bilder und der (bis jetzt) Riesenartikel muss noch passend zerteilt werden. Wäre dann vielleicht was für die Zeit vor Weihnachten.
Bei so viel aufmunterndem Feedback bekomme ich Lust, vielleicht hin und wieder mal was zu schreiben. Ich würde ja sogar mal ein Buch schreiben, aber die Zeit…
@Alderamin
„Toll geschrieben und schön bebildert. Ein Kandidat für den Sieg“. Das Kompliment von Dir kann ich nur an Dich zurück geben. Ein grandioser Text.
Man wird wieder richtig demütig, wenn man sich klar macht, wie klein und unbedeutend unser Planet doch ist.
@Alderamin
Ja, so ein Tag müsste einfach ein paar Stunden mehr haben. Vielleicht lässt sich die Erde ja dazu überreden, etwas langsamer zu rotieren… (ein ganz superkleines bißchen langsamer wird sie ja schon jeden Tag).
Tolle Vergleiche. Schade, dass man sich nicht alle gleichzeitig merken kann, um „besserzuwissen“ 😉
Am besten haben mir die Nullen gefallen. 10 Milliarden Universen, gefüllt mit millimetergroßen Nullen – das dürfte die größte Zahl sein, die ich mir je im Leben vorgestellt habe (bzw. vergeblich versucht habe, vorzustellen).
@Alderamin
Moment:
$latex p\not= 0 \Rightarrow p\cdot\infty = \infty$ und das macht als Wahrscheinlichkeit keinen Sinn.
Und
Auch hier wieder: wenn eine einzelne explizite Zustandskonfigurationsmanifestation(Enklave) eine Wahrscheinlichkeit ≠ 0 hat und unendlich oft vorkommt ist die Gesamtwahrscheinlichkeit aller Vorkommen dieser speziellen Konfiguration nicht definiert ( = ∞ ) und so ist mein
zu verstehen. Nur der (Äquivalenz-)Klasse eines ( sich beliebig oft wiederholenden eindeutig bestimmten) Zustandes kann eine Wahrscheinlichkeit ( ≠ 0 ) zugeordnet werden wenn in der Klasse mehr als( egal ob abzählbar oder nicht) endlich viele „Kopien“ liegen.( Dein „ Wahrscheinlichkeit > 0 ist, dann treten sie notwendigerweise… unendlich oft auf“ könnte dem entsprechen wenn die angesprochene Wahrscheinlichkeit die Wahrscheinlichkeit der „unendlich oft Auftreten“(des bezeichneten Zustandes) ist).
Wenn nur endlich viele Elemente/Enklaven/Kopien in einer solchen „Gleichheitsklasse“ liegen kann natürlich die „Klassenwahrscheinlichkeit“ (gleichmäßig) auf die Elemente der Klasse „verteilt“ werden. Warum sollten diese endlichen Klassen Nullmengen sein (fast unmöglich)? So wie ich das sehe bedingt eine „vernünftige“ σ-Algebra das nicht notwendig, eher im Gegenteil, da wir nur endlich viele Klassen haben.
Für die exp( 10^122) möglichen Zustände heißt das bspw. bei Gleichverteilung, dass die Wahrscheinlichkeit irgendeine Enklave in einem bestimmten Zustand zu „treffen“ zwar 1/ exp(10^122) ist aber wenn es unendlich viele solcher Enklaven( Replikationen des beobachtbaren Universums ) gibt, da dann eine bestimmte( einen „ausgezeichneten“ Repräsentanten der Klasse) zu treffen, dafür ist die Wahrscheinlichkeit 0. Alternativ bliebe doch nur eine Nullmenge von Enklaven ( im W-Raum aller Enklaven) bei denen das nicht so sein mag. Ein äußerst schwaches W-theoretisches Argument für eine unendliche Wiederholung eines Zustandes( abgesehen davon warum sollten bestimmte Elemente einer solchen Klasse eine andere Wahrscheinlichkeit haben als die anderen( gleichen!) Elemente in der Klasse?) – d.h. fast sicher/unmöglich zieht überhaupt nicht (schon), da die Wahrscheinlichkeit einer solchen Nullmenge eben Null ist.
Auch sehe ich nicht wie da die (Wahrscheinlichkeits-)Argumente (für unendlich viele Kopien in einem Universum) mit der Ausdehnung (Zuwachs an Elementarvolumina) des Universums zusammenpassen sollen. Die Anzahl möglicher Zustände beziehen sich doch auf ein festes Bezugsvolumen( oder unterliege ich da einem Irrtum?) – andernfalls wären die exp(10^122) Zustände ja auch schon beim Urknall gegeben und ich denke nicht, dass die räumliche Anordnung( hier ganz konkret die Anzahl von Elementarvolumina zwischen zwei manifestierten Quantenzuständen) belanglos für die Gesamtanzahl von möglichen (zu kopierenden) Zuständen/Konfigurationen ist(?).
Toller Text!
Sehr schön und sehr kreativ bei den gewählten Veranschaulichungen 🙂
Cool! Echt coooool – das hat noch keine gesagt, den Rest durchaus 😀
Was für geniale Vergleiche …
und allmählich komme ich auch nicht mehr mit dem Lesen nach. Super, dieser Wettbewerb.
PS:
Kann es sein, dass @Bullet sich nicht mehr gemeldet hat, weil der seit gestern mit Würfeln spielt … ?
🙂
@Theres:
„Super, dieser Wettbewerb.“
Jep! Hätte ich nicht gedacht, dass wir soviele tolle Texte zu lesen kriegen!
(Und ich ärgere mich immer noch die Platte, dass ich meinen nicht mehr fertig gekriegt hab …)
„Faszinierend!“ Wie ein gewisser Wissenschaftsoffizier sagen würde 🙂
@ الذراع اليمين , bzw. α Cep, bzw. Alderamin:
Ich muss sagen: Der Artikel gefällt mir!
Auch falls ich was wiederhole, aber die Vergleiche sind gut. In meinem Bekanntenkreis werde ich ja hin und wieder mal für tolle Vergleiche gelobt, aber ich glaube, Du bist besser. Die Bilder sind auch schön montiert, also alles in allem würde ich sagen, Du hättest auch Lehrer werden können. 🙂 Du kannst jedenfalls hervoragend erklären, was man ja auch in Deinen Kommentaren immer wieder sieht.
—
Ach ja, den kann ich mir jetzt doch nicht verkneifen:
Sowas Dummes aber auch! – Dann laufen Deine Links aus der Religionsdiskussion vom vergangenen Jahr ja jetzt ins Leere. Ausser man findet sie im Web-Archiv wieder. Nun ja, kann mir ja letztlich egal sein, ob die Seite weiter existiert oder nicht. Die zwei oder drei Artikel auf die Du mich hingewiesen hast, liegen auch auf meiner Festplatte… – Bliebe blos die Frage zu klären, ob ich dazu noch mal was schreibe? – Antwort: Irgendwann vielleicht mal. 😉
@PDP10, #56:
Naja, vielleicht wiederholt Florian die Aktion ja in nächsten Jahr.- Dann kannst Du ihn immer noch einreichen. 😉
@Hans: „Naja, vielleicht wiederholt Florian die Aktion ja in nächsten Jahr.“
Kann gut sein. Kommt aufs Feedback drauf an.
@Hans
@PDP10
Vielleicht früher? Ich hoffe ja auf einige Folgeartikel, damit unser Autor in Ruhe seine Büchers schreiben kann. So, jetzt muss ich aber ins Bett … und beim Wettbewerb streike ich. Ich kann ja nicht bis auf vier alle aufschreiben … obwohl die Favoriten …
Sorry, ich kann mich dem allgemeinen Lob nicht anschließen. Abstraktes wird mit Abstraktem erklärt, das hilft einer echten Vorstellbarkeit nicht wesentlich weiter. Es liegt nicht an der (sachlich einwandfreien) Darstellung sondern an der Begrenztheit der sprachlichen Möglichkeiten überhaupt.
Die Videos und Grafiken veranschaulichen die Größenverhältnisse weitaus besser.
@Alderamin:
Wie immer, brilliant anschaulich erklärt. Vielen Dank dafür !
Klasse Artikel, dem Feedback schließe ich mich an! Eine Frage habe ich:
Das wäre ja dann „nur“ ungefähr die Entfernung des 1,5 fachen Milchstraßendurchmessers. Also nicht neben an, sondern eher am gemeinsamen Küchentisch… Wie stark ist hier der gravitative Einfluss der vergleichsweise großen Milchstraße auf die kleinen Nachbarn?
@myself (#32):
ich rette mich hiermit vor der argumentatorischen Niederlage durch den Kunstgriff der Kantenstellung, deren Wahrscheinlichkeit >0 ist. Und beim nächsten Mal lese ich sorgfältig alle Worte, die „mindestens“ heißen und verstehe sie auch korrekt. Wenn nicht, hol ich die Eckstellung aus der Kiste. 🙂
@StefanL
So rechnet man ja auch nicht. Man kann z.B. über die relative Häufigkeit der einzelnen Augenzahlen einen Grenzübergang gegen unendlich bilden, und dann kommt natürlich wegen der Gleichverteilung 1/6 pro Seite heraus. Da gibt es auf jeden Fall eine stationäre Verteilung.
Verstehe ich nicht. Wenn ich eine unendliche Menge von Würfeln mit zufälligen Ausrichtungen in der Ebene verteile, wieso sollte die Wahrscheinlichkeit 0 sein, die Augenzahl 6 zu treffen, wenn ich zufällig einen davon aufhebe? Wenn ich eine überabzählbare Zustandsmenge hätte, dann wäre dem so, aber exp(10^122) ist endlich.
Bei endlichen Markoffketten gibt es genau dann eine stationäre Verteilung, wenn diese ergodisch sind, also aperiodisch und positiv rekurrent (jeder Zustand wird mit endlichem Erwartungswert wieder erreicht).
Wenn ich z.B. den Würfelwurf als Markoffkette darstelle, dann habe ich 6 vollvermaschte Zustände mit Kanten, die alle 1/6 Übergangswahrscheinlichkeit haben. Damit ist Ergodizität erfüllt und es gibt eine stationäre Verteilung.
Worum es hier geht, ist: angenommen das beobachtbare Weltall ließe sich als Markoffkette modellieren mit den möglichen Kombinationen von Quantenzuständen als erreichbaren Markoff-Zuständen, deren Übergangswahrscheinlichkeiten durch die Physik gegeben sind. Da kann man die Expansion gleich mit einarbeiten, indem man mit jedem Schritt mehr Folgezustände einbaut. Wir starten in einem der Zustände geringer Entropie nach dem Urknall und führen eine endliche Zahl n von Übergängen durch (entsprechend dem aktuellen Alter des Universums, gemessen in Plankzeiten). Gibt es für die in n Schritten erreichbaren Zustände eine Wahrscheinlichkeitsverteilung?
Das ist nicht die stationäre Verteilung, die hier gesucht wird (die Markoffkette wird nicht einmal endlich sein, wenn das Weltall ewig wächst, und schon gar nicht positiv rekurrent, denn der Urknall kommt nicht wieder). Sondern die n-Schritt-Erreichbarkeit. Ich denke, diese Verteilung müsste in jedem Fall existieren, für jeden Zustand.
Die Werte für die Zahl der Zustände und den Erwartungswert des Abstands für eine Wiederholung nicht von mir, sondern aus Brian Greenes Buch „The Hidden Universe“. Leider war’s am Ende bei der Einreichung etwas eng, sonst hätte ich noch einen Haufen Links und Referenzen auf meine Quellen gesetzt.
@Thomas
Riesig 🙂 ( wobei Gravitation ja bidirektional ist.)
Die Magellanschen Wolken sind Satelliten der Galaxis.
Im Prinzip reicht das Newtonsche Gravitationsgesetz, großzügige Abschätzungen, die Sonnenmassen und Entfernungen ( LJ) umgerechnet → F~ 10^34 N
@Hans
Tja, leider. Und informiert wurde ich auch nicht. War wohl am Ende zu wenig los, zu wenige Querverweise, wir haben die Seiten auch nicht mehr richtig gepflegt. Es gibt aber auch viele andere gute Seiten, z.B. diese.
Zu dem Thema ist schon ziemlich alles gesagt. Mehrfach.
@Thomas
Sehr groß. Die Milchstraße zieht bereits Materie aus den Magellanschen Wolken und verzerrt deren Form. Wahrscheinlich wird sie diese auch irgendwann verschlucken, wie sie es mit vielen anderen Zwerggalaxien schon getan hat. Man geht davon aus, dass große Spiralgalaxien durch das Verschlucken von Zwerggalaxien zu ihrer heutigen Größe gewachsen sind.
@Alderamin
Ja, das ist aber nicht
sondern genau die angesprochene Klassenbildung: Die Wahrscheinlichkeit einen Bereich im (unendlichen) Universum zu treffen der genau einem bestimmten Zustand entspricht, aber nicht genau einen bestimmten all dieser (möglicherweise unendlich vielen) Bereiche die sich in diesem Zustand befinden. Welchen Grund gibt es denn in der zugrundegelegten σ-Algebra den „endlichen“ Elementen stets ein Maß=0 zuzuweisen?
Um Dein Würfelbeispiel aufzugreifen: Ja die Wahrscheinlichkeit einen( unter unendlich vielen) Würfeln zu greifen der (bspw.) die 6 zeigt ist 1/6 aber genau diesen Würfel ( unter den unendlich vielen die 6 zeigen – der Klasse die 6 zeigt) zu greifen ist 0. Jetzt deutlicher worin ich den Unterschied sehe?
Was Du mit Ergodizität willst ist mir nicht klar. Was soll denn der Erwartungswert der exp(10^122) Zustände sein, auf den sich das Universum stationär „einschwingen“ soll? Und was soll uns das dann in Bezug auf „Wiederholung/Kopie“ sagen?
Mein „Problem“ ist nicht zu einem definierten Zeitpunkt n Zustände haben zu können, sondern warum aus diesem lokal-temporären, statischem Zustandsraum(endlich) sich der „universale Gesamtzustand“(unendlich) ergeben soll. Wie Du selbst bemerkst:
Also ein ( mehr oder wenig stetiges) Anwachsen der Zustands(klassen)anzahl n. Nachvollziehbarer erscheint mir da Hugh Everetts Viele Welten so, das sich jeder mögliche Folgezustand einstellt. Aber welches ist das Kernargument, das sich tatsächlich identische Kopien im selben Universum befinden sollen ( bei Everett könnten ja wenigstens noch unterschiedliche Zustände wieder in gleiche Zustände übergehen…)?
Auch hier – Ja; aber eine Wahrscheinlichkeit für die n-Schritt-Erreichbarkeit ist doch kein Argument für die unendlich ofte Wiederholung des Zustandes(insbesondere ohne Rekurrenz)…oder was entgeht mir da? Einfach statischer (unendlicher) Hintergrund /Blockuniversums Hypothese? Ohne unendlich viele Urknalle (im selben Universum)?
Wie gesagt, zu einem gewissen Zeitpunkt n mögliche Zustände zu haben ( in einem beobachtbaren, endlichen Bereich) und daraus zu folgern, das für ein( wir sprechen hier ja nicht von Multiversum/Viele Welten) unendliches Universum, bei gleichzeitigem Anwachsen der Möglichkeiten im zeitlichen Verlauf, zwangsweise unendlich viele Kopien existieren, scheint mir irgendwie eine „Milchmädchen“ Rechnung ( Schubfachprinzip(endlich) im Unendlichen).
P.S.: Die drei Badewannen Sand über Afrika werden sicherlich im Gedächnis bleiben 😉 ;
@StefanL
Ok, hast Recht, diese Formulierung war so nicht korrekt, weil sie alle Zustände als rekurrent bezeichnet, was sicher nicht der Fall ist.
Jetzt verstehe ich erst Deine Klassenbildung. Für mich sind gleiche Zustände natürlich ununterscheidbar (selbst wenn sie an verschiedenen Orten lägen). So wie zwei 6en bei den Würfeln ununterscheidbar sind. Und da nehme ich halt an, dass ein erreichbarer Zustand (bzw. diese Klasse) bei einer unendlichen Menge von Versuchen (an verschiedenen Orten des unendlichen Universums) aus einem vergleichbaren Startzustand auch unendlich oft erreicht wird (jede Klasse hat unendlich viele Elemente).
War nur als kleiner Exkurs gedacht wegen der Würfel. Mir ist erst während des Schreibens klar geworden, dass es nicht um die stationäre Verteilung, sondern die n-Schritt-Erreichbarkeit geht. Aber die Ergodizität passte noch zum Würfelversuch, also ließ ich sie drin.
Es ist aber klar, dass man für ein unendlich großes Universum mit einem unendlich großen Raum zur Zeit des Urknalls anfängt, oder? Aus jedem Punkt (besser: aus einem minimalen Anfangsvolumen) wird dann in n Planckzeiten ein anderes, benachbartes beobachtbares Universum (das beobachtbare Universum ist einfach der Horizont, den man um einen fiktiven Beobachter zieht, der seine Grenze da hat, wo die Lichtlaufzeit das Alter des Universums erreicht – weiter sehen kann der Beobachter nicht; ganz wie der Horizont von Bord eines Schiffes aus gesehen, der seinen Rand an der Erdkrümmung findet).
Eben das Schubladenprinzip. Jedes Volumen eines beobachtbaren Universums ist eine Schublade mit einem bestimmten Inhalt. Deren gibt es unendlich viele, als mehr, als es Möglichkeiten gibt, die Schubladen zu füllen. Also findet man Schubladen mit gleichem Inhalt.
Ein simultaner Urknall im unendlichen Raum, das ist gleichbedeutend mit unendlich vielen Urknallen in jeweils allen beobachtbaren Universen. Wie das geht, steht hier. Oder alternativ zwei unendlich große Membranen, die überall gleichzeitig zusammenstoßen.
Dass es mathematisch möglich wäre, dass genau ein bestimmter Ort sich anders als alle unendlich vielen anderen entwickelt, mag zwar sein, ist aber physikalisch einfach nicht plausibel. Genauso wenig wie, dass alle außer einem Stein auf den Boden fallen, wenn man sie loslässt.
Sorry, ich kann’s besser nicht erklären (und die Idee ist sowieso nicht von mir, wie ich schon sagte…)
ich bin nicht kompetent um mit zu diskutieren,deswegen nur eine Verständnisfrage: kann etwas in endlicher Zeit unendlich werden, wenn es zu bestimmter Zeit (Urknall) entstanden ist. denn meines Wissens behauptet Alan Guth die Kosmosgeburt aus den Nichts vor 14 10^9 Jahren
und dann noch: diese deterministische Zahl von 10^10^122 Quantenzuständen mit der Kombinatorik betrieben wird ist doch in der Natur unbestimmt einmal wegen Heisenberg und zum Anderen weil es per Definition in der Natur Unbestimmtheiten gibt z.B den radioaktiven Zerfall
Es sollen keine Behauptungen, sondern Laienfragen sein
..nice … alles andere wäre auch absurd. (für alderamin)
habe schon etliche grössenvergleiche gesehen/ gelesen – dies ist ein sehr schöner darunter!
aber ich habe schon antworten von dir gelesen, die 10,5x grossartiger waren 🙂
nichtsumsoweniger: du sprichst von einem 13,75mrd Jahren alten Universum, meine letzte info war 13,819 (keine ahnung… planck o.ä.) – klär mich auf!
lg
#67, Alderamin
Irgendwie verwundert es mich ja schon, dass Du ausgerechnet darauf was zurück schreibst, aber zu dem Teil davor nicht. Nun gut, dann kann ich es mir sparen und es bleibt bei der Feststellung, dass wir in diesen Fragen unterschiedliche Meinungen vertreten, die sich nicht miteinander in Einklang bringen lassen. Halten wir es also mit dem alten Fritz: „Jeder solle nach seiner Façon seelig werden.“ – Amen. 😉
—
#62 Florian Freistetter
Ah ja. Also nach meinem subjektiven Eindruck scheint die Aktion bisher ja recht erfolgreich zu sein.
@Bruno
Ja, nach Planck-Messungen sind es 13,82 Milliarden Jahre. Hatte eine ältere Zahl von WMAP oder so im Kopf, muss mich erst an die aktuellen Werte gewöhnen 😉
@Hans
Öh, danke für das Lob über den Artikel 😳
Was das andere betrifft, es ist klar, dass wir da verschiedener Meinung sind, und haben da ja auch schon ausgiebig drüber diskutiert. Ich beantworte Dir aber gerne Fragen zu den Artikeln, wenn Du welche hast. Ich glaube nur nicht, dass einer von uns seine Meinung ändern würde. Belassen wir’s doch dabei (mir ist ja auch Wurst, was andere glauben, wenn sie damit glücklich sind, solange man mir das gleiche zugesteht).
So, jetzt bin ich erst mal eine Weile weg. Mal schauen, vielleicht gibt es da funktionierendes Internet. Falls noch Fragen kommen. Ansonsten spätestens bis 3. Oktober!
@Kalli
Du bekommst aber noch Antwort:
Nein, in endlicher Zeit kann etwas Endliches nicht unendlich werden. Deswegen schrub ich an StefanL ja auch, dass bei einem unendlichen Universum dieses schon zur Zeit der Entstehung unendlich groß gewesen sein muss (siehe auch den Link in #70 unter dem „hier“ im drittletzten Absatz: im sogenannten Blasenuniversum kann das Weltall unendlich groß angefangen haben, wenn in ihm eine andere Zeitachse gilt, als außen drumherum). Anders für das beobachtbare Universum (also den Teil, den wir von hier aus überblicken können): das war stets endlich und ist es heute noch. Deswegen ist diese „Schublade“ ja auch winzig klein in einem unendlichen Universum.
Trotzdem gibt es eine endliche Zahl möglicher Zustände, z.B. können die Elektronen im Atom ja nur bestimmte Werte annehmen, auch wenn etwa der Zeitpunkt eines Quantensprungs (Photonenemmission) unbestimmt und nicht vorhersagbar ist (wie auch bei der Radioaktivität, wo ähnliches für den Kern gilt). Ich weiß nicht genau, welche abzählbaren Zustände da den (vermutlich) Planck-Volumina zugebilligt werden, aber in einer Quanten-Welt ist halt alles irgendwie gequantelt. Kleiner als die Planck-Länge und Planck-Zeit geht es nicht.
@ Alderamin
besten Dank
Danke an den Verfasser. Manche meiner Probleme werden plötzlich sehr unbedeutend. Dieser Artikel ist der verschriftlichte „Totale Durchblicksstrudel“. Nur Ken Ham kann ihn unbeschadet lesen, weil er wie Zaphod Beeblebrox der Mittelpunkt seines eigenen albernen Universums ist.
Toller Artikel! Um es mit den Worten von Bender zu sagen: „Come on, universe, you big, mostly empty wuss!“
[…] Wäre die Milchstraße so groß wie der Kontinent Afrika, würden alle Sterne in ihr in zwei bis drei Badewannen passen. Da schwirrt mir der Kopf! Die Größe des Universums […]
Bei solchen Argumenten läuft vor meinem Geistigen Auge ein Film ab wie die Southpark Figur von Einstein (oder Newton etc) mit Occam’s Razor die Horden von irrationalen Argumenten bekämpft. Also im Prinzip eine Mischung aus Southpark, Texas Chainsaw Massacre und Braindead.
Grosse Klasse! Diesen Text musste ich mir ein paar Mal zu Gemüte führen, um all die Vergleiche und Modelle wenigstens im Ansatz zu verstehen.
Der Autor jongliert gekonnt und mit unaufdringlichem Witz mit all den verschiedenen Grössenangaben, dass einen Angst und Taumel erfassen könnte, und bewahrt den Leser am Ende zum Glück vor dem Fall in die Unendlichkeit.
Grossartig!
Auch von meiner Seite erstmal ein aufrichtiges WOW.
Was ich bei solchen Vergleichen dann immer interessant finde ist, dass die Gravitation selbst über diese rießen Distanzen immer noch wirkt. Wirklich „faszinierend“….
[…] Die Größe des Universums […]
[…] Interessantes zu sagen haben, dass es schade ist, dass sie das nicht tun. Hier hebe ich besonders den letztjährigen Siegerbeitrag von Alderamin […]
Den Text den ich eben erst gesehen habe, der hat mich nachdenklich gemacht. Kann bitte jemand nachrechnen ob die folgende Rechnung so stimmt?
Falls man das sichtbare Universum von 93 Mrd Lj auf den Erddurchmesser von 12700 km verkleinern würde, dann wäre im gleichen Maßstab die Milchstraße eine Art riesige Tischplatte mit ca 140 Metern Durchmesser.
Kann man das so berechnen oder mache ich da einen Denkfehler?
ich habe soeben selbst nochmals gerechnet und komme nun auf 14 Meter Durchmesser für die Milchstraße im besagten Beispiel. Unglaubliche Zahlen sind da im Spiel.
@Armin
14 m kommen hin. Überraschend groß im Verhältnis zur Größe des beobachtbaren Universums.
Ja das sind gewaltige Entfernungen wo man als kliner Mensch bei der Vorstellung dran verzweifelen kann.
Ich habe mal gelesen, das ein Raumfahrer es schaffen könnte in seiner Lebenbszeit, bei 99% von C unsere gesamte Milchstraße zu durchqueren. Dieses scheinbare Wunder kommt durch die Zeitdilatation zu Stande.
Wie weit käme dann ein Generationen Schiff, oder mit Hibernationskammern ausgerüstet, mit der gleichen Geschwindigkeit?
Jedoch bis zum äussersten heute sichtbaren Universum würde, keine noch so abstrackte Antriebsform ausreichen.
Werden die Menschen in der näheren Zukunft so weit ins All schauen, bis sie fast den Urknall erblicken.
@Commander1956
Der Grund, warum wir den Urknall nicht sehen können, ist nicht, dass er zu weit weg wäre. Die Hintergrundstrahlung ist gewissermaßen das Licht des Urknalls, wurde aber immer wieder von Materie im frühen Universum geschluckt und wieder abgestrahlt.
Die Strahlung ist durch diesen Prozess natürlich verändert worden, so wie die Strahlung, die wir von der Sonne erhalten, nicht direkt von der Temperatur der Fusion im Zentrum der Sonne abhängt, sondern von der der Sonnenoberfläche.
Wir können also auch in Zukunft nicht weiter blicken als wir es jetzt schon können – wir könnten aber unsere Messungen so verbessern, dass wir das Bild, das wir vom frühen Universum erhalten, genauer sehen können.
@Commander1956
Hmm, ich komme nur auf die ca. 7-fache Zeitdilatation bei 99% c (1/√(1-v²/c²) = 1/√(1-(0,99c)²/c²) = 1/√(1-0,99²), d.h. man käme in 100 Jahren Bordzeit gerade mal 693 Lichtjahre weit, das ist nicht mal ein Prozent des Durchmessers der Milchstraße. Das Problem ist, überhaupt solche Geschwindigkeiten zu erreichen, der Energieaufwand steigert sich ins Unermessliche, wenn es auf die Lichtgeschwindigkeit zu geht.
Rein technisch gesehen könnte man mit Generationenschiffen bei vielleicht 20% der Lichtgeschwindigkeit die nächsten Sterne erreichen, aber quer durch die Milchstraße ist mit lebender Besatzung technisch in absehbarer Zeit (und vermutlich für immer) nicht drin.
Netter Film zum Thema: Passengers aus 2016.
Bis fast zum Urknall „blicken“ wir schon seit 1964, als Penzias und Wilson die kosmische Hintergrundstrahlung mit ihrer Radioantenne entdeckten (das Licht des damaligen Feuerballs ist um das tausendfache durch die Expansion des Weltalls gedehnt worden und kommt als Radiostrahlung bei uns an). Das wird für immer unser Horizont für elektromagnetische Strahlung bleiben, und er entstand nur 380.000 Jahre nach dem Urknall. Nur mit Gravitationswellendetektoren oder Neutrinodetektoren kann man theoretisch noch ein näher an den Urknall heran.
Die fernsten bisher gesehenen Galaxien aus der Zeit, als die ersten Galaxien überhaupt entstanden, soll uns ab nächstem Jahr das James-Webb-Weltraumteleskop zeigen, das gerade im Ausdauertest in der Kältekammer ist. Hinter diesen ist bis zur Hintergrundstrahlung nicht mehr viel zu sehen, nur neutrales Gas.
Wenn man bis auf 1m/s an c herankommen würde, das wären ca. 99,9999997%, sollte es sich in ca. 8-9 Jahren Eigenzeit ausgehen wenn ich mich nicht verrechnet habe (was nicht unwahrscheinlich ist).
Und wenn jetzt noch irgendwie begreifbar erklärt werden könnte, warum die Lichtgeschwindigkeit die max. Geschwindigkeit darstellt. Also warum wird man nicht schneller wenn einen die Lichtgeschwindigkeit fortträgt und man zusätzlich in die selbe Richtung geht. Ist so eine Erklärung möglich, dass die auch ich begreife?
@Franz Xaver
Es gilt die Konstanz der Lichtgeschwindigkeit. Das ist die Grundlage der gesamten Relativitätstheorie: das Licht erscheint Dir immer gleich schnell. Wenn Du auf der Stelle hockst und mit einer Taschenlampe einen Lichtstrahl aussendest, entfernt er sich mit Lichtgeschwindigkeit von Dir. Wenn Du den Lichtstrahl bei Spazierengehen aussendest, entfernt er sich auch mit Lichtgeschwindigkeit von Dir. Aber auch mit derselben Geschwindigkeit von jemandem, der Dir auf der Stelle sitzend dabei zuschaut. Der Beobachter würde sagen, das Licht eilt Dir mit Lichtgeschwindigkeit minus Deine Schrittgeschwindigkeit voraus, aber Du würdest eine andere Geschwindigkeit messen, nämlich Lichtgeschwindigkeit.
Und das gilt immer noch, wenn Du mit 99% der Lichtgeschwindigkeit in Bezug auf den ruhenden Beobachter unterwegs bist. Der würde zwar messen, dass Dir das Licht nur mit 3000 km/s vorauseilt, aber aus Deiner Sicht wären es 300.000 km/s. Wie geht das?
Weil für Dich andere Maßstäbe und Zeiten gelten. Der ruhende Beobachter sähe Deine Zeit langsamer vergehen als Du. Dafür erschienen Dir zurückgelegte Strecken in der Welt des Beobachters verkürzt. Deswegen addieren sich Geschwindigkeiten nicht mehr so, wie wir das gewohnt sind. Es gilt das sogenannte relativistische Additionstheorem für Geschwindigkeiten. Das brauchst Du im Detail nicht nachzuvollziehen, aber es erklärt, warum Du noch so schnell unterwegs sein kannst, Du holst das Licht nie ein. Aus externer Sicht läuft Deine Zeit immer langsamer, die Masse Deiner Rakete nimmt auch noch zu, deswegen verbrennst Du den ganzen Treibstoff dafür, die Rakete immer schwerer zu machen, ohne dass sie viel schneller wird. Bei Lichtgeschwindigkeit wäre sie unendlich schwer, aber so weit kommt es letztlich nicht, das Licht bleibt immer einen Ticken schneller als Du und Dir erscheint es so, als ob Du ihm gar nichts an Geschwindigkeit abnehmen kannst.
Klingt alles sehr abgefahren, aber das ist genau das, was man messen kann: Licht ist immer gleich schnell, egal wie schnell man sich selbst bewegt. Der Rest folgt mit Mathematik. Und alles, was die Formeln vorhergesagt haben, wurde durch Beobachtungen bestätigt.
@Alderamin:
Ja, das Universum ist schon ein ziemlich verrückter Ort. Da sollte wirklich jeder hoffen, dass es eben gerade keinen Schöpfer gibt. Denn will man wirklich mit jemandem zu tun haben, der absichtlich ein derartiges Universum zusammenbaut?
@Franz Xaver, @Alderamin
„Klingt alles sehr abgefahren …“
Ja, das IST es auch – aus Sicht der Alltagserfahrung.
Ebenso wie die seltsamen Effekte, die in der „Quantenwelt“ auftreten.
Völlig meschugge …