Zeitdilatation oder Wie man 40-Minuten-Episoden in 20 Minuten schafft

Hinweis: Dieser Artikel ist ein Beitrag zum ScienceBlogs Blog-Schreibwettbewerb 2016. Hinweise zum Ablauf des Bewerbs und wie ihr dabei Abstimmen könnt findet ihr hier.

Das sagt die Autorin des Artikels, Ylva über sich:
Ich bin 16 und besuche die 12. Klasse eines Gymnasiums in Niedersachsen. Es ist das erste Mal, dass ich an einem solchen Wettbewerb teilnehme und einen Blogeintrag verfasse.

——————————————

Zeitdilatation oder Wie man 40-Minuten-Episoden in 20 Minuten schafft

Neulich habe ich mit einer Freundin die gesamte erste Staffel der amerikanischen Fernsehserie Veronica Mars geschaut. Aber vermutlich kennt jeder, der irgendwelche Serien schaut, den großen Nachteil daran: Man würde gerne immer noch mehr Episoden gucken, hat aber keine Zeit mehr, um alle zu schaffen. »Das ist halt das Problem, wenn man eine 40-Minuten-Episode in 20 Minuten schaffen will«, brachte meine Freundin es ziemlich genau auf den Punkt. Ich stimmte ihr zu, überlegte aber: Warum sollte das eigentlich nicht gehen?

Aufgrund des G8 sowie den neu angepassten und entrümpelten Lehrplänen wurde die Spezielle Relativitätstheorie leider aus dem Kerncurriculum für die gymnasiale Oberstufe in Niedersachsen gestrichen. Aber auch wenn wir in der Schule nichts mehr darüber lernen, kann man sich ja trotzdem einmal damit beschäftigen. Immerhin liefert sie die Lösung für unser Problem.

Die Spezielle Relativitätstheorie wird von vielen Leuten als kompliziert angesehen, was höchstwahrscheinlich daran liegt, dass sie unser intuitives Konzept von Raum und Zeit auf den Kopf stellt. Allerdings basiert sie auf nur zwei Postulaten (das sind wissenschaftliche Festlegungen, die dann immer gültig sind), und wenn man diese erst einmal verstanden hat, hat man schon ziemlich viel gewonnen. Das erste Postulat besagt einfach, dass die Lichtgeschwindigkeit immer konstant ist (und zwar bei etwa 300.000 km/s). Das klingt auf den ersten Blick ziemlich simpel, allerdings widerspricht schon das unserem normalen Verständnis von Geschwindigkeit. Wenn man neben einem vorbeifahrenden ICE steht, würde man dessen Geschwindigkeit mit 200km/h messen. Wenn man jedoch mit einem 150km/h schnellen Auto nebenher fährt, würde man nur noch 50km/h für den ICE messen. Wenn man eine andere Geschwindigkeit misst, ist es also wichtig, wie schnell man selbst ist. Beim Licht ist das aber egal. Es macht keinen Unterschied, wie schnell man sich selbst bewegt, die Lichtgeschwindigkeit wird immer mit 300.000km/s bemessen. Klingt seltsam, ist aber schon erfolgreich im Michelson-Morley-Experiment nachgewiesen worden.

Und schon geht es weiter zum zweiten Postulat: dem Relativitätsprinzip. Bewegung gibt es nur relativ zu etwas anderem. Wenn man zum Beispiel in dem ICE von eben säße, ohne aus dem Fenster schauen zu können, könnte man nicht feststellen, dass man sich bewegt (vorausgesetzt natürlich, dass der ICE mit konstanter Geschwindigkeit geradeaus fährt und die Schienen nicht zu marode sind). Schließlich kann man sich dort genau so bewegen wie auf der Erde und es gelten die gleichen physikalischen Gesetze. Schaut man nun aus dem Fenster, sieht man, dass die Erde sich bewegt, während man selbst in Ruhe ist. Die Erde ist für den Zugfahrer also relativ (d.h. in Bezug auf) zum ICE bewegt.

Ein Beobachter am Bahnhof würde hingegen sagen, dass die Erde in Ruhe ist und der Zug relativ zur Erde bewegt ist. Wer hat nun Recht? Nach der Speziellen Relativitätstheorie kann man sich aussuchen, was ruht und was bewegt ist, solange man zwei Systeme hat, die relativ zueinander bewegt sind. Eine Einschränkung gibt es allerdings: Bremst der Zug zum Beispiel abrupt, gelten dort andere physikalische Gesetze als in einem ruhenden System. Gegenstände fallen nicht mehr nach unten, sondern fliegen nach vorne. Jetzt ist der Zug zwangsläufig das »bewegte« System und kann nicht mehr als ruhend angesehen werden. Das ist später nochmal wichtig.

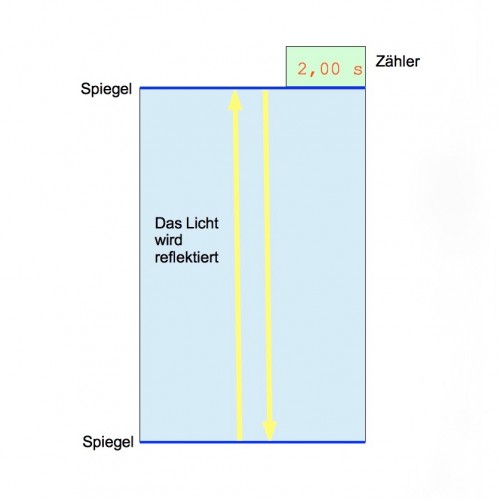
Ausgerüstet mit diesen Postulaten, kann man sich jetzt einer sehr schönen Aussage der Speziellen Relativitätstheorie widmen: Bewegte Uhren gehen langsamer. Erklären kann man das am besten mit einer Lichtuhr. Diese besteht aus zwei Spiegeln, zwischen denen ein Lichtsignal immer reflektiert wird und immer wenn das Licht einen Spiegel passiert, wird eine Zeiteinheit gemessen.

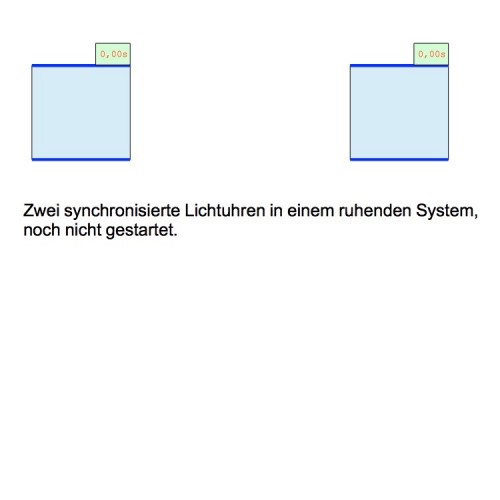
Hätte man eine 300.000km hohe Lichtuhr, würde man zum Beispiel immer eine Sekunde messen. (Anmerkung: Lichtuhren sind ein theoretisches Konstrukt von Albert Einstein, das heißt, es gibt sie nicht wirklich.) Wir brauchen jetzt zwei Lichtuhren in einem ruhenden System. Diese beiden sind synchronisiert, das heißt, sie laufen gleich.

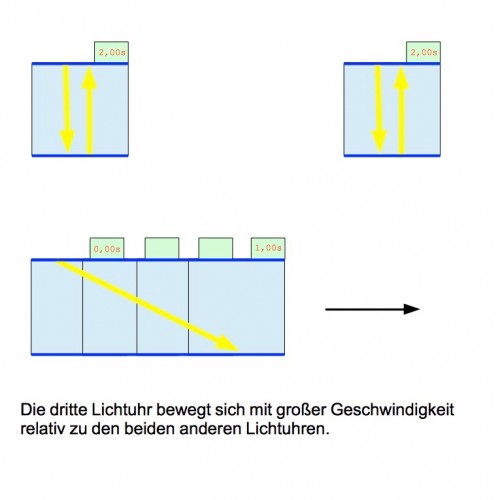
Jetzt kommt eine dritte Lichtuhr, die mit großer Geschwindigkeit an den beiden anderen Uhren vorbeiläuft. Passiert sie die erste Uhr, werden alle Lichtuhren gestartet, passiert sie die zweite Uhr, werden alle drei gestoppt.

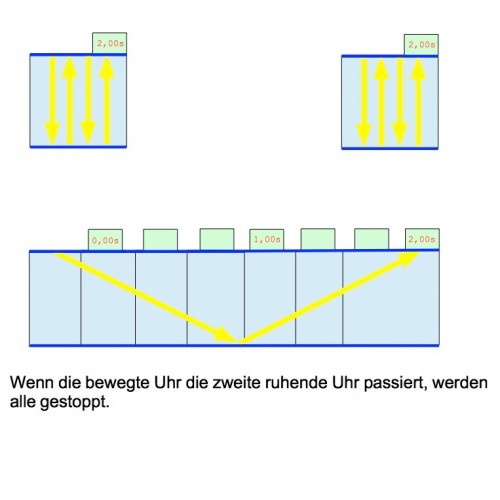
Was zeigen die Uhren jetzt an? In den beiden ruhenden Uhren wurde das Licht insgesamt viermal reflektiert. In der bewegten Uhr musste das Licht einen längeren Weg von einem Spiegel zum anderen zurücklegen, da das Licht jetzt nicht mehr gerade nach unten läuft, sondern einen diagonalen Weg nimmt. Um viermal reflektiert zu werden, hätte das Licht also eine größere Strecke (Die Diagonalen sind logischerweise länger als der gerade Weg von einem Spiegel zum anderen) in der gleichen Zeit wie das Licht in den ruhenden Uhren zurücklegen müssen. Das Licht in der bewegten Uhr hätte also schneller als das Licht in den anderen Lichtuhren sein müssen. Das geht aber laut dem ersten Postulat nicht. Daher kann das Licht nur zweimal reflektiert werden, weil es aufgrund der konstanten Lichtgeschwindigkeit nur zwei Diagonalen statt vier schafft. Hätten wir jetzt 300.000km hohe Lichtuhren, würden die ersten beiden Uhren 4 Sekunden, die dritte Uhr aber nur 2 Sekunden anzeigen. Die bewegte Uhr geht also tatsächlich langsamer; dieses Phänomen wird Zeitdilatation (von lat. dilare = dehnen) genannt. Dies gilt nicht nur für theoretische Lichtuhren, sondern für alle möglichen realen Uhren, mit den Lichtuhren kann man es nur besser erklären. Natürlich kann man auch ausrechnen, wie viel langsamer die Uhr bei einer bestimmten Geschwindigkeit ist (Wen es interessiert: Einfach mal die Herleitung für die Zeitdilatation in einer Formelsammlung nachschlagen). Die Zeitdilatation tritt auch in unserem alltäglichen Leben auf, wir bekommen nur nichts davon mit, weil man sich sehr schnell bewegen muss, damit sie überhaupt messbar wird. Und sehr schnell heißt in diesem Fall mit einem signifikanten Anteil der Lichtgeschwindigkeit, also eher mit 1.000.000km/h statt mit 100km/h.

Um zurück auf das ursprüngliche Problem zu kommen: Wenn wir 40 Minuten in 20 Minuten schaffen wollen, müssten für mich und meine Freundin 40 Minuten vergehen, während für alle anderen nur 20 Minuten vergehen. Könnten wir also einfach in ein Raumschiff steigen, dass mit 87% der Lichtgeschwindigkeit 20 Minuten von der Erde wegfliegt und dann wieder in 20 Minuten zurückkommt? (Wer sich wundert, wie ich auf 87% komme: Die Rechnung habe ich am Ende einmal aufgeschrieben, da Formeln mitten im Text eher abschreckend wirken.) Für uns sähe es dann ja so aus, als wären wir in Ruhe, während sich die Erde schnell von uns wegbewegt und dann wieder schnell zu uns hinbewegt. Die Zeit müsste dort also nur halb so schnell vergehen, das heißt, für uns 40 Minuten, für alle anderen 20. Dabei übersehen wir aber eine sehr wichtige Sache: Um zu starten, zu wenden und wieder abzubremsen, muss das Raumschiff beschleunigt werden. Und damit können wir unser System nicht mehr als ruhend ansehen. (Das ist das Gleiche wie mit dem abbremsenden ICE aus dem ersten Beispiel.) Wir sind also im bewegten System und für uns vergeht die Zeit nur halb so schnell, während sie für alle anderen normal schnell vergeht. Messen wir 40 Minuten, vergehen für alle anderen 80 Minuten! Das ist so ziemlich das Gegenteil von der Lösung für unser Problem.

Was heißt das? Wir müssten ziemliche Überzeugungsarbeit leisten, um die gesamte Weltbevölkerung auf ein Raumschiff zu schicken, das für 10 Minuten von der Erde wegfliegt und dann zurückkommt. Dabei wäre die Überzeugung wohl noch das kleinere Übel, denn heutzutage schaffen die Raumschiffe noch nicht mal 1% der Lichtgeschwindigkeit und selbst auf den größten von ihnen ist nur Platz für wenige Leute. Aber das sind eigentlich nur noch technische Probleme, keine grundsätzlichen. Und wer weiß, in ferner Zukunft könnten wir vielleicht tatsächlich einmal in 20 Minuten eine 40-Minuten-Veronica-Mars-Episode schaffen. Man erkennt also: Blieben die Überlegungen der Speziellen Relativitätstheorie nicht nur theoretisch, wären sie ganz schön praktisch.

(Anmerkung: In diesem Eintrag habe ich mich nur auf die Zeitdilatation bezogen, die von der Speziellen Relativitätstheorie vorhergesagt wird. Eigentlich müsste auch die gravitative Zeitdilatation berücksichtigt werden, die sich aus der Allgemeinen Relativitätstheorie ergibt. Das würde das Ganze aber etwas komplizierter machen.)