Will Hunting und die Graphentheorie

Dieser Gastartikel ist ein Beitrag zum ScienceBlogs Blog-Schreibwettbewerb. Alle eingereichten Beiträge werden im Lauf des Septembers hier im Blog vorgestellt. Danach werden sie von einer Jury bewertet. Aber auch alle Leserinnen und Leser können mitmachen. Wie ihr eure Wertung abgeben könnt, erfahrt ihr hier.

Dieser Beitrag wurde von Lukas Prader eingereicht.
———————————————————————————————————————–
Will Hunting und die Graphentheorie

Ich schalte den Fernseher an, öffne den Teletext – und da lese ich es! Robin Williams ist tot. Kaum zu glauben! Unendlich schade um diesen brillanten Schauspieler mit seinen abwechslungsreichen Rollen.
Offenbar versuchten auch die Fernsehsender, den Tod des Stars aufzuarbeiten. Kurzerhand disponierten sie ihre Abendprogramme um – und so wurde bestimmt jeden Tag irgendwo ein Robin-Williams-Film gezeigt.

Als (angehender) Mathematiker hat mich natürlich einer davon ganz besonders interessiert: Good Will Hunting. Williams verkörpert darin die Rolle des Psychologen Sean Maguire, für die er mit einem Oskar ausgezeichnet wurde. Im Film geht es aber vor allem um das Aufeinandertreffen zweier scheinbar gegensätzlicher Menschen: Auf der einen Seite der Hausmeister Will Hunting, auf der anderen der MIT-Professor Gerald Lambeau, der gar ein Empfänger der überaus renommierten Fields-Medaille (quasi des „Mathematik-Nobelpreises“) ist. Lambeau interessiert sich sehr für Will – warum, mögen Sie fragen. Wie kann ein Hausmeister einen Mathematiker begeistern? Ganz einfach: Mit Mathematik! Will entpuppt sich als wahres Mathematikgenie und letztlich muss Lambeau sogar gestehen, dass er Will in seinem eigenen Fach eindeutig unterlegen ist. Wahrscheinlich halten das viele Leute für Fiktion, was es allerdings nicht ist! Mathematische Wunderkinder (oder eben Wundererwachsene wie Will), die aus dem Nichts auftauchen und mit den „echten“ Mathematikern konkurrieren, sind zwar nicht häufig, aber es gibt sie tatsächlich. Der indische Buchhalter Srinivasa Ramanujan, der mit seinen Briefen die britische Mathematikelite begeisterte, ist das wohl bekannteste Beispiel für einen Will Hunting des wahren Lebens.

Auch im Film ist es so, dass Professor Lambeau eher durch Zufall auf Wills Talent aufmerksam wird: Er erwischt ihn dabei, wie er ein Rätsel auf einer Gangtafel (völlig korrekt) löst, das für seine Studenten bestimmt war. Zwei Jahre lang hätten die MIT-Professoren für die Lösung gebraucht, gesteht er in einer Vorlesung. Dementsprechend entsetzt ist er natürlich, als er erkennt, wie mühelos Will damit fertig wird. Tatsächlich handelt es sich dabei aber um ein Rätsel, das jeder von uns verstehen und lösen kann – und das werden wir im Laufe dieses Textes auch tun! Zugegeben: Die Aufgabenstellung ist das einzig Komplizierte am ganzen Rätsel. Die Lösung ist weitaus leichter. Versprochen! Ich haue die Angabe jetzt ganz einfach raus – danach gehen wir sie Wort für Wort durch und lösen das Rätsel. Also nicht schrecken! Abgemacht? – Na dann:

„Finden Sie alle nicht-isomorphen, homöomorph irreduziblen Bäume vom Grad zehn.“

Ich nehme an, Sie haben bereits alles verstanden. Dann können wir ja fortfahren … Haha, jetzt habe ich mir mit Ihnen einen Spaß erlaubt – wird nicht wieder vorkommen. Als ich das zum ersten Mal gelesen habe, habe ich auch nur Bahnhof verstanden. Das Rätsel wird uns tief in die Graphentheorie führen – eine mathematische Teildisziplin, die sich mit ganz speziellen Strukturen befasst. Um herauszufinden, was genau ein solcher Graph ist und wofür man sie braucht, unternehmen wir eine kleine Zeitreise ins 18. Jahrhundert:

Das preußische Königsberg … Eine Stadt mit einer langen Geschichte. Der Fluss Pregel durchzieht das Stadtzentrum. Erst zweigeteilt vereinigen sich hier die Flussarme, schließen eine Insel ein (den Kneiphof) und vereinigen sich anschließend wieder. Reihenhäuser zieren die Ufer, auf dem Wasser tummeln sich Schiffe und zahlreiche Enten. Ein großer Dom auf dem Kneiphof überragt die Reihenhäuser. Um alle Stadtteile bequem erreichen zu können, wurden sieben Brücken errichtet (siehe dazu die Karte unten). Sie sind er Gegenstand einer Frage, die die Bewohner er Stadt seit jeher quält, aber nach wie vor unbeantwortet ist: Kann man auf einen Stadtspaziergang jede der sieben Brücken genau einmal überqueren? Genau einmal – das bedeutet, man darf weder eine Brücke auslassen noch zweimal oder gar öfter über sie flanieren. Wie kann man so eine Frage überhaupt angehen? Die Königsberger spazieren und spazieren, sitzen vor ihren Landkarten … Es gelingt ihnen einfach nicht, eine Route zu finden.

Zurück in die Gegenwart: Um die Lösungssuche voranzutreiben, wandte sich der damalige Bürgermeister der Stadt Danzig an den Schweizer Mathematiker Leonard Euler. Bald erkannte dieser, dass das Stadtzentrum vom Fluss in vier Teile zerschnitten wird. So bezeichnete er auf einer Skizze jeden Stadtteil mit einem Buchstaben und zeichnete die Brücken als Striche zwischen den einzelnen Buchstaben ein. Was er erhielt, gilt als der allererste Graph – und damit war das die Geburtsstunde der Graphentheorie.

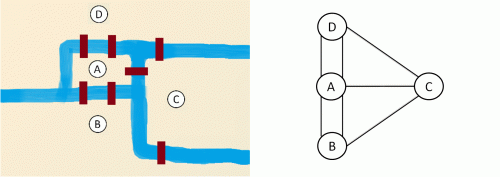
Ein Graph – das sind Punkte (in unserem Fall die Stadtteile), die durch Striche (Brücken) miteinander verbunden sind. Alle Punkte eines Graphen müssen irgendwie zusammenhängen – das ist eine Regel. Es darf quasi keine Stadtteile geben, die für die Fußgänger unerreichbar sind. Das macht auch Sinn; außer man baut extra einen Hafen, um eine Brücke zu vermeiden … Eine zweite Regel besagt, dass sich zwei Striche nicht kreuzen dürfen – außer natürlich in einem Punkt. Wenn sich also zwei Striche treffen, muss dort demnach auf jeden Fall ein Punkt sein.

Mit seinem Graphen konnte Euler in einer Arbeit aus dem Jahre 1736 erklären, warum alle Bemühungen der Königsberger vergeblich waren und auch vergeblich bleiben würden: Einen solchen Spaziergang konnte es gar nicht geben! Natürlich behauptete er das nicht, ohne es rigoros zu untermauern: Ein Spaziergang wäre genau dann möglich, schrieb er, wenn höchstens zwei Punkte mit einer ungeraden Zahl von Strichen verknüpft wären (die restlichen mit einer geraden Zahl von Strichen). In Königsberg ist das jedoch nicht der Fall, da kein einziger der Stadtteile A, B, C oder D mit einer geraden Anzahl an Brücken verbunden ist. Wer sich gerne noch weiterhin mit dem „Königsberger Brückenproblem“ beschäftigen möchte, könnte eine Karte des heutigen Königsbergs betrachten: Zwei Brücken des Stadtzentrums wurden im Zweiten Weltkrieg zerstört. Ist dadurch vielleicht ein Spaziergang möglich geworden?

Jetzt aber zurück zum Rätsel: Es geht also darum, ganz spezielle Bäume zu zeichnen. Natürlich keine Buchen, Tannen oder Flaumeichen, sondern „mathematische“ Bäume. Das sind Graphen, in denen es keine Kreise gibt. Was bedeutet das? – Sehen wir uns noch einmal Eulers Graph an: Wir können vom Punkt A zu Punkt C spazieren, von Punkt C zu Punkt B, und kommen (über einen der beiden Striche) von B nach A zurück. Wir sind also zu unserem Startpunkt zurückgekehrt, ohne irgendwo „rückwärts gehen“ zu müssen. Wenn man das kann, muss es offensichtlich einen Kreis im Graphen geben. Eulers Graph ist folglich kein Baum, sehr wohl aber die drei Graphen in diesem Bild:

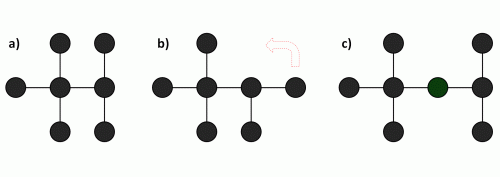
Die Bäume in unserem Rätsel sollen zudem vom Grad 10 sein. Das bedeutet, dass die Bäume aus genau 10 Punkten bestehen müssen – nicht aus mehr und nicht aus weniger. Ein Beispiel: Baum a und Baum b sind vom Grad 7, Baum c vom Grad 8.
Außerdem sollen die Bäume homöomorph irreduzibel sein. In unserem Fall bedeutet das ganz einfach, dass ein Punkt nicht mit genau zwei anderen Punkten verbunden sein darf. Warum das eine sinnvolle Einschränkung ist, sehen wir an Baum c: Achten wir auf den grünen Punkt! Im Grunde ist er ja vollkommen unnötig. Man müsste den Strich dort nicht unterbrechen, da ihn weder ein anderer Strich kreuzt noch ein Strich von ihm abzweigt. Um diesen Baum homöomorph irreduzibel zu machen, muss also der grüne Punkt entfernt werden (was uns geradewegs zu Baum a führt). Mit dieser Regelung bekommt man auch das „Punkte-Schinden“ in den Griff. Denn dort, wo der grüne Punkt ist, könnte man im Prinzip so viele Punkte zeichnen, wie man möchte – ob das jetzt zwei sind, oder 10, oder 100, wäre ganz dem Zeichner überlassen.

Da fällt mir ein: Mathematische Bäume haben tatsächlich eine Gemeinsamkeit mit den Bäumen in der Natur. – Nein, es gibt keine Nationalparks, in denen wir sie nicht anrühren dürfen. (Wäre auch sinnlos: Wenn wir einen mathematischen Baum „fällen“, könnten wir ihn mit Zettel und Stift wieder zum Leben erwecken.) Die Gemeinsamkeit ist, dass mathematische Bäume auch Blätter tragen. So werden Punkte genannt, die mit nur einem anderen Punkt verbunden sind.
Zum Abschluss muss noch geklärt werden, was nicht-isomorph heißt. Am besten kann man das anhand von Baum a und Baum b erklären: Wenn ich das äußerst rechte Blatt von Baum b in Pfeilrichtung verbiege, sieht Baum b exakt gleich aus wie Baum a (man sagt: sie haben dieselbe Struktur). Dabei wird deutlich: Man kann aus einem Baum viele unterschiedliche Bäume erzeugen, indem man etwa einzelne Striche streckt oder verdreht, den ganzen Baum spiegelt oder kippt, etc. Alle Bäume, die auf diese Weise entstehen können, nennt man isomorph. Weil im Rätsel aber ausdrücklich nicht-isomorphe Bäume gefordert werden, bedeutet das, dass immer nur ein Baum (stellvertretend für all seine isomorphen Kollegen) gezählt wird. Baum a und Baum b würden im Rätsel quasi auch nur als ein einziger Baum gelten.

Bevor wir gleich loslegen, noch einmal die Regeln im Überblick:
– Der Graph darf keine Kreise enthalten.
– Es müssen 10 Punkte verwendet werden.
– Ein Punkt darf nicht mit genau zwei anderen Punkten verbunden sein.
– Zwei Bäume dürfen nicht isomorph sein.

Eine Frage bleibt uns aber noch: Wie gehen wir die Suche am geschicktesten an? Wenn wir uns in diesem förmlichen Wald von Bäumen zurechtfinden wollen, brauchen wir auf jeden Fall eine zuverlässige Landkarte, die uns zum Ziel führt. Ich habe mir dazu Folgendes überlegt:
Als erstes werden wir immer eine Kette bilden. Erst besteht sie nur aus einem Punkt (ist dann eigentlich keine Kette, aber egal), dann aus zwei Punkten, dann aus dreien, und immer so weiter. Sie wird quasi der „Stamm“ unseres Baumes sein. Die restlichen Punkte verteilen wir dann als Blätter auf jene Stammpunkte.
Beginnen wir mit dem einfachsten Baum: Wie sieht der aus? – Ganz einfach: Ein Punkt kommt in die Mitte (die berüchtigte Ein-Punkt-Kette), die verbleibenden neun hängen wir als Blätter an. So haben wir schon unseren ersten Baum, beziehungsweise unsere erste Schneeflocke (zumindest erinnert mich dieser Baum immer an eine).

Als nächstes ist der Stamm eine Zweierkette, die restlichen acht Punkte werden wieder verteilt. Eine kurze Zwischenfrage: Wie viele Blätter müssen wir jedem dieser Punkte mindestens zuordnen? – Zwei! Eines alleine würde nicht reichen – dann wäre der Punkt nämlich mit genau zwei anderen Punkten verbunden (dem Blatt und dem anderen Punkt). Das ist aber verboten! Welche Möglichkeiten haben wir also zur Verteilung der Blätter? – 6 und 2 … 5 und 3 … 4 und 4. Jetzt aber Achtung: „3 und 5“ ist dasselbe wie „5 und 3“, nur ist der Baum (um 180°) verdreht. Deswegen zählen sie nur als ein Baum – das Gleiche gilt auch für „2 und 6“ und „6 und 2“. Das führt uns zu unseren ersten vier Bäumen. Spoiler-Alarm: Gleich ist Halbzeit.

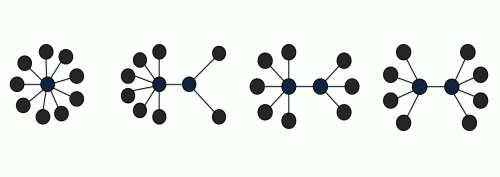
Wie geht es jetzt weiter? – Genau: Eine Dreierkette als Stamm, sieben Blätter müssen verteilt werden. Aber bevor wir uns die Mühe machen und alle möglichen Kombinationen einzeln durchgehen (4 und 1 und 2 … 3 und 2 und 2 … etc.), wenden wir einen kleinen Trick an: Dem mittlere Stammpunkt geben wir seine Blätter zuerst. Wir beginnen mit einem Blatt, dann bekommt er zwei, dann drei, und so weiter. Dass Außenpunkte mindestens zwei Blätter brauchen, haben wir vorher schon erkannt. Wie sieht es mit dem mittleren Punkt aus? – Na ja, eines braucht er unbedingt, ansonsten würde er gegen die 2-Verbindungen-Regel verstoßen (die benachbarten Stammpunkte). Weil dieses eine Blatt aber schon reichen würde, können wir folgern: Er braucht mindestens ein Blatt. Das bekommt er – es bleiben sechs Blätter für die äußeren Stammpunkte. Mögliche Aufteilungen: 4 (und 1) und 2 … 3 (und 1) und 3. Nun geben wir dem mittleren Stammpunkt zwei Blätter. Wie verteilen wir die restlichen? – 3 (und 2) und 2. Mehr Möglichkeiten haben wir gar nicht. Als nächstes drei Blätter in die Mitte. – Wieder gibt es nur eine Möglichkeit: 2 (und 3) und 2.

Können wir vier Blätter in die Mitte geben? Dann würden immerhin noch drei Blätter für die Außenpunkte übrig bleiben. Aber wir wissen, dass jeder Außenpunkt zwei Blätter benötigt – mindestens! Das geht sich nicht aus – wir können also nicht mehr drei Blätter an den mittleren Stammpunkt hängen.

Würden wir jetzt fortfahren, dann würde uns ein Baum mit Dreierkette entgehen! Wie kann das denn sein? Sehen wir uns noch einmal den vorigen Baum (Verteilung 2 und 3 und 2) an: Die 3 Punkte am mittleren Stammpunkt verwenden wir allesamt als Blätter. Es spräche aber nichts dagegen, nur einen der Punkte direkt an den Stammpunkt anzuschließen (im Bild unten habe ich ihn grau dargestellt) und ihm dann die zwei bleibenden Blätter anzuhängen. Auf diese Weise erhalten wir schließlich unseren neunten (zugegeben recht schwierig zu findenden) Baum.

Keine Frage, wie es jetzt weitergeht: Eine Viererkette bildet den Stamm, daher gibt es diesmal zwei äußere und zwei innere Stammpunkte. Da jeder äußere Stammpunkt mindestens zwei Blätter benötigt und jeder innere mindestens einen, geht es sich exakt aus mit unseren sechs Blättern. Es gibt also nur eine Möglichkeit – (2 und 1 und 1 und 2) – und die ist nicht wirklich verzwickt zu finden. Damit sind es schon 10 Bäume:

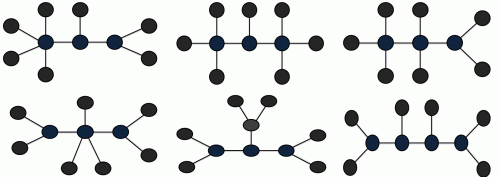
Was passiert, wenn unsere Stammkette aus noch mehr als nur vier Punkten besteht? Probieren wir es einfach einmal mit fünf aus: In dem Fall gibt es zwei äußere und drei innere Stammpunkte, was bedeutet: Wir benötigen sieben Blätter. Die haben wir aber nicht – uns bleiben ja nur mehr fünf Stück übrig. Mit noch längeren Stammketten brauchen wir es dann gar nicht erst versuchen: Es bleibt also bei unseren 10 nicht-isomorphen, homöomorph irreduziblen Bäumen vom Grad 10. (Anmerkung: Es ist Zufall, dass es genau 10 Bäume vom Grad 10 gibt. Es existieren beispielsweise 5 solche Bäume vom Grad 9 und 14 Bäume vom Grad 11.)

Bleiben wir aber realistisch: Echte MIT-Professoren hätten dieses Rätsel mit Sicherheit noch schneller gelöst als wir gerade eben. Daniel Kleitman, der mathematische Berater des Films, hat sich da offensichtlich einen Spaß mit seinem Publikum erlaubt. Die Figuren, die Will an die Tafel kritzelt, wirken eindrucksvoll und komplex und lassen das Publikum darum an den teuflischen Schwierigkeitsgrad der Aufgabe glauben.

Uns wird also ein leichtes Rätsel als äußerst schwer verkauft. Aber mal ehrlich: Es war die einzige Möglichkeit! Wie viele mathematische Rätsel gibt es denn, an denen MIT-Professoren zwei Jahre lang zu knabbern hätten, die sich aber recht anschaulich auf einer Gangtafel lösen lassen? Wenn es überhaupt solche Rätsel gibt – ich bezweifle es – dann sind sie unglaublich schwer zu finden.

Jedenfalls ist es ein hochinteressantes Thema, das uns „Good Will Hunting“ näherbringt. Einerseits haben wir so die Graphentheorie kennengelernt – ein Teilgebiet der Mathematik, dem wir jeden Tag begegnen, auch wenn wir es nicht unbedingt merken: Jede Straßenkarte, jeder U-Bahn-Plan basiert auf den Ideen, die Leonard Euler schon vor rund 300 Jahren hatte. Und andererseits haben wir dieses Rätsel gelöst – ein Rätsel für Jedermann und für überall, wo man Zettel und Stift zur Hand hat. Einem Phänomen, das in der Mathematik generell häufig ist, begegnet man auch hier: Nur weil etwas wahnsinnig kompliziert klingt, heißt das nicht, dass es sich nicht doch als einfach herausstellen kann.

Wen jetzt jedenfalls die Begeisterung übermannt hat, kann die nächsten Hürden auf sich nehmen: Grad 11, Grad 12, etc. Wer aber die infernale Herausforderung sucht, kann sich dem Grad 3 widmen. Warum? – Sehen Sie selbst!