 Das ist die Transkription einer Folge meines Sternengeschichten-Podcasts. Die Folge gibt es auch als MP3-Download und YouTube-Video. Und den ganzen Podcast findet ihr auch bei Spotify.
Das ist die Transkription einer Folge meines Sternengeschichten-Podcasts. Die Folge gibt es auch als MP3-Download und YouTube-Video. Und den ganzen Podcast findet ihr auch bei Spotify.
Mehr Informationen: [Podcast-Feed][iTunes][Bitlove][Facebook] [Twitter]
Über Bewertungen und Kommentare freue ich mich auf allen Kanälen.
—————————————————
Sternengeschichten Folge 446: Das Konzil der Riesen
Heute geht es um das „Konzil der Riesen“. Das klingt ein bisschen wie aus einem Fantasy-Roman. Hat aber gar nichts damit zu tun, sondern mit Kosmologie. Und Galaxien. Dazu reisen wir in die „Lokale Gruppe“. Das klingt ein wenig langweilig; ist aber die offizielle Bezeichnung für unsere Ecke im Universum. Also die Ansammlung von Galaxien, zu der auch die Milchstraße gehört; unsere Heimatgalaxie in der sich die Sonne befindet. Die lokale Gruppe habe ich in Folge 371 schon einmal ausführlich vorgestellt; das werde ich jetzt nicht wiederholen. Die Kurzversion: Die Lokale Gruppe besteht aus den beiden großen Galaxien der Milchstraße und der Andromeda. Dazu kommen noch ein paar Dutzend kleinere Galaxien, die alle durch ihre Gravitationskraft aneinander gebunden sind. Das heißt, dass sie sich nicht unabhängig voneinander durch den Weltraum bewegen können, sondern einander mit ihrer Gravitationskraft in Form eines Galaxienhaufens zusammenhalten. Dieser Haufen hat einen Durchmesser von circa 8 Millionen Lichtjahren. Aber hinter der lokalen Gruppe hört das Universum natürlich nicht auf. Es gibt unzählige andere Galaxienhaufen, die sich zu noch größeren Superhaufen zusammenfinden, die wiederum Super-Superhaufen bilden, und so weiter. Und zwischen diesen gigantischen Strukturen gibt es ebenso gigantische Leerräume.
Schaut man ein wenig über die lokale Gruppe hinaus, findet man also weitere Galaxien. Die nicht willkürlich angeordnet sind. Die Galaxien in unserer Umgebung bilden zusammen mit der lokalen Gruppe die sogenannte „Lokale Scheibe“. Der offizielle englische Fachausdruck dafür lautet „local sheet“ und es handelt sich tatsächlich um eine Region, die ungefähr 50 Millionen Lichtjahre durchmisst und nur 1,5 Millionen Lichtjahre dick ist. Eine Scheibe, voll mit Galaxien, die alle mehr oder weniger die gleiche „Pekuliargeschwindigkeit“ haben. Das Wort „pekuliar“ bedeutet so viel „eigentümlich“; so eigentümlich ist die Sache aber gar nicht. Man meint damit in der Astronomie einfach nur die Geschwindigkeit eines Objekts in Bezug auf etwas anderes. In diesem Fall ist die Sache ein wenig knifflig, weil es um Kosmologie geht. Seit über hundert Jahren wissen wir, dass das Universum sich ausdehnt. Edwin Hubble und seine Kollegen haben in den 1920er Jahren gemessen, dass sich alle Galaxien voneinander entfernen und zwar um so schneller, je weiter sie voneinander entfernt sind. Man muss aber aufpassen, wie man diese Aussage interpretiert. Das gilt so allgemein nur, wenn man das Universum wirklich auf sehr großen Skalen betrachtet. Die Erde selbst etwa, hat immer die gleiche Größe, die dehnt sich nicht aus. Auch die Abstände der Planeten des Sonnensystems zur Sonne bleiben gleich. Und vorhin habe ich gesagt, dass die Galaxien der lokalen Gruppe durch ihre Gravitationskraft aneinander gebunden sind; hier sorgt die Expansion des Universums also auch nicht dafür, dass sich alle voneinander entfernen. Man kann sich die Expansion als eine Kraft vorstellen und die Gravitation als andere Kraft. Bei – kosmologisch gesehen – kleinen Abständen, ist die Gravitationskraft stärker als die Expansion und hält die Dinge zusammen. Deswegen bleibt der Abstand der Planeten zur Sonne gleich und auch die lokale Gruppe löst sich nicht auf. Nur wenn es um sehr weit voneinander entfernte Objekte geht, spielt die Expansion des Alls eine Rolle.

Man darf die Bewegung der Galaxien aufgrund der Expansion des Raums auch nicht mit einer Bewegung DURCH den Raum verwechseln. Vereinfacht gesagt wird der Raum zwischen den Galaxien immer größer und die Galaxien werden dadurch voneinander weg „geschoben“. Wir sehen trotzdem, wie sie sich – gemeinsam mit dem Raum – von uns entfernen und können die entsprechende Geschwindigkeit messen, mit der sie das tun. Das ist aber nicht die Pekuliargeschwindigkeit, um die es geht. Das ist tatsächlich die Geschwindigkeit, mit der sich eine Galaxie DURCH den Raum bewegt. Und bestimmt man die für die großen Galaxien in unserer Umgebung, dann sieht man, dass die alle recht gut übereinstimmen. Und sich von der Pekuliargeschwindigkeit der weiter entfernten Galaxien unterscheidet. Genau das ist die lokale Scheibe: Eine große Gruppe an Galaxien, die sich alle mit ungefähr der gleichen Geschwindigkeit in die gleiche Richtung bewegen. Wer wissen möchte, wohin die Reise geht: Zum sogenannten „Leo Spur“. Das ist eine andere „lokale Scheibe“, also eine andere Ansammlung von Galaxien die sich Bewegungsrichtung und Geschwindigkeit teilen. Bis wir dort ankommen, werden aber noch circa 10 Milliarden Jahre vergehen; wir können uns als noch entspanden.
Der Grund der gemeinsamen Bewegung der Galaxien in der lokalen Scheibe ist eine weitere Lokalität: Nämlich die „Lokale Leere“. Ich habe vorhin schon von der großräumigen Struktur des Universums gesprochen: Riesige Superhaufen aus Galaxien, getrennt von ebenso riesigen Leerräumen. Die aus den Galaxien-Superhaufen gebildeten Strukturen werden offiziell „Filamente“ genannt, die Leerräume heißen „Voids“. Die lokale Scheibe ist, auf einem etwas kleinerem Maßstab, genau so ein Filament, ebenso der Leo Spur (der das uns nächstgelegen Filament ist). Und direkt an die lokale Scheibe grenzt eine Void. Wir wissen nicht, wie groß dieser Leerraum genau ist, aber so um die 50 Millionen Lichtjahre im Durchmesser wird das Nichts schon groß sein. Und diese lokale Leere schiebt uns in Richtung Leo Spur. Ok, das ist physikalisch nicht ganz sauber. Ein Leerraum kann nicht „schieben“; der macht gar nichts; der ist einfach nur da und leer. Aber wenn überall um uns herum andere Galaxien sind, nur in einer Richtung – nämlich da wo der Leerraum ist – nicht, dann wirken die entsprechenden Gravitationskräfte genau so zusammen, dass es aussieht, als würde der Leerraum uns von sich wegschieben.
Fassen wir einmal kurz zusammen; mit dem ganzen lokalen Dies und lokalen Das wird es ja schnell verwirrend. Wir leben in der Milchstraßengalaxie. Zusammen mit einem Schwung anderer Galaxie bildet sie eine Galaxiengruppe, die „Lokale Gruppe“ genannt wird. Die Lokale Gruppe wiederum bildet mit noch mehr anderen Galaxien die lokale Scheibe, ein Filament, das quasi eine Wand bildet, die an die lokale Leere grenzt, einen enorm großen Teil des Universums in dem sich so gut wie gar nichts befindet. So etwas ist gut zu wissen; man sollte immer darüber informiert sein, wo man in der Welt und im Universum steht. Als sich der Astronom Marshall McCall von der York Universität in Toronto im Jahr 2014 die lokale Scheibe etwas genauer angeschaut hat, hat er aber noch etwas viel spannenderes entdeckt: „A Council of Giants“ lautet der vielversprechende Titel seiner Facharbeit, also das „Konzil der Riesen“.

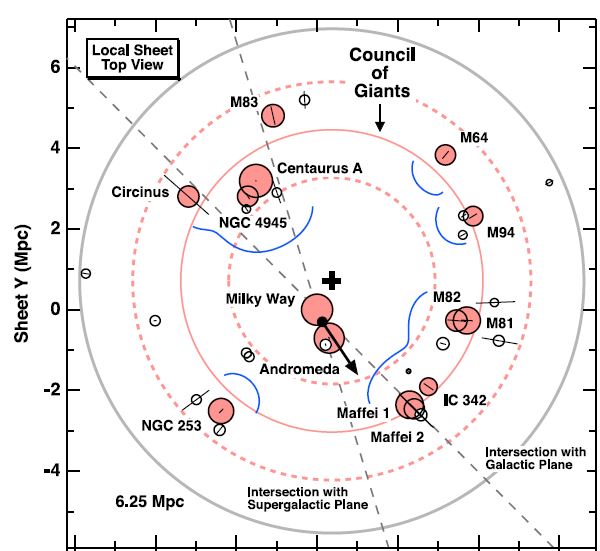
Schaut man sich die Abstände der hellsten Galaxien in der lokalen Scheibe in Bezug auf die Milchstraße bzw. die Lokale Gruppe an, stellt man etwas interessantes fest. Sie liegen immer zwischen 11 und 16 Millionen Lichtjahren. Oder anders gesagt: Die 12 hellsten und größten Galaxien der lokalen Scheibe bilden einen Ring um die Lokale Gruppe herum. Und so wie ein Konzil ja normalerweise gebildet wird, um wichtige Entscheidungen zu treffen, scheint auch das Konzil der Riesen bestimmt zu haben, was mit der Milchstraße passiert. Sie bilden quasi eine Grenze, die den gravitativen Einflussbereich der Lokalen Gruppe markiert. Und vielleicht sogar dafür gesorgt, dass sie überhaupt erst entstanden ist. McCall hat bei seiner Untersuchung herausgefunden, dass sich die Lokale Gruppe ziemlich genau dort befindet, wo sich die gravitativen Kräfte der Gruppe und der Galaxien des Konzils gegenseitig ausbalancieren. Der Einfluss der Galaxien im Konzil könnte dafür gesorgt haben, dass sich aus den Gasmassen im All die Galaxien der Lokalen Gruppe gebildet haben. Oder aber zumindest beeinflusst haben, wie die Galaxien der Lokalen Gruppe angeordnet sind. Dass zwei so große Galaxien wie die Milchstraße und die Andromeda genau im Zentrum des Galaxienrings und einander so nahe sind, dass sie in in ein paar Milliarden Jahren miteinander verschmelzen werden, kann Zufall sein. Es ist aber auch sehr unwahrscheinlich. Da wir bis jetzt nur eine lokale Scheibe im Detail beobachten können, ist es schwer, daraus allgemeine Regeln abzuleiten.
Aber die Angelegenheit ist auf jeden Fall spannend. Wir wissen immer noch nicht genau, wie das mit der Entstehung von Galaxien, Galaxiengruppen, Filamenten und so weiter wirklich abläuft. Nach den bisherigen Kenntnissen fängt alles mit dunkler Materie an. Von der gibt es im Universum deutlich mehr als von der normalen, sichtbaren Materie aus der Sterne, Planeten oder Menschen bestehen. Sehr viel mehr und im frühen Universum hat sie gigantische Wolke gebildet. Dort, wo diese Wolken am dichtesten waren, hat sich die normale Materie angesammelt, aus der dann Galaxien voller Sterne entstanden sind. Um so eine Konfiguration wie die lokale Scheibe, die Lokale Gruppe und das Konzil der Riesen zu erhalten, muss aber die dem ganzen zugrundeliegende lokale Ansammlung an dunkler Materie schon im Wesentlichen eine scheiben- bzw. filamentartige Struktur gehabt haben.
Wir werden unsere kosmische Nachbarschaft weiter untersuchen müssen. Oft es ist einfacher, in große Ferne zu schauen als die eigene Umgebung zu erkennen. Wir tun uns leichter, die Struktur des Universum auf großen Skalen zu kartografieren. So haben wir das irgendwie „schwammige“ Aussehen des Kosmos entdeckt; also die vielen Voids, die von Filamenten begrenzt sind. Das alles auch in unserer Nähe zu untersuchen ist schwieriger; hier müssen wir Abstände und Positionen viel genauer bestimmen, um ein vernünftiges Bild zu bekommen. Aber es sieht so aus, als wäre die Struktur des Universums auch im kleinen seinem großräumigen Verhalten ähnlich. Und wer weiß, ob in anderen Filamenten und Galaxienhaufen nicht auch noch ein paar Riesenkonzile zu finden sind…
Ich finde ja, der Artikel erklärt wirklich super verständlich und korrekt und ist zudem aus meiner Sicht sprachlich wirklich gut. Ich wünschte, ich könnte das auch nur annähernd.
Allerdings verstehe ich einige Aussagen nicht wie etwa:
„Die Erde selbst etwa, hat immer die gleiche Größe, die dehnt sich nicht aus“.
Nach dem Hubble-Gesetz müsste sich ein Pol der Erdoberfläche vom Mittelpunkt der Erde mit h*r = ca. 70 km/s/Mpc bei 12713.5km (Pol zu Pol) um ca. 1.44*10e-11 m/s entfernen, wenn man die Anziehungskräfte vernachlässigt – was hier zugegeben kaum zulässig sein dürfte. In jedem Fall, schon alleine weil die Hubble-Konstante gar nicht konstant ist, wären hier einige Integrale zu addieren. Ob da 0 rauskommt? „Unterhalb jeder Meßgenauigkeit“ dürfte die korrekte Aussage sein.
Hier also meine Frage: ist es nicht so, dass sich der Raum insgesamt ausdehnt, etwa so wie eine die Oberfläche eines 4-dimensionalen Luftballons? Anders kann ich mir nicht erklären, dass sich alle Galaxien voneinander entfernen.
Sorry für die Erbsenzählerei. Das soll sicher keine Kritik sein – ganz im Gegenteil! Es ist alles korrekt, soweit ich das verstehe.
Eine kurze Antwort dazu, ob und vielleicht wieso ich das falsch sehe, die wäre wirklich sehr nett. „Blumige Metaphern“ werden bei entsprechender Begründung kommentarlos akzeptiert.
@Joachim: Die Erde dehnt sich nicht aus, weil die Gravitationskraft ihrer Masse VIEL VIEL stärker ist als die Kraft der Expansion des Universums. Stell dir ein Gummiband vor, in dessen Mitte ein Stück Stahl eingebaut ist. Wenn du an den beiden Gummienden ziehst, dehnt sich der Gummi aus. Das Stück Stahl bleibt aber exakt gleich groß. So ist es auch mit der Erde und der Expansion des Alls. Nur auf sehr, sehr großen Skalen ist die Gravitationskraft schwach genug, um der Expansion nichts mehr entgegen setzen zu können.
@Joachim:
Das Hubble-Gesetz gilt nur auf ganz großen Skalen. Die Erde expandiert nicht.
Siehe https://math.ucr.edu/home/baez/physics/Relativity/GR/expanding_universe.html
Vielen Dank euch beiden. a) für den Link und b) für den Gummi-Stahl Vergleich (super Idee!)
Damit jetzt nicht „Why don’t you do your homework?“ kommt, mach ich das erst einmal vor möglichen weiteren Fragen.
@Joachim
Sehr gut. Dann kannst ja gleich mal loslegen.
Wie groß muss die Mindestentfernung zweier Galaxien mit
jeweils der Masse unserer Galaxie sein, damit die Expansion die Oberhand gewinnt.
Zum Vergleich: Die Andromedagalaxie ist 2,5 Millionen Lichtjahre entfernt. 😉
Hmm, ein Spiel? Okay.
Klar ist, Andromeda selbst macht Blauverschiebung. Es muss also mehr sein. Nehmen wir eine Rotation an?
@Joachim
Keine Rotation.
Der Drehimpuls müsste ja riesig sein, wenn Galaxien um einen zentralen Punkt rotieren.
Ist so was möglich?
r = 2*G*m / H^2
mit G = Gravitationskonstante, H = Hubble-Konstante, m = masse einer Galaxie und punktförmiger Massen
First guess, ohne Gewähr, ohne den Link zuende gelesen zu haben, im Kopf und sehr müde um 0:24.
Nich einmal nachgerechnet und auf Plausibilität geprüft.
@Joachim
Cool 🙂
Ich komme auf r^3 = 2*G*m / H^2.
Das wären dann, falls ich mich nicht verrechnet habe, 4,5 Millionen LJ. Ist diese Größenordnung plausibel?
@Karl-Heinz: Hoch 3, natürlich. Schäm. Vor (!) dem Nachschauen noch mal nachgerechnet.
Wenn 4.5e6 LJ der korrekten Formel entspringt, warum sollte das nicht plausibel sein? Ist deutlich weiter als M31…
@Joachim
Wenn es um eigene Ansätze geht, wo ich noch kein Beispiel im Netz gefunden habe, da bin ich immer vorsichtig. Zum Beispiel hatte ich im ersten Ansatz noch keinen Faktor 2 in der Formel. Und wie ich dann deine Formel mit der 2 gesehen habe, da sind mir fast die Augen rausgekullert.
Hast du die Formel selbst hergeleitet, oder irgendwo im Netz gefunden?
Ein Link dorthin wäre dann nett.
Kein Link. Das wäre doch ein schlechtes Spiel. Energien gleichgesetzt.
@Joachim
Ich nehme an du meinst, du hast die Beschleunigung gleichgesetzt. Ich habe gerade nachgedacht, ob der Ansatz kompliziert oder leicht ist. Eigentlich ist er einfach. Wenn man aber bestimmte Dinge nicht weiß, dann kann man unmöglich den Ansatz aufstellen. 😉
Gravitationsgesetz, Anziehung der Galaxien
F(r) := (G*m*m)/r^2
potentielle Energie aus der Gravitation
E_pot(r):=F(r)*r
Hubble-Gesetz
v(r):= H*r
kinetische Energie aus der Expansionsgeschwindigkeit und Masse
E_kin(r) := 1/2*m*v(r)^2
Mit E_pot(r)=E_kin(r) folgt
r^3 = 2*G*m/H^2
…
@Joachim
Da das nun geklärt ist, kannst Du gleich bei Goldbach weiter machen…
Wird ja nicht mehr allzu lange dauern, hoffe ich, und Thilo freut sich bestimmt auch schon drauf. 😉
@Joachim
r(t) = r0 * e^(H * t)
r'(t) =H * r0 * e^(H * t)
r“(t) =H^2 * r0 * e^(H * t)
Man beachte: bei t=0 gilt r‘ = H * r0
a= G * M / r^2
Ansatz: r“(t) = 2 * a für t=0
Da beide Galaxien mit der gleichen Beschleunigung a aufeinander zusteuern, wurde für die Gesamtbeschleunigung 2a gewählt.
r“(t) = 2 * a für t=0
H^2 * r0 = 2 * G * M / r0^2
r0^3 = 2 * G * M / H^2
PS: wie sieht’s mit Goldbach aus? Schon gelöst?
@stone1, das ist aber jetzt off topic. Das ist doch meine Domäne!
Ich habe mich entschlossen, erst einmal die Riemannsche Vermutung, du weißt, die mit den nicht trivialen Nullstellen der Zeta-Funktion, zu beweisen. Dann folgt Goldbach automatisch.
Nee, ernsthaft: die Beschäftigung mit diesen Dingen ist aussichtslos. Aber man lernt unglaublich viel dabei. Der Weg ist das Ziel. Mir ist egal, was jemand davon hält. Ich muss nichts beweisen.
Dagegen jedoch ist der „Beweis“ oben geradezu trivial, im Vergleich noch nicht einmal Physik-Abi Level (wenigstens bei uns damals). Der „Beweis“ ist, bis auf den dummen Fehler beim Kürzen, im Halbschlaf im Kopf durchführbar. Da ist gar nichts besonderes dran. Ich denke, Karl-Heinz wird mir da zustimmen.
Die Kunst ist es, erst einmal auf die Idee der Aufgabenstellung zu kommen. Dafür braucht es was. Genau deshalbt: wirklich vielen Dank Karl-Heinz. Es hat Spaß gemacht (und mich schlauer).
@Joachim
Ich fange mal damit an. Anschließend darfst du weiter machen. 🙂
Es ist zu zeigen, dass die Summe zweier ungerader Zahlen steht’s gerade ist.
n, m Element ℕ
ungerade: 2*n+1
ungerade: 2*m+1
Summe der beiden: 2*n+1 + 2*m+1 = 2*n + 2*m +2 =
2*n + 2*m +2 = 2 * (n + m +1)
Fazit: Summe der beiden kann durch zwei geteilt werden und damit ist die Summe zweier ungerader Zahlen steht’s gerade.
🙂 Ein Klassiker. 1. Semester Mathe.
Aber in der Binärdarstellung einer ungeraden Zahl ist die niederwertigste Stelle immer 1.
Beweis (verkürzt, wir sind ja nicht dumm):
sei a eine Zahl in Binärdarstellung beliebig.
2a ist per Definition a shift left 1. Folglich ist die niederwertigste Stelle von 2a = 0.
Bei 2a+1 ist die niederwertigste Stelle also 1.
Bei der Addition zweier Binärzahlen wird die niederwertigste Stelle also 0 mit Übertrag 1. Das ist eine gerade Zahl.
Das war zwar ein wenig schlampig, aber letztlich mit ein paar Ergänzungen korrekt. Leider ist der Heftrand hier etwas klein für einen Beweis 😉
Wenn du willst, es gibt sicher 4.5e6 Beweise dafür.
Zum Thema:
Die Summe zweier ungerader (Prim-) zahlen p1, p2 ist immer gerade, hat die Form 2n. Folglich existiert n als Zahl in der Mitte zwischen p1 und p2.
Weil p1 + p2 = 2n
=> (p1+p2)/2 = n (Mittelwert!)
Es existiert also ein d wo gilt:
p1 + d = n und p2 – d = n bzw.
p1 = n – d und p2 = n + d.
Soweit trivial.
p1 und p2 besitzen als Primzahlen natürlich keine Teiler.
Deshalb müssen n und d also Teilerfremd sein (trivial, sonst könnte man den Teiler ausklammern und damit müsse p1 und p2 diesen Teiler haben und wären keine Primzahlen.
Was hilft das? Nun, wir schlagen uns nicht mehr mit zwei Primzahlen rum sondern nur noch mit einem d.
Über d wissen wir also, dass es zu n (und damit auch zu 2n) teilerfremd ist.
Und nun kann es losgehen… (mit dem auf die Nase fallen).
@Joachim
Jetzt hab ich extra ausnahmsweise einen gelben Zwinkersmiley gemacht, was sonst nicht meine Art ist, um den Scherz zu kennzeichnen. Aber mit dem OT hast Du recht, sorry.
@Joachim
Und dabei sieht die Goldbachsche Vermutung so harmlos aus. 🙂
Ja. Aber da ist noch eine ganze Menge.
Bis von 3..9 sind alle ungeraden Zahlen Primzahlen.
Von 3..16 fast auch. Die blöde 15 ist durch 3 Teilbar, fällt also „aus dem Rahmen“
von 3..25 fallen alle ungeraden und durch 3 oder durch 5 teilbare Zahlen raus.
TL;DR: zwischen 3..k^2 gibt sind alle Zahlen prim oder durch die Primzahlen zwischen 3 und k teilbar.
Beweis?
@Joachim
k=4
Bereich: 3..k^2 = 3;4;5; … 10; … 16
Bereich: 3..k = 3;4
10 ist keine Primzahl und auch nicht durch 3 teilbar
10 ist gerade.
@Joachim
Allgemein gilt:
a, b und k > 0
a * b = k^2 = k * k
(a/k) * (b/k) = 1
Wenn zum Beispiel a größer als k ist, dann muss b kleiner als k sein damit die Multiplikation wieder 1 ergibt.
Also entweder ist deine ungerade Zahl eine Primzahl oder sie setzt sich aus zwei Faktoren zusammen, wobei ein Faktor immer kleiner gleich k und der andere Faktor immer größer gleich k ist. Der kleinere Faktor kann so gewählt werden, dass es sich um eine Primzahl handelt.
Beispiel: 3 * 5 * 7 = 105
105 ist keine Primzahl
Wurzel aus 105 =10,246…
Der kleinere Faktor muß kleiner gleich 10 sein.
Also 3 oder 5.
3 * 35 = 105
oder
5 * 21 = 105.
Man beachte, dass der zweite Faktor in diesem Fall immer größer gleich =10 ist.
Upss. Der zweite Faktor muss natürlich größer gleich 11 sein.
Bevor ich hier noch weiter was sage, @Florian Freistetter: Wir treiben hier gerade gewissermaßen fachfremden „Unsinn“ per Definition in deinem Blog und Forum. Das noch nichtmal mit der geringsten Aussicht auf ein sinnvolles Ergebnis.
Dies hier ist aber ein wissenschaftlicher Blog und kein Kindergarten.
Das geht also gar nicht und interessiert wahrscheinlich auch sonst niemanden.
Entweder verziehen wir uns irgendwo anders hin oder tauschen zunächst irgendwie die Mailadressen aus. Und wir bitten Florian Freistetter um Entschuldigung.
Sorry Karl-Heinz. Ich hätte es nicht zulassen dürfen, dass dies so ausartet. Mein Fehler. Ich muss wirklich sehr viel mehr aufpassen oder mal die Klappe halten.
Ja. Oder einfacher es gilt: k*(k+o) > k² mit o>1 (trivial)
Damit für a*b mit b=k+o eine Zahl <k² heraus kommt muss a < k sein.
Aber müssen wir nicht mal zunächst Florian Freistetter fragen, ob wir diesen "Unsinn" hier veranstalten dürfen? Ich finde das ihm gegenüber nicht fair.
Ich dachte, ich hätte sowas schon abgeschickt bzw gefragt? Komisch.
@Joachim
Platz für fachfremden und sonstigen Unsinn ist im offenen Laberthread bei blooDNAcid (aktuell OLT 28).