 Das ist die Transkription einer Folge meines Sternengeschichten-Podcasts. Die Folge gibt es auch als MP3-Download und YouTube-Video. Und den ganzen Podcast findet ihr auch bei Spotify.
Das ist die Transkription einer Folge meines Sternengeschichten-Podcasts. Die Folge gibt es auch als MP3-Download und YouTube-Video. Und den ganzen Podcast findet ihr auch bei Spotify.
Mehr Informationen: [Podcast-Feed][iTunes][Bitlove][Facebook] [Twitter]
Über Bewertungen und Kommentare freue ich mich auf allen Kanälen.
—————————————————————————————
Sternengeschichten Folge 398: Nichteuklidische Geometrie und die Form des Universums
Heute geht es in den Sternengeschichten um nichteuklidische Geometrie. Und weil das etwas kompliziert und abschreckend klingt habe ich auch gleich im Titel dazu gesagt, warum das für die Astronomie relevant ist. Nämlich wenn man wissen will, welche Form das Universum hat. Das IST mit Sicherheit eine sehr spannende Frage und die nichteuklidische Geometrie ist übrigens auch ziemlich cool!
Bevor wir zur nichteuklidischen Geometrie kommen müssen wir aber zuerst mal über die euklidische Geometrie reden. Die heißt deswegen so weil sie der griechische Mathematiker Euklid von Alexandria im 3. Jahrhundert vor Christus erfunden hat. Beziehungsweise hat er sie sicherlich nicht im Alleingang gefunden. Sondern das aufgeschrieben, was damals über Geometrie bekannt war. Aber er hat es auf eine ganz besondere Weise aufgeschrieben. Er hat nicht nur das bestehende Wissen zusammengefasst und systematisiert. Sondern auch gezeigt, wie Wissenschaft eigentlich laufen muss. Sein berühmtes Werk „Die Elemente“ war nicht einfach nur eine Auflistung von Dingen die man wusste oder glaubte zu wissen. Es ging Euklid darum, all dieses Wissen auch streng mathematisch zu beweisen. Also logisch einwandfrei aus bestehendem Wissen abzuleiten. Damit das funktioniert muss man sich aber erstmal auf etwas einigen, das zweifelsfrei richtig ist. Beziehungsweise so fundamental, dass man es nicht extra beweisen muss.
Euklids Buch – das übrigens auch heute noch erhältlich ist und seit seiner Entstehung 2000 Jahre lang als Lehrbuch benutzt wurde – ist nicht nur ein absoluter Klassiker. Sondern beginnt nach ein paar allgemeinen Definitionen darüber, was zum Beispiel ein Punkt oder eine Linie ist, mit fünf Postulaten. Das sind genau die Aussagen, die das Fundament des restlichen Buches bilden. Also das, was ohne Beweis von Anfang an festgelegt wird und aus dem der ganze Rest dann abgeleitet wird.

Im ersten Postulat behauptet Euklid dass man von jedem Punkt nach jedem Punkt eine Linie ziehen kann. Darauf kann man sich tatsächlich ohne großen Streit einigen; dass man eine Linie zwischen zwei Punkten ziehen kann muss man wohl nicht wirklich extra beweisen. Das zweite Postulat sagt, dass man eine begrenzte gerade Linie zusammenhängend gerade verlängern kann. Oder anders gesagt: Wenn ich eine kurze Linie zeichne, kann ich die kurze Linie auch einfach verlängern. Wird auch keinen großen Widerspruch hervorrufen, ebenso wie Postulat Nummer 3: Hat man einen Punkt und gibt einen Abstand von diesem Punkt vor, kann man einen Kreis zeichnen. Postulat Nummer 4 lautet: Ein rechter Winkel ist jedem anderen rechten Winkel gleich. Dass man keine zwei rechten Winkel haben kann, die nicht gleich sind wird wohl auch niemand bestreiten. Bei diesen ersten vier Postulaten ist alles mehr als klar. Niemand würde auf die Idee kommen, Euklid hier zu widersprechen. Das sind wirklich extrem fundamentale Aussagen über die Geometrie. Wenn man sich darauf nicht einigen und sie ohne Beweis als wahr ansehen kann, dann ist sowieso alles verloren. Bleibt noch Postulat Nummer 5. Darin fordert Euklid, „dass, wenn eine gerade Linie beim Schnitt mit zwei geraden Linien bewirkt, dass innen auf derselben Seite entstehende Winkel zusammen kleiner als zwei rechte Winkel werden, dann treffen sich die zwei geraden Linien bei Verlängerung ins Unendliche auf der Seite, auf der die Winkel liegen, die zusammen kleiner als zwei rechte sind“. Hu – das klingt auf einmal gar nicht mehr so simpel. Da muss man schon ein wenig nachdenken um überhaupt zu verstehen was gemeint ist. In einer kurzen Version meint Euklid hier: Hat man eine Linie die durch einen Punkt verläuft, und macht man dann noch einen Punkt irgendwo hin, der nicht auf der Linie liegt, dann kann man durch diesen zweiten Punkt zwar jede Menge unterschiedliche Linien ziehen. Aber nur eine einzige dieser Linien wird exakt parallel zur ursprünglichen Linie verlaufen. Ist immer noch ein wenig kompliziert. Wir können auch diese Version probieren: Zu jeder Linie kann man nur genau eine einzige parallele Linie zeichnen. Aller anderen Linien schneiden sich irgendwann immer.
Jetzt versteht man zwar was Euklid damit meint. Aber unbefriedigend ist das irgendwie immer noch. Zuerst vier so kurze, leicht verständliche und sehr offensichtlich richtige Postulate. Und dann dieses seltsame fünfte Postulat, dass alles andere als kurz, elegant und leicht verständlich ist. Und im Gegensatz zu den restlichen vier ist auch absolut nicht offensichtlich, dass es ohne Beweis als richtig vorausgesetzt werden kann. Es sieht irgendwie so aus, als hätte Euklid es nicht geschafft zu beweisen, dass die Sache mit den parallelen Linien aus den ersten vier Postulaten logisch abgeleitet werden kann. Und es deswegen einfach ohne Beweis als fünftes Postulat hinzugefügt. Das dachten im Laufe der Zeit auch jede Menge Mathematikerinnen und Mathematiker. Und versuchten dieses hässliche „Parallenpostulat“ los zu werden. Aber alle scheiterten. Niemand war in der Lage nur mit den vier eleganten Postulaten zu beweisen, dass es zu jeder Linie nur genau eine parallele Linie gibt.
Es sah ganz so aus, als würde man dieses Parallelenpostulat halt brauchen, wenn man daraus all die Aussagen über die euklidische Geometrie beweisen wollte. Die euklidische Geometrie ist übrigens das, was normalerweise einfach nur „Geometrie“ heißt und was wir alle in der Schule lernen. Also der ganze Kram mit den gleichschenkeligen, gleichseitigen, rechtwinkeligen Dreiecken, mit den Kreisen, Quadraten, und so weiter. Die Sache mit den Parallelen hat den Leuten aber keine Ruhe gelassen. Es war aber schlicht und einfach kein Weg zu finden, dieses Postulat aus den anderen abzuleiten und zu beweisen. Und irgendwann kam man auf die Idee zu schauen, was denn eigentlich so passiert, wenn man aufhört es zu versuchen und stattdessen einfach mal so tut, als wäre es falsch. Beziehungsweise war das nicht „man“ und nicht irgendwann, sondern es war der große Mathematiker Carl Friedrich Gauß und es war im Jahr 1813. Unabhängig von Gauß hat das 1818 auch der Jurist und Mathematiker Ferdinand Karl Schweikart getan. Sie waren die ersten, die sich über eine nichteuklidische Geometrie Gedanken machten, also eine Geometrie in der das fünfte Postulat von Euklid nicht gilt. Und bevor ich erzähle, was das Resultat dieser Gedanken war, erwähne ich noch kurz, dass weder Gauß noch Schweikart ihre Ergebnisse öffentlich publiziert haben. Weswegen auch der russische Mathematiker Nikolai Iwanowitsch Lobatschewski nichts davon wusste als er 1829 seine Forschung zur nichteuklidischen Geometrie publiziert hat und auch der Ungar János Bolyai wusste nichts von Gauß und Schweikart und auch die Arbeit von Lobatschewski hat er nicht bemerkt, als er 1832 unabhängig von allen anderen ebenfalls eine nichteuklidische Geometrie entwickelt hat.
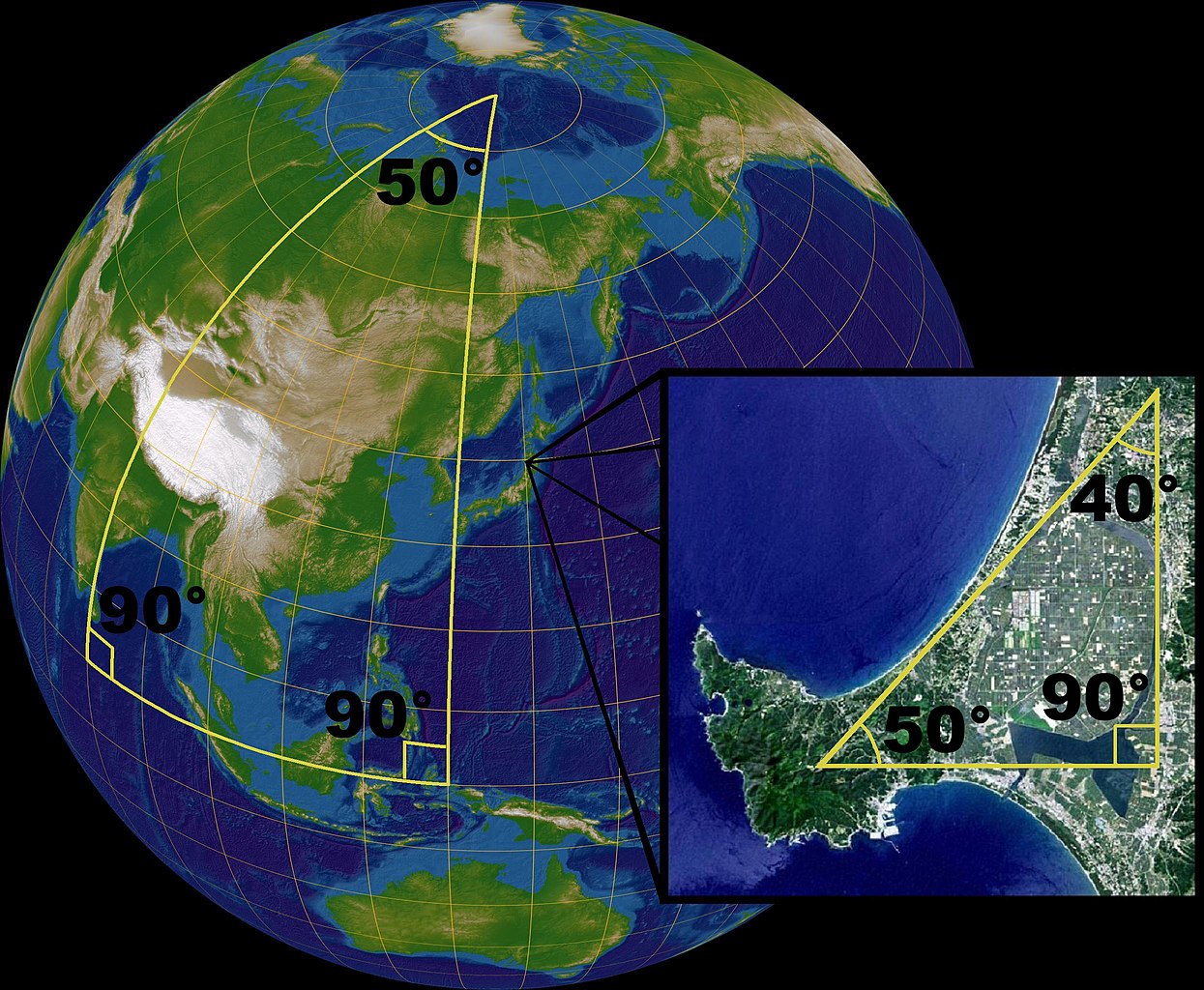
Aber egal wen man jetzt offiziell als Entdecker benennen will: Viel interessanter sind die Ergebnisse. Was passiert, wenn das fünfte Postulat nicht gilt? Dann kann man es auf zwei Arten ändern. Man kann zum Beispiel behaupten, dass man zu einer Linie keinen Punkt außerhalb der Linie finden kann, durch den eine parallele Linie verlaufen kann. Oder anders gesagt: Zwei Linien müssen sich IMMER schneiden; Parallelen existieren nicht. Das klingt ein wenig komisch. Ist es aber nicht. Man kann sowas leicht selbst erleben. Stellen wir uns vor, wir stehen genau auf dem Äquator der Erde. Und zeichnen eine Linie, die exakt von Nord nach Süd verläuft. Dann gehen wir den Äquator ein paar Kilometer entlang und zeichnen einen zweite Linie auf den Boden, die ebenfalls exakt von Nord nach Süd verläuft. Sind die beiden nun parallel oder nicht? Das können wir herausfinden, wenn wir die Linien länger machen. Wenn wir die erste Linie nach Norden verlängern läuft sie – wenig überraschend – immer weiter nach Norden. Bis sie irgendwann auf den Nordpol trifft. Exakt das gleich passiert aber auch mit er zweiten Linie! Die beiden Linien die am Äquator noch parallel ausgesehen haben, schneiden sich! Es gibt noch weitere seltsame Beispiele. Alle lernen in der Schule, dass die Summe der drei Winkel in einem Dreieck immer 180 Grad ergibt. Stellen wir uns jetzt aber mal gedanklich auf den Nordpol. Und laufen die vorhin gezogene Linie zum Äquator entlang. Dort drehen wir uns um einen Winkel von 90 Grad, spazieren am Äquator dorthin wo wir die zweite Linie gezeichnet haben und drehen uns ein weiteres Mal um 90 Grad zurück Richtung Norden. Jetzt laufen wir auf dieser anderen Linie zurück zum Nordpol, den wir aus einer anderen Richtung erreichen als wir ihn verlassen haben. Wir müssen uns also ein letztes Mal um einen bestimmten Winkel drehen bis wir wieder in der Ausgangssituation sind. Wie groß dieser letzte Winkel ist hängt davon ab, wo genau wir die Linien gezeichnet haben. Ist aber auch egal. Denn unser Weg ist exakt entlang der Seiten eines Dreiecks erfolgt und zwei der Winkel dieses Dreiecks waren rechte Winkel mit jeweils 90 Grad. Zusammen also schon 180 Grad und da kommt noch der dritte Winkel dazu. Die Winkelsumme in unserem Dreieck ist also definitiv größer als 180 Grad!
Was ist hier los? Nix außergewöhnliches. Nur dass die Erde eben eine Kugel ist und keine flache Scheibe. Und die euklidische Geometrie nur für die Ebene gilt. Und die Erdoberfläche mag uns zwar aus unserer menschlichen Sicht sehr flach erscheinen. In Wahrheit wohnen wir aber auf einer großen Kugel deren Oberfläche gekrümmt ist. Und wenn man die Geometrie auf einer gekrümmten Fläche beschreiben will, braucht man eine nichteuklidische Geometrie, wo sich parallele Linien schneiden können und die Winkelsumme von Dreiecken größer als 180 Grad ist. Will man den Umfang eines Kreises auf einer gekrümmten Oberfläche berechnen ist der kleiner als das, was wir mit der üblichen Formel von U=2rpi berechnen und so weiter. Es ist eine andere Geometrie als die von Euklid, aber immer noch eine in sich logische Geometrie mit ihren eigenen Regeln. Die Krümmung der Erdoberfläche ist aber nur eine der beiden möglichen Krümmungen. Man kann das fünfte Postulat auch so ändern, dass man durch einen Punkt der nicht auf einer Linie liegt, mindestens zwei zur ersten parallelen Linie ziehen kann. Auch daraus leitet sich eine komplette nichteuklidische Geometrie ab, hier haben Dreiecke eine Winkelsumme von weniger als 180 Grad, der Umfang eines Kreises ist größer als 2rpi und so weiter. Eine gekrümmte Oberfläche auf der diese Regeln gelten kann man sich nicht mehr so leicht vorstellen wie die Erdoberfläche. Aber man kann sich zum Beispiel einen Sattel vorstellen. Oder, wer keinen Bezug zu Pferden hat, einfach einen Pringles-Chip, der ja auch wie ein Sattel gekrümmt ist. Genau diese Art von gekrümmter Oberfläche ist es, auf der die zweite Variante von nichteuklidischer Geometrie gilt.
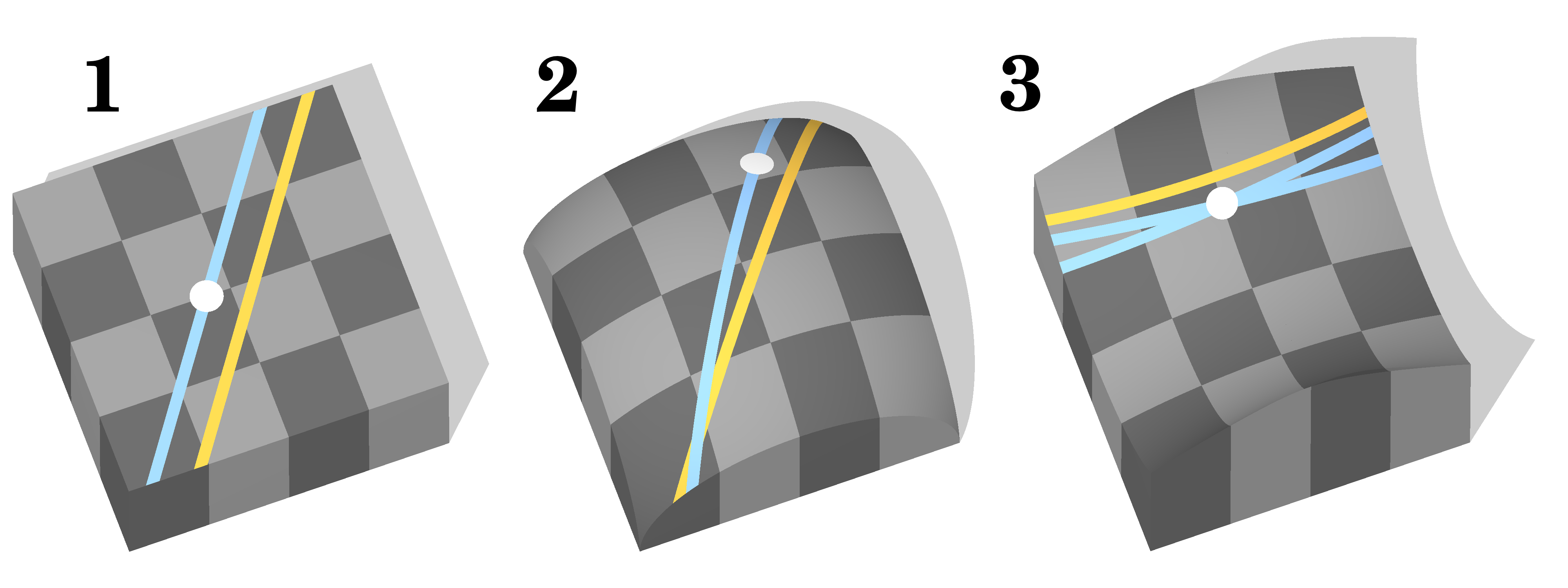
Die erste nennt man „elliptische“ oder „sphärische Geometrie“, die zweite „hyperbolische Geometrie“ und die ursprüngliche, die „normale“ Geometrie wird als „flache Geometrie“ oder eben „euklidische Geometrie“ bezeichnet. In der Mathematik hat man es ständig mit nichteuklidischer Geometrie zu tun, ihre Entdeckung war enorm wichtig. Aber ich habe ja zu Beginn angekündigt dass ich auch noch von der Form des Universums reden werde.
Hier wird es jetzt noch ein kleines bisschen schwieriger sich alles anschaulich vorzustellen. Die Erdoberfläche ist zweidimensional. Die Erde selbst ist natürlich eine dreidimensionale Kugel. Aber ihre Oberfläche ist eben nur eine zweidimensionale Fläche. Die gekrümmt ist, im Gegensatz zu einer nicht gekrümmten zweidimensionalen Fläche. Man kann sich das ganz einfach mit einer Landkarte und einem Globus vorstellen. Die Landkarte ist zweidimensional und flach. Ich kann sie problemlos flach auf den Tisch legen. Aber so sehr ich mich auch anstrege, ich werde es nicht schaffen, die Landkarte ohne Falten, Zerreißen oder andere Eingriffe flach um den Globus herumzulegen. Ein Problem das auch alle kennen die schon mal probiert haben einen Ball in Geschenkpapier einzupacken. Eine flache Fläche ist fundamental anders als eine gekrümmte Fläche und ich kann die eine nicht in die andere verformen. Für eine hyperbolisch gekrümmte Fläche gilt das alles übrigens genau so. Beim Universum haben wir es jetzt aber nicht mehr mit einer Fläche zu tun. Der Raum ist dreidimensional. Kann aber trotzdem gekrümmt sein. Das war ja die große Erkenntnis von Albert Einstein und seiner Relativitätstheorie: Masse krümmt den Raum und diese Krümmung im Raum nehmen wir als Gravitationskraft war. Es ist also auch nicht verwunderlich, dass man es mit nichteuklidischer Geometrie zu tun bekommt, wenn sich mit Einstein und der Gravitation beschäftigt.
Die durch die Massen im Raum verursachten Krümmungen sind aber nicht das, was uns im Moment interessant. Das sind quasi kleine Störungen. Genau so wie ja auch auf der Oberfläche der Erde Berge und Täler existieren, Löcher, Gräben und jede Menge andere geografische Eigenheiten die von der idealisierten gekrümmten Kugeloberfläche abweichen. Wir wollen wissen: Welche Form hat das Universum in seiner Gesamtheit? Oder anders gefragt: Welche Geometrie braucht man, wenn man das Universum als ganzes beschreiben will? Ich könnte jetzt noch fragen ob das Universum flach oder kugelförmig ist, aber das würde falsche Vorstellungen wecken. Wir reden hier von einem gekrümmten dreidimensionalen Raum und das können wir uns nicht mehr anschaulich vorstellen. Ein dreidimensionaler gekrümmter Raum wäre zum Beispiel die „Oberfläche“ einer vierdimensionalen Kugel. Aber niemand kann sich eine vierdimensionale Kugel vorstellen und auch nicht ihre dreidimensionale Oberfläche. Bleiben wir daher bei der etwas abstrakteren Frage: Wenn ich die Geometrie im Universum richtig beschreiben will: Muss ich dann die Formeln der flachen Geometrie nehmen, die der sphärischen wo die Dreicke mehr als 180 Grad als Winkelsumme haben oder die hyperbolische Geometrie mit weniger als 180 Grad? Damit zusammen hängt auch die Frage ob das Universum unendlich oder endlich groß ist. Ein Universum mit sphärischer Geometrie hat nur ein endlich großes Volumen. Ein Universum mit flacher oder hyperbolischer Geometrie kann sowohl endlich als auch unendlich groß sein.
Es hilft leider auch nichts, irgendwo riesige Dreiecke ins All zu zeichen. Beziehungsweise es würde helfen, wenn sie WIRKLICH groß werden, einmal halb durchs beobachtbare Universum oder so. Aber das können wir nicht. Wir können aber indirekte Messungen anstellen die uns ein bisschen was darüber verraten, ob und wie der Kosmos gekrümmt ist. Man kann einerseits die kosmische Hintergrundstrahlung messen, von der ich in Folge 316 mehr erzählt habe. Das ist Strahlung, die aus allen Richtungen auf die Erde trifft und kurz nach dem Urknall entstanden ist. Sie war quasi durch das gesamte beobachtbare Universum unterwegs und wenn man die genau genug untersucht kann man – mit Methoden auf die ich jetzt nicht im Detail eingehen will – abschätzen wie das Universum gekrümmt ist. Andererseits kann man probieren möglichst genau zu messen, wie viel Masse und Energie im beobachtbaren Universum vorhanden ist. Denn dieser gesamte Masse/Energiehaushalt bestimmt ja auch die Krümmung des Raums. Beides hat man gemacht und innerhalb der Meßgenauigkeit – die leider nicht extrem genau ist – lautet das Ergebnis: Unser Universum ist flach! Die mehr als 2000 Jahre alte Geometrie von Euklid mit ihrem komischen fünften Postulat ist genau die Geometrie die man braucht um das Universum zu beschreiben.

Bild: Pablo Carlos Budassi, CC-BY-SA 3.0
Das muss aber leider noch nicht die definitive Antwort sein. Erstens müssen wir noch viel genauer messen. Und zweites können wir ja nur Aussagen über das beobachtbare Universum machen. Also von all den Regionen des Kosmos aus denen das Licht in den letzten 13,8 Milliarden Jahren seit dem Urknall Zeit hatte, bis zu uns zu kommen. Das gesamte Universum kann aber sehr viel größer sein als dieser für uns sichtbare Bereich. Und vielleicht erscheint uns unser beobachtbares Universum nur flach, genau so wie uns die Oberfläche der Erde flach erscheint, weil wir viel zu klein sind um sie als die enorme Kugel wahrzunehmen die sie ist.
Welche Form das Universum hat, ist eine der großen offenen Fragen in der Naturwissenschaft. Aber zumindest haben wir die Sache mit diesem nervigen fünften Postulat geklärt!
Hallo,
zur dem Thema schwirren mir immer einige Fragen durch den Kopf.
1) Oft ist von einen „Kruemmungsfaktor“ die Rede.
Der kann dann einen Wert von „stark hyperbolisch“->“schwach hyperbolisch“->“flach (euklidisch)“,->“schwach spaerisch“ -> „stark spaerisch“ annehmen. (Irgendeine einfache Zahl also, die bei „flach“ einen besonderen Wert annimmt).
Wie genau ist diese Zahl definiert?
2) Wenn ich eine „beulenfoermige“ Geometrie habe (z.b. eine starke Kruemmung um eine Gravitationsquelle herum,- aber eben nur dort und nicht ueberall) -> Dann muesste an jeden Punkt des Raumes dieser „Kruemmungsfaktor“ anders sein. Ich muesste also irgendein Feld haben, bei dem an jedem Punkt des Raumes ein anderer Kruemmungsvektor aufgefuehrt ist.
Wie schreibt man das formal hin,- und wie schreibt man eine solche Formel um fuer jeden Punkt einen solchen Faktor zu berechnen?
Bei der Frage geht es mir um den Formalismus,- nicht um das Prinzip, dass es ein solches Feld gibt.
(Oder ist der Formalismus ganz anders,- und ich habe einen Denkfehler)
3) Wie genau ist „eine Grade“ definiert?
Wenn ich eine Linie mit einen Linieal verlaengere, dann kann ich das auf einen flachen Stueck Papier machen. Auf einer Kugel werde ich mit meinen graden Lineal aber Schwierigkeiten haben, weil das Lineal immer „wackeln wird“ und niemals komplett auf der runden Kugel aufliegen wird.
Die Definition „grade ist was sich grade anfuehlt“ ist irgendwie unbefriedigend.
Im 3Dimensionalen Raum wird das Problem noch problematischer,- da ich mir kein Werkzeug vorstellen kann was nicht seinerseits auch der Kruemmung unterliegt, wenn es in den gekruemten Raum benutzt wird.
4) In mehrdimensionalen Raeumen:
Gibt es Geometrien wo eine Dimension flach,- aber die naechste Dimension spaerisch ist?
Oder wo der Kruemmungsfaktor fuer jede Dimensionsrichtung anders ist.
(z.b. Die Oberflaeche eines Ellipsoid, wo in eine Richtung der Umgfang groesser ist als in die andere Richtung)
Wie sieht das im 3Dimensionalen aus?
@Ingo:
Diese Frage haben sich viele Leute gestellt. Du bist da in guter Gesellschaft. Die Antwort kommt von Einstein und ist sowohl erstaunlich als auch knifflig:
eine Gerade ist der Weg, dem ein Lichtstrahl folgt.
Pervers ist in diesem Fall, daß du vielleicht einwenden magst, daß Lichtstrahlen sehr wohl krümmbar sind – durch große Massen zum Beispiel. Einstein konnte aber zeigen, daß dies ein Irrtum ist: der Weg entlang eines Lichtstrahls ist immer der kürzeste zwischen zwei Punkten, und wenn du den als „gekrümmt“ wahrnimmst, dann ist deine Wahrnehmung unzutreffend, weil euklidisch. 🙂
@Bullet #2:
Genau das Problem meine ich.
Bei Einstein spricht man immer von den „Geodaeten“ (der kuerzesten Verbindung von A nach B).
Aber wie genau ist die definiert?
Man koennte nun agumentieren wie „das Licht nimmt jeden theoretisch moeglichen Weg, aber nach Feynman interferieren sich alle Wege weg, und nur der kuerzeste bleibt ueber“.
Aber das hiesse mathematisch nichts weiter als „man misst alle Entfernungen aus, und schaut nach welcher weg der kuerzeste ist“
Damit ist aber immer noch nicht definiert wie die Grade ueber A oder B hinaus weiter gehen wuerde.
(Eine Grade ist unendlich lang, und keine endliche Strecke von A nach B)
@Ingo: Was du suchst ist vielleicht das mathematische Prinzip der „kleinsten Wirkung“: https://www.spektrum.de/kolumne/die-regel-der-die-welt-gehorcht/1734972
@Ingo:
zu (1): Den Begriff „Krümmungsfaktor“ kenne ich so nicht – hast du vielleicht ein, zwei Quellen, wo der vorkommt? Meinst du vielleicht den Riemann’schen Krümmungstensor, oder den Ricci-Tensor, oder den Krümmungsskalar?
zu (2): Zu den drei Begriffen, die ich genannt habe, gibt es Formeln. Findet man auch leicht im Internet, z. B. bei Wikipedia.
zu (3): Statt „Gerade“ müsste man „Geodäte“ sagen, wie ja schon angemerkt wurde. Mathematisch kann man sich diese herleiten, indem man für gegebene (Vierer-)Geschwindigkeit die Bahn sucht, auf der sich ein Körper in kürzester Eigenzeit vom einen Punkt zum anderen bewegt. Man kommt dann zur passend benannten Geodätengleichung. (Auch hier wieder: siehe z. B. Wikipedia.) Und so eine Geodäte ist dann auch nur auf eine Weise eindeutig bis ins Unendliche fortsetzbar.
zu (4)
Gibt es sicher. Verwendet z. B. die Stringtheorie, da sind ja ein paar der räumlichen Dimensionen „aufgerollt“. (also eher kreisförmig als sphärisch, aber das hast du wohl gemeint?)
Dafür braucht man eben die oben erwähnten Tensoren. 😉
Wenn du eher an der mathematisch-geometrischen Vorstellung interessiert bist, dann würde ich dir das Buch „The shape of space“ von Jeffrey Weeks sehr empfehlen. Wenn dich die konkrete rechnerische Behandlung dieses Themas interessiert, dann solltest du definitiv in „Isaac oder die Entdeckung der Raumzeit“ von Martin Bäker reinschauen. (Der ja auch hier bei den Scienceblogs schreibt.)
@Ingo könnte auch einfach die schöne Serie von Martin Bäker lesen:
Wie man den Raum krümmt.
@Ingo
Zu 1:
Man kann die Krümmung so definieren, dass man am jeweils betrachteten Punkt zwei Kreise anpasst, die sich dort quasi „anschmiegen“ (dazu muss man sich das ganze „eingebettet“ in eine höhere Definition vorstellen; mathematisch geht es auch ohne, das ist aber nicht so anschaulich.)
Die Krümmung ist dann das Produkt aus dem Kehrwert der beiden Radien; liegen die beiden Kreise auf entgegengesetzten Seiten der Fläche wie bei einem Sattel, dann ist die Krümmung negativ.
Siehe auch Wikipedia unter Gaußsche Krümmung
Trickreich (jedenfalls, wenn man in die Bücher zur ART guckt) ist, dass die Krümmung gern so umnormiert wird, dass man nur noch drei mögliche Werte hat, +1 (für Kugelartig) 0 (für flach) und -1 (für hyperbolisch=sattelförmig). Das hat mich lange Zeit extrem verwirrt, weil es da scheinbar keinen stetigen Übergang gibt, das liegt aber nur an einer trickreichen mathematischen Normierung.
Zu 2: Dafür gibt es den Riemannschen Krümmungstensor, der enthält 20 Zahlen (in 4 Dimensionen für die Raumzeit), die genau das beschreiben.
Zu 3: Eine Gerade ist die kürzeste Verbindung zwischen zwei Punkten – also auf dem globus ein Stück eines Großkreises. In der Raumzeit ist eine Gerade definiert über eine Linie maximaler Eigenzeit.
Dass die Werkzeuge selbsta uche iner Krümmung unterliegen, macht das ganze in der Tat sehr trickreich, es gibt aber clevere mathematische Tools (z.B. den Paralleltransport), mit denen man das trotzdem fassen kann. grundprinzip dabei ist immer, dass in einer hinreichend kleinen Umgebung eines Punktes die Raumzeit flach ist.
4. Ja, klar, so etwas kann es geben. Wobei das dadurch trickreicher wird, dass es natürlich vom Koordinatensystem abhängt, welche Dimension welche ist. Ein Beispiel ist die gekrümmte Raumzeit um eine Masse – in geeigneten Koordinaten ist da der Raum vollkommen flach. (Ändert an der Physik aber nichts).
Alle diese Dinge erkläre ich übrigens sehr detailliert in meinem Buch, das beantwortet genau diese Fragen sehr ausführlich
https://scienceblogs.de/hier-wohnen-drachen/2019/01/29/hallo-isaac-mein-buch-ist-da/
Zu (1)
Bjoern #5
> Den Begriff „Krümmungsfaktor“ kenne ich so nicht
> – hast du vielleicht ein, zwei Quellen, wo der
> vorkommt? Meinst du vielleicht den Riemann’schen
> Krümmungstensor, oder den Ricci-Tensor, oder
> den Krümmungsskalar?
Nein,- solche Quellen habe ich nicht.
Ich habe ehrlich gesagt keine Ahnung und auch keinen echten mathematischen Hintergrund .
Ich habe nur folgende Ueberlegung:
„Wenn ich irgendwie die Geometrie beschreiben moechte,- dann muss ich dies in irgendeiner Weise mit irgendeiner Zahl/Vekor/Tensor/Feld/Was auch immer machen.
Anhand dieses Wertes sollte man dann erkennen koennen wie die Geometrie geformt ist,- und beispielsweise errechnen koennen „wie weit ich auf der Kugelobeerflaeche laufen muss um wieder dort anzukommen wo ich war“ (in dem Fall identisch mit dem Umfang der Kugel),- oder ich muesste ausrechnen koennen wie schnell sich zwei angfaenglich parallele Graden sich voneinander entfernen, wenn ich sie fortfuehre (im Falle einer hyperbolischen Geometrie)“
Ich vermutete einfach dass es eine solche Zahl/Vektor/Tensor/Feld in irgendeiner Weise gibt,- und wollte wissen wie er heisst, damit man sich mit dem entsprechenden Suchbegriff etwas besser einlesen kann.
Martin #7:
> Trickreich (jedenfalls, wenn man in die Bücher
> zur ART guckt) ist, dass die Krümmung
> gern so umnormiert wird, dass man nur noch drei
> mögliche Werte hat, +1 (für Kugelartig)
> 0 (für flach) und -1 (für hyperbolisch=sattelförmig).# > Das hat mich lange Zeit extrem
> verwirrt, weil es da scheinbar keinen stetigen
> Übergang gibt
Genau das hatte mich auch verwirrt.
Schliesslich muesste man wieder „Zahl“ irgendwie ansehen koennen „wie gross die Kugel ist,- oder wie eng der Sattel“.
> Die Krümmung ist dann das Produkt aus dem
> Kehrwert der beiden Radien;
> liegen die beiden Kreise auf entgegengesetzten
> Seiten der Fläche wie bei
> einem Sattel, dann ist die Krümmung negativ.
> Siehe auch Wikipedia unter Gaußsche Krümmung
Das Stichwort hat etwas weiter geholfen. Danke.
Es scheint die Geometrie aber nicht vollstaendig zu beschreiben. Der Wiki-Link sagt zum Beispiel, dass die Oberflaeche eines Kegel und ein Zylinder beide „0“ haben,- wobei das insofern auch bildlich nachvollziehbar ist, da sich beide Objekte aus einen flachen Stueck Papier konstruieren lassen.
In dem Fall haette aber auch eine „aufgerolte Dimension“ wie in der Stringtheorie die Gaussche Kruemmung 0. Es wuerde sich anhand des Wertes nicht erkennen lassen „wie weit man gehen muss um wieder da anzukommen wo man losgelaufen ist“
Zu (2)
Martin #7
> Dafür gibt es den Riemannschen
> Krümmungstensor, der enthält 20
> Zahlen (in 4 Dimensionen für die Raumzeit), die
> genau das beschreiben.
Er beschreibt aber nur einen Punkt soweit ich das verstehe.
Um die gesamte „Beulenfoermige“ Geometrie zu beschreiben, braeuchte man dann ein Feld.
Spaetestens wenn es mehrere „Beulen“ gibt (z.b. mehrere Sterne) muesste all diese Information in die gesamte Beschreibung einfliessen.
Zu (3)
Bjoern #5
> Und so eine Geodäte ist dann auch nur auf eine
> Weise eindeutig bis ins Unendliche fortsetzbar.
Manchmal braucht es nur einen Satz, der einen Knoten aufloesst. Danke 🙂
Ich dachte bisher faelschlicherweise dass eine Geodaete nur als die kuerzeste (endliche) Strecke von „A“ nach „B“ definiert ist.
Sie geht aber bis ins unendliche weiter. Eigentlich haette ich da auch alleine drauf kommen koennen,- schliesslich hat eine Kreisbahn (als Fall einer Geodaete) auch kein Anfangspunkt und Endpunkt.
@PDP10 #7
> einfach die schöne Serie von Martin Bäker lesen
> „Wie man den Raum krümmt“
Ich werde sie nochmal lesen. Ist schon einige Zeit her dass ich sie gelesen hatte. Wie das so ist,- erst durch wiederholtes Lesen wird man klueger 🙁
@Ingo
„Genau das hatte mich auch verwirrt.
Schliesslich muesste man wieder “Zahl” irgendwie ansehen koennen “wie gross die Kugel ist,- oder wie eng der Sattel”.“
Ja, da wird geschickt so umnormiert, dass nur diese drei Werte möglich sind. Kann man ein bisschen im ART-Skript von Carroll nachvollziehen, da wird das zumindest halbwegs erklärt; ich habe es auch in meinem buch irgendwo in den technischen Anmerkungen erläutert.
„Er beschreibt aber nur einen Punkt soweit ich das verstehe.“
Oh, das hatte ich nicht geschrieben, sorry: Der krümmungstensor ist ein feld, er ist also an jedem Puntk definiert und kann an jedem Punkt andere Werte haben. Du musst also jedem Punkt der Raumzeit 20 Zahlen zuordnen.
„In dem Fall haette aber auch eine “aufgerolte Dimension” wie in der Stringtheorie die Gaussche Kruemmung 0. “
Man muss zwischen „intrinsischer“ und „extrinsicher“ Krümmung unterscheiden – wenn ich eine Flache Dimension nur aufrolle, dann ist sie zwar extrinsicht gekrümmt, aber nicht intrinisch. (Eine Ameise, die auf dem papeir lebt, merkt von der Krümmung nix, Dreiecke haben Winkelsumme 180 Grad etc. Rate mal, wo ich das ganz ausfürhlich erkläre…)
Mit dem Stringtheorie-Kram kenne ich mich nicht aus, aber wenn die die Dimensionen so aufrollen, ja, dann sind die nicht (intrinsisch) gekrümmt.
@Ingo u. MartinB
Danke für die Fragen und die Antworten. Auch ich hatte mir darüber Gedanken gemacht, wie kann man sich das Ganze vorstellen, ohne dass man jetzt zu tief in die Materie abtauchen muß.
Und Danke natürlich auch an Florian für diesen interessanten Artikel. 🙂
Interessant finde ich dabei auch die Grenzen unserer Vorstellungskraft, die keineswegs Schritt halten kann mit unserem mathematisch-abstrahierenden Denken.
Dass wir schon mit der vierten Dimension, also Zeit, ein Problem in der Visualisierung bekommen, ist bekannt und wir führen es darauf zurück, dass wir Zeit nicht als Dimension wahrnehmen, sondern als absolutes Kontinuum eigenständiger Art, losgelöst von Raum, was Einstein ja revidierte.
Dass wir uns fünf Dimensionen gar nicht mehr vorstellen können, ergibt auch noch Sinn, da wir nur unsere physisch erlebbaren drei wahrnehmen plus die Zeit. Dass wir uns umgekehrt zwei Dimensionen dennoch gut vorstellen können, obwohl sie ja eine Reduzierung und Abstraktion unserer dreidimensionalen Welt darstellen, ist auch noch verständlich – wegen unseres abstrakten Denkens, das wir operativ umsetzen können, z.B. eben in der Geometrie. Hauptsächlich aber wohl deswegen, weil es auf unsere Wahrnehmung zurück geht: Die Oberfläche einer Wand nehmen wir nur zweidimensional wahr, also akzeptieren wir das.
Aber warum haben wir wieder Probleme uns Eindimensionales vorzustellen? Einen Punkt zum Beispiel, denn der ist beliebig klein. Singularitäten also. Selbst wenn wir mit bloßem Auge zu fernen, kaum noch sichtbaren Sternen hinauf schauen, akzeptiert unser Hirn das Konzept „Ein-Dimensional“ nicht, wir „dichten“ automatisch eine Fläche hinzu, eine zweite Dimension. Das taten Menschen wohl schon, noch bevor sie wussten, was Sterne sind und dass sie mit ihrer zwei-, bzw. dreidimensionalen Annahme richtig lagen.
Es scheint so, als bräuchten wir mindestens 2, höchstens aber 3 Dimensionen, in denen unser Geist ohne Verrenkung arbeiten kann. 4 ist schon zu viel, 1 ist zu wenig. Und was ist mit 0 Dimensionen? Also der Ur-Frage was „vor“ dem Universum war? Genauso unmöglich für uns zu visualisieren, wie fünf Dimensionen, wenn nicht sogar noch schwerer.
Unser Gehirn, oder zumindest dessen visualisierender Teil, arbeitet also in einem „Was nicht passt, wird passend gemacht“-Modus noch aus der Steinzeit. Er ist streng „objektorientiert“, auch wenn dieser Begriff aus der Informatik nicht so ganz passt. Und er scheint nicht gekoppelt zu sein an das abstrakte Denkvermögen, wodurch Selbiges aber auch nicht von Ersterem profitieren kann. Vielleicht ändert sich das eines (fernen) Tages. Vielleicht können wir uns dann auch die Form des Universums vorstellen – inklusive der Zeit.
@Adam
Oh, … und ich dachte immer, dass
die euklidische Ebene die Dimension 2, die Zahlengerade die Dimension 1, der Punkt die Dimension 0 hat. 😉
@Karl-Heinz
Ja, da lag ich daneben. Interessant ist dann aber, weil der Punkt ja nicht nichts ist, dass noch nicht mal 0 Dimensionen für das „vorher“ gelten. Also wird es noch abstrakter 🙂