 Dieser Artikel ist Teil des ScienceBlogs Blog-Schreibwettbewerb 2017. Informationen zum Ablauf gibt es hier. Leserinnen und Leser können die Artikel bewerten und bei der Abstimmung einen Preis gewinnen – Details dazu gibt es hier. Eine Übersicht über alle am Bewerb teilnehmenden Artikel gibt es hier. Informationen zu den Autoren der Wettbewerbsartikel finden sich in den jeweiligen Texten.
Dieser Artikel ist Teil des ScienceBlogs Blog-Schreibwettbewerb 2017. Informationen zum Ablauf gibt es hier. Leserinnen und Leser können die Artikel bewerten und bei der Abstimmung einen Preis gewinnen – Details dazu gibt es hier. Eine Übersicht über alle am Bewerb teilnehmenden Artikel gibt es hier. Informationen zu den Autoren der Wettbewerbsartikel finden sich in den jeweiligen Texten.
——————————————————————————————————————
Umformen – quick and dirty
von Benjamin Remmers
Ich bin Maschinenbaumechanikergeselle und -ingenieur, wissenschaftlicher Mitarbeiter, Familienvater, podcastabhängig.
In einem Laborpraktikum im ersten Semester des Maschinenbaustudiums führe ich mit Studierenden einen Laborversuch an einer Reibradspindelpresse durch. Da die Studierenden zu diesem Zeitpunkt noch keine einschlägigen Vorlesungen gehört haben, muss ich auf die Schnelle die benötigte Formel herleiten und dabei die Grundlagen anreißen. Die wissenschaftliche Tiefe bleibt dabei natürlich ein wenig auf der Strecke, daher: quick and dirty und mit viel Augenzwinkern.
Im diesem Laborversuch soll aus der Formänderung einer Probe das Arbeitsvermögen einer Reibradspindelpresse bestimmt werden. Dieses Vorgehen kann man z. B. bei einer Maschinenprüfung im Rahmen einer regelmäßigen Wartung benutzen.
Eine Reibradspindelpresse ist eine sogenannte arbeitsgebundene Maschine. Das bedeutet in diesem Fall, dass das Arbeitsvermögen in Form von Bewegungsenergie vorliegt. Bei einem Umformprozess wird nun der Hauptteil dieser kinetischen Energie in die Umformung gesteckt und damit letztendlich in Wärme umgewandelt. Warum? Unsere Probe, ein Zylinder aus einer Aluminiumlegierung (AlMg3 H22), ist aus Kristalliten aufgebaut. Wenn jetzt auf die Kristallite eine Kraft wirkt, können die Atome im Gitter entlang der Gleitebenen gegeneinander verschoben werden, dabei entsteht Reibung und dabei entsteht Wärme. Auch durch die Messung der Wärmemengen-Änderung könnte man die Umformarbeit bestimmen. Doch ich schweife ab…
Je mehr Energie zur Verfügung steht, desto stärker wird sich die Probe umformen. Doch was heißt eigentlich „umformen“? Für uns Produktionstechniker heißt „umformen“, dass sich bei einem Werkstück die äußere Form ändert, ohne dass sich gewollt andere Eigenschaften verändern (auch wenn das praktisch natürlich anders ist). Im Speziellen spricht man von Volumenkonstanz (auch wenn Massenkonstanz eigentlich richtiger wäre). Drücke ich nun bei unserer zylindrischen Probe von den Stirnseiten aus auf die Probe, wird sie flacher und damit auch breiter. Wenn ich nun über die Umformung die Arbeit bestimmen möchte, brauche ich zunächst einmal eine Größe, mit der ich die Umformung darstellen kann.
Das erste, was den meisten Leuten einfällt, ist die Höhendifferenz, also
Der geneigte Leser fragt sich nun: Benötige ich für die Verkürzung einer Probe von 20mm auf 10mm die gleiche Energie wie für die Umformung einer 1000mm-Stange auf 990mm?
Vom Bauchgefühl her scheint diese Lösung unbefriedigend. Was soll man also tun? Man versucht es mit der Punktrechnung. Man könnte ja ein Verhältnis bilden und die Ausgangslänge miteinbeziehen:
Diese Formel definiert die Dehnung. Sie findet sich prominent in einem der Diagramme, ohne die man nicht Maschinenbau studieren kann, dem Spannungs-Dehnungs-Diagramm:

Dieses Diagramm ist werkstoffspezifisch und stammt aus dem Zugversuch. In diesem Versuch aus der Werkstoffkunde wird eine Probe mit bekanntem Querschnitt an ihren Enden in eine Zug-Prüfmaschine eingespannt und in die Länge gezogen. Dabei werden die Längenänderung und die wirkende Zugkraft gemessen. Die in der Probe herrschende Spannung wird berechnet, indem man die momentane Kraft durch die Querschnittsfläche teilt.
Beginnt man zu ziehen, befindet man sich zunächst im linken Bereich auf der Hookeschen Geraden. Hier ist die Formänderung elastisch, d.h. noch ist keine bleibende Umformung passiert. Wer schon einmal mit einer Büroklammer gespielt hat, kennt das als Rückfedern. Zieht man weiter, passiert häufig etwas Seltsames: Die Gerade knickt ab und beginnt zu flattern. Dies ist die ausgeprägte Streckgrenze. Danach beginnt nun die plastische Formänderung, es gibt also kein Zurück mehr in den Ausgangszustand. Dass die benötigte Kraft jetzt noch weiter ansteigt, liegt an der Kaltverfestigung. Diesen Effekt kennt man ebenfalls von der Büroklammer: Versucht man den Knick von eben wieder wegzubekommen, stellt man fest, dass der Draht sich lieber neben der eben gebogenen Stelle biegen möchte. Das liegt daran, dass der Werkstoff fester wird, je weiter ich ihn umforme (Versetzungen, die sich behindern und so).
Aber irgendwann werden die Spannungen in der Zugprobe wieder weniger. Wer lügt denn nun: Ich mit der Kaltverfestigung oder das Diagramm?
Das Diagramm lügt. Ab dem Spannungsmaximum beginnt sich die Probe einzuschnüren (wir erinnern uns an die Volumenkonstanz). Da für die Bestimmung der Spannung aber munter weiterhin durch den Ausgangsquerschnitt der Probe geteilt wird, entspricht die dargestellte (Ingenieurs-)Spannung gar nicht mehr der wahren Spannung.
Für unseren Versuch scheint das Spannungs-Dehnungs-Diagramm also aus zwei Gründen nicht geeignet zu sein: Erstens interessiert uns Umformer die elastische Formänderung nicht und zweitens stimmt die Kurve im relevanten Bereich nicht.
Und auch die Dehnung als Kennwert für die Umformung ist anzuzweifeln. Stellen wir uns eine Probe von 100mm Länge vor, die wir um 10mm zusammendrücken, so bekommen wir eine Dehnung von 10%. Machen wir die Umformung durch Ziehen wieder Rückgängig, erhalten wir eine Dehnung von 11%. Und eine Kenngröße, die für Hin- und Rückweg unterschiedliche Beträge annimmt, können wir hier nicht gebrauchen.
Was tut der geneigte Wissenschaftler, wenn die Punktrechnung versagt? Er logarithmiert.
Dies ist der Umformgrad. Für ihn bekommen wir bei dem Beispiel für Hin- und Rückweg denselben Betrag nur mit unterschiedlichen Vorzeichen (die verraten uns dann, ob gerade eine Dehnung oder eine Stauchung vorliegt). Passt.
Das für uns interessante Diagramm ist die Fließkurve. Sie ist die bildliche Darstellung der Kaltverfestigung. Auf der x-Achse ist der Umformgrad, auf der y-Achse die Formänderungsfestigkeit (die wahre Spannung) aufgetragen. Je weiter man umformt, desto fester wird der Werkstoff.
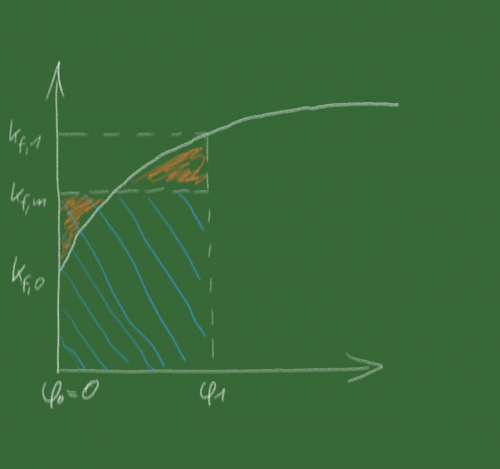
Das, was wir nun zur Berechnung der Umformarbeit benötigen, findet sich wie so oft in der Fläche unter der Kurve. Mathematisch gesprochen ist es das Integral der Fließkurvenfunktion in den Grenzen vom Zustand vor der Umformung (0) bis zum Zustand nach der Umformung (1). Aus dem Zugversuch fällt aber nur das Diagramm heraus. Und abgesehen davon ist das Integrieren sowas von oldschool. Und wir Fertigungstechniker sind normalerweise eher pragmatisch.
Man könnte jetzt das Diagramm in ein doppelt-logarithmisches Koordinatensystem eintragen und von der dann entstandenen Geraden einen Stützpunkt und die Steigung bestimmen…
Oder wir erlauben uns eine kleine Annäherung: Schaut man sich die Kurve an, stellt man fest, dass man die unregelmäßige Fläche auch durch ein Rechteck ersetzen kann, wenn man die mittlere Fließspannung verwendet und dann das Flächenstück über der oberen Seite benutzt, um die Lücke unter der Seite zu füllen. Eine Rechteckfläche lässt sich sehr leicht berechnen. HAbe ich schon erwähnt, dass Fertigungstechniker eher faul pragmatisch sind?
Jetzt brauchen wir für die Formel der Umformarbeit nur noch die Erkenntnis, dass wir mehr Arbeit benötigen, je mehr Material wir umformen. Da es ja die Grundregel der Volumenkonstanz gibt, bietet sich dafür das Zylindervolumen an.
Die Formel für die theoretische Umformarbeit ergibt sich nun zu:
Die Rechteckfläche aus der Fließkurve multipliziert mit dem Volumen der Probe.
Ich hoffe, ich konnte Euch einen kleinen Einblick in die Theorie der Umformtechnik bieten. Denkt daran, wenn Ihr das nächste Mal eine Münze, eine Getränkedose oder eine Autotür in der Hand habt, denn alle diese Teile sind mittels Umformverfahren hergestellt und vorher so oder so ähnlich (z. B. FEM basiert auf diesen Diagrammen und Formeln) berechnet worden.
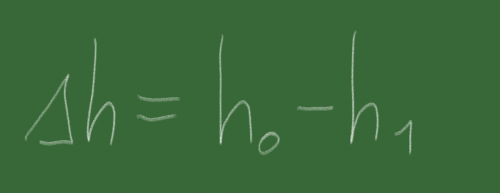
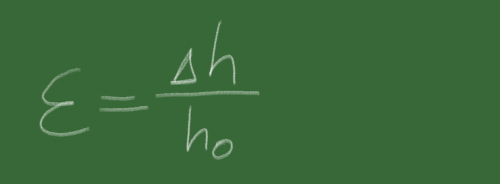
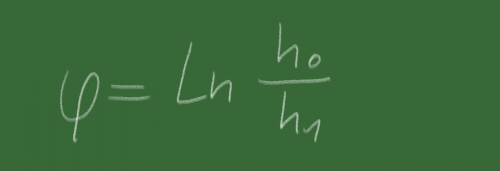
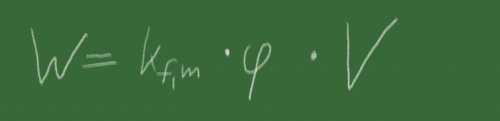
[…] am 12.10.2017: Link zum Artikel […]
Speziell – und ich habe längst nicht alles verstanden :-). Aber interessanter Einblick. Und zumindest Büroklammern werde ich jetzt mit anderen Augen sehen.
mein maschinenbaustudium ist schon ein weilchen her,
ja auch ich habe diese kurfen öfters im studium gesehen.
danach….? kann mich nicht erinnern diese jemals wieder gebraucht zu haben –
war aber auch kein ‚umformer‘.
aber das grosse „W“, ja, ohne dass ging es nie.
ein kleines thema, bunt angemalt – ja, so gehts auch: schön
…. hätt ich mal deutsch studiert
dann könnte in in kurven schreiben ….
oh, wie kann man hier mal was korrigieren?
Danke für die ersten Rückmeldungen!
Jetzt so online fällt mir auf, dass ein Bild der Maschine und der Proben hilfreich gewesen wären. Das liefere ich hier nach:
Reibspindelpresse
Probe vor und nach der Umformung
Immer dieses theoretisieren.
Einfach draufhauen.
Mein alter Meister, der mir vor Urzeiten die einfachen Grundlagen des Schmiedens beigebogen hat, kannte solce Formen sicher nicht. Hämmer, Zangen und ein gutes Feuer und es hat (bei ihm) immer millimetergenau gepasst.
Da hab ich auch gelernt , woher das Wort „Nägeln mit Köpfen machen“ herkommt. Nicht gar so leicht…
😉
Formeln, nicht Formen.
Nicht schecht,
für alle, die beim Lesen bereit sind mitzudenken.
Aber (und das ist nur ne Anregung und keine Kritik)
hätte ich einige Details gern etwas besser erklärt gehabt. So ist mir der Übergang bzw Unterschied zwischen elastischer und plastischer Verformung nicht klar genug geworden.
Die Idee mit den Tafelbildern finde ich sehr gut.
Hier wäre zur Pointierung auch eine Formel ala
σ =F/A
anschaulicher gewesen.
k,f ist leider gar nicht weiter erklärt.
Interessant ist der Trick die zu verrichtende Arbeit mit dem ϕ zu erklären. Verformung hin 10% ,zurück 11%. Kannte ich bisher noch nicht. Ich hätte es auch sehr anschaulich gefunden, den Grund für die logarithmische Abhängigkeit auf die Konstanz des Volumens (nicht der Masse) zu schieben. Wie am später eingefügten Bild sehr schön zu sehen ist, wird der Zylinderblock beim Pressen immer platter, aber dafür auch breiter. Das heißt: Der Block wird kürzer aber seine Oberfläche größer. Damit ändert sich auch was an der Spannung σ.
A*h = V=const
Man könnte das bei der Berechnung der Arbeit benutzen, aber dann müsste man wieder oldschool intergrieren können.
@ Pilot P
Von Interesse beim Umformen durch Stauchen beim Schmieden wären vielleicht noch die unterschiedlichen Querschnitts-Ausformungen der Proben.
Hier ab Seite 6 in idealisierter Form erwähnt:
https://books.google.at/books?id=76-hBgAAQBAJ&printsec=frontcover&dq=Freiformschmiede:+Erster+Teil&hl=de&sa=X&ved=0ahUKEwiK0P6r5evWAhWHthQKHfIbAwgQ6AEIJjAA#v=onepage&q&f=false
Flott und spaßig geschrieben!! Mehr davon…
@Pilot Pirx: Der gute, alte Meister macht halt vieles mit Erfahrung. Abgesehen davon ist Schmieden in den meisten Fällen Warmumformung, da gilt vieles von dem, was ich hier beschrieben habe, nicht. Bei einer Treibarbeit (kalt schmieden) ärgert man sich schon, wenn kurz vor der Fertigstellung Risse auftauchen, weil man den zulässigen Umformgrad überschritten hat.
@Fluffikowski: Danke für die Anregungen. Im Labor behandele ich das Thema mit Studierenden, die seit 4 Wochen Maschinenbau studieren. Da kann ich nur anreißen, was in den Vorlesungen Werkstoffkunde, Konstruktion und Fertigungstechnik in den nächsten beiden Semestern in der Tiefe gelehrt wird. Ich habe in der ganzen Veranstaltung auch nur 1,5h Zeit und möchte mehr praktisch an der Maschine arbeiten und auswerten.
Zur Spannung: Da wir mit einer arbeitsgebundenen Maschine arbeiten, (achtung, wieder leger formuliert) erhöht sich durch die Änderungen von Formänderungsfestigkeit und Querschnittsfläche ständig die Kraft.
@ImNetz: Interessanter Link. Massivumformung ist vom Prinzip her ja wirklich alt. Mit unseren Masterstudierenden halten wir jetzt allerdings einen Kurs „Trends in der Umformtechnik“ mit Dissertationen aus den letzten 5 Jahren.
Wer sich das ganze mal in natura ansehen möchte kann dies bei der Nacht des Wissens in Hamburg am 7.11.2017 gerne tun: Umformtechnik@HAW
@ B. Remmers
danke für den gut geschriebenen Blogbeitrag – gehört für mich natürlich zu den Besten – Ehrenwort!
Da das Problem des Umformen durch Stauchen von idealisierten kub. Körpern durch Pressen oder Schmieden vom wirtschaftlichen her zugunsten der Presstechnik ausgeht ist der uralte Artikel aus #9 eher ein Beispiel für die frühe erkannte Problemstellung.
Schade noch – aber leider liegt Hamburg gar arg weit weg von alpinem Gelände 😉
@Benjamin
Ich finde es sehr gut, dass du versuchst den neuen Studenten vor den Formeln ein praktisches Gefühl zu vermitteln.
Nur zum Verständnis:
Ich benötige also um 1000mm zu 990 mm umzuformen mehr Energie als 20mm zu 10mm zu formen.
Soweit richtig?
Es entsteht dabei auch mehr Wärme? Richtig?
Diese Versetzungen seien bei Wärme rückläufig. Wenn ich ein Werkstück so sehr presse, dass sehr viel Wärme und dann den Pressdruck entferne, geht das Werkstück wieder in seinen Ausgangszustand zurück?
@ anderer Michael:
Ich hoffe, ich bekomme das alles noch richtig zusammen. Umformtechnik ist schon etwas her.
Nein, entscheidend ist der Umformgrad für die benötigte Energie. Dein Beispiel kannst du ja auch so sehen, dass du 10 Stücke zu 100 mm um je 1 mm umformst. Du musst das große Teil relativ gesehen weniger umformen, daher weniger Energieeinsatz.
Das Volumen spielt eine kleinere Rolle.
Aber dabei entsteht Wärme.
Nein. Du muss immer unterscheiden, ob du elastische Verformung hast oder nicht.Solange du im elastischen Bereich bist geht die Verformung immer zurück. Sobald du aber mal den plastischen erreicht hast bleibt die Verformung. Durch Wärme kannst du zwar Gitterversetzungen beeinflussen, aber das ist auch wieder ein anderer Effekt. Zudem ändert sich mit steigender Temperatur der Bereich des Überganges elastisch-plastisch. Je höher die Temperatur desto eher kommst du in den plastischen Bereich. Und sobald du in dem bist gibt dir keine Temperatur wieder die Ursprungsform zurück. Aber genau das ist der Grund für das Schmieden: geringere Umformkräfte benötigt.
@ anderer Michael:
Erstmal ist die Frage, ob die Probe beim Stauchen von 1000mm auf 990mm eine andere Umformung erfährt, als beim Stauchen von 20mm auf 10mm.
Ich habe das für unsere Proben aber mal durchgerechnet:
1000mm auf 990mm:
V=706858mm³
φ=0,010
kfm=152,75N/mm²
W=1080Nm
20mm auf 10mm
V=14137mm³
φ=0,693
kfm=241,2N/mm²
W=2363Nm
Man benötigt für die kurze Probe also deutlich mehr Arbeit als für die lange, da der Umformgrad so viel größer ist. Und der geht ja zweimal ein: einmal direkt in der Fink’schen Gleichung und einmal in der Fließspannung.
Für die Warmumformung erwärme ich die Probe über die Rekristallisationstemperatur, d.h. die Kristallite bilden sich immer wieder neu und natürlich „verschwinden“ dabei auch die Versetzungen immer wieder, die ja hauptsächlich für die Kaltverfestigung und den maximalen Umformgrad verantwortlich sind.
Dafür bekomme ich Probleme mit Wärmeausdehnung/-schrumpfung und Zunderbildung. Bei der Halbwarmumformung versucht man die Vorteile aus beiden Verfahrensarten zu vereinen.
Benjamin
Ich habe null Ahnung von Technik und habe deinen Beitrag dreimal gelesen ( und nachgelesen) ,um überhaupt etwas zu verstehen.
Über die Formeln muss ich noch etwas nachdenken ( dauert bei mir immer länger).
Aber im Prinzip hast du ein Ziel in meinem Fall erreicht. Einen vollkommen Fachfremden für dein Thema interessiert und zum Denken motiviert . Deswegen sage ich „danke“, auch für die freundliche Antwort.
Dürfte ich noch eine Frage stellen?
Eine Autoteil einer Karosserie aus Stahl wird doch eingebaut , um dem Auto eine Festigkeit zu geben, die mit reinen Kunststoffteilen nicht erreicht wird ( außer wohl bei kleinen Autos, aber dort sind die Kunststoffteile sehr dick).
Wenn ich einen Kotflügel aus einer Stahlplatte umgangssprachlich presse (oder umforme) erreiche ich nicht nur die äußere Form, sondern durch die die Umformung und die kristallinen Veränderungen auf molekularer Ebene die gewünschte Steifigkeit für die Autokarrosserie, die bei der Ausgangsstahlplatte nicht gegeben ist ( wie ich beobachtet habe , wird diese manchmal in großen Rollen geliefert und ist wohl nicht sehr steif)?
Wenn dem so ist, dann kann man durch Veränderung des technischen Umformprozesses auch die gewünschte Steifigkeit erzielen und auch das Ausgangsmaterial danach abstimmen.?
Eine Coladose hat schließlich einen anderen Anspruch als ein Kotflügel.
Die Fragen sind bestimmt etwas albern. Aber ich wohne in einer Region , wo die Automobilzulieferindustrie einen bedeutenden Anteil der Wirtschaft hat und ich bekomme am Rande immer etwas davon mit.
Ich antworte jetzt mal nach Radio Eriwan: Im Prinzip ja!
Ich habe gerade keine Zeit, versuche aber spätestens morgen etwas dazu zu schreiben.
Funfact: Die Karosseriekonstrukteure würden gerne sehr hochfeste Stähle einsetzten, wo dann die Produktionstechniker sich fragen, wie sie die noch umformen sollen. Da gibt es dann Ansätze, wo die Halbzeuge entweder aus weicheren und steiferen Anteilen zusammengesetzt werden (tailored blanks) oder lokal zum Umformen erwärmt werden.
@ anderer Michael:
bin zwar nicht Benjamin, aber wenn er nichts dagegen hat kann ich dazu auch noch ein paar Infos geben:
Das mach man auch so.
Aber bei deinem Kotflügelbeispiel ist das nicht so einfach. Da wird ja nicht an jeder Stelle gleich umgeformt, und damit wird da auch nicht überall die gleiche Festigkeit durch das Umformen erzeugt.
Wo man das aber ganz gezielt einsetzt ist beim Herstellen zum Beispiel von Blechen, Rohren oder Profilen. Durch entsprechendes Auslegen von Umformprozessen und Wärmebehandlungen können gewünschte Festigkeiten eingestellt werden.
Und beim Auto gibt es noch andere Gründe für Stahl: Knautschzone.
Beim Umformen wird ja Energie verbraucht. Bei einem Unfall wird so dann ein Teil der Energie eines Aufpralls „verbraucht“, dadurch kommt beim Passagier weniger an. Deshalb will man auch keine extrem massive Karosserie, um eben auch durch das Umformen der Knautschzone die Passagiere zu schützen.
Kunststoff federt relativ stark oder bricht dann, da wird weniger Aufprallenergie durch Umformung umgewandelt. Da gab es irgendwann mal schöne Videos mit kleinen Autos, die wurden bei einem Aufprall mit geringer Geschwindigkeit komplett etwas zurückgeschleudert. Da kommen größere Belastungen bei den Passagieren an als mit Knautschzone.
@Terri: Danke für die Schützenhilfe!
@anderer Michael: Als die Produktionstechnik stark angefangen hat, zu simulieren, hat man sicherlich wohlwollend in Kauf genommen, dass die Blechteile durch die Umformung fester werden. Aber zumindest bei den Sichtteilen gewinnt immer das Design. Und bei Blechteilen werden dann für die Steifigkeit des Gesamtgebildes eher Sicken eingebracht oder weitere Bleche hinterklebt oder geschweißt.
Okay
jetzt ist mir klar , warum Benzinkanister aus Eisen Vertiefungen haben. Es sind Sicken für die Steifigkeit.Ehrlicherweise habe ich mir noch nie Gedanken darüber gemacht und an die Knautschzone habe ich gar nicht gedacht.
Zumindestens konnte ich das neu erworbene Minidetailwissen gestern anwenden können.Eines der Kinder schreibt heute Physik und ich konnte das Hook‘ sche Gesetz aus dem Stegreif erläutern. Ein anderes Kind sollte zur Übung eine Bewerbung schreiben. Ich half etwas beim Inhalt. So Begriffe wie Umformung und Reibradspindelpresse werden den Deutschlehrer hoffentlich von den Rechtschreibfehlern ablenken.
Jetzt schweige ich lieber.Ich habe einfach zu wenig Ahnung von der Materie und möchte nicht wie ein Troll mich benehmen.
Danke für die Antworten.
Ich sage meinen Studierenden immer, dass ich nur das erzähle, was ich interessant finde. Wenn sie allerdings danach fragen, was sie interessiert, dann kann ich ihnen auch das erzählen, und alle haben mehr Spaß. Also gerne weiter so.
Das mit den Sicken hat übrigens mit dem Biegemoment zu tun. Bei der Steifigkeit gegen Biegen gehen die Anteile der Querschnittsfläche stärker ein, die weit weg von der Mitte sind. Daher der Doppel-T-Träger (I-Profil). Bei dem braucht man den mittleren, senkrechten Streifen eigentlich nur, um die beiden horizontalen Bänder auf Abstand zu halten.
Die Sicke macht sozusagen das Blech an der betreffenden Stelle „dicker“.
Link vergessen: https://de.wikipedia.org/wiki/Profilstahl
Ich bin blöd.Vor Jahren haben meine Frau und ich einen Überstand vor dem Kellereingang gebaut.Als Dach (ungefähr 9 qm) nahmen wir Trapezbleche wegen der geringen Neigung.Die gesamte Konstruktion ist überdimensioniert was die Tragkraft betrifft, sowohl die Holzständer (Dicke und Abstand), als auch das Trapezblech.Weil ich die wenigen Informationen zum Bau nicht verstanden habe, habe ich vergleichbare Werke genommen und noch etwas aus Sicherheitsgründen draufgelegt( Also wenn der Ständer 6 x8 cm war , habe ich 7 x10 cm genommen) Das Ding kann wahrscheinlich 2 oder 3 m Pappschnee tragen.
Ich erinnere mich jetzt , es war beim Hersteller immer die Rede von Hoch- und Tiefsicken , als es um den Ort der Verschraubungen ging.Ich dachte , ich habe mich verhört, die meinen Senken.
Ist halb so schlimm, da wir es selber gemacht haben, war der Mehrpreis nicht so dramatisch.Das Dach ist dicht und die Kellerwand dort nun trocken
Bei Wikipedia ist ein Beispiel für ein 1mm Blech.Durch Sicken kann man die Spannweite um das 11 fache erweitern , bei nur 54% Mehrverbrauch an Material.
Das ganze ist ein Riesenthema, Balkentheorie usw ( habe dazu jetzt etwas gelesen und gehört eigentlich nicht zum Thema)
😉
@ anderer Michael:
Übrigens, bei Wellpappe nutzt man genau den gleichen Effekt.
Durch das Wellenprofil der mittleren Schicht wird das ganze senkrecht zu den Wellen unglaublich Steif, man benötigt aber weniger Material als bei einer Ganz dicken Pappe. Gewichtersparnis.
Und dein Trapezblech ist im Prinzip genau das gleiche.
Aus der Historie: Die Tante Ju (Flugzeug) war eines der ersten Flugzeuge mit vollständiger Metallbauweise, also nicht mehr Holz mit Stoff bespannt. Nur durch das Wellblech ging das, sonst wäre es zu schwer gewesen.
Ich gebe zu, als Ingenieur bin ich da vorbelastet, aber ein Total interessantes Thema in meinen Augen.