Erkenntnis durch Unwissenheit

Hinweis: Dieser Artikel ist ein Beitrag zum ScienceBlogs Blog-Schreibwettbewerb 2016. Hinweise zum Ablauf des Bewerbs und wie ihr dabei Abstimmen könnt findet ihr hier.

Das sagt der Autor des Artikels, Joachim Ripken über sich:
Ich bin Astrophysiker. Ich studierte Physik an der Universität Hamburg und promovierte da auch. Nach einer Postdoc-Zeit in Stockholm arbeite ich aktuell am Max-Planck-Insitut für Sonnensystemforschung in Göttingen.

——————————————
Erkenntnis durch Unwissenheit

In der Science Fiction-Serie „Raumschiff Enterprise; das nächste Jahrhundert“ kommt in der zweiten Folge der zweiten Staffel folgender kurzer Dialog vor:

Riker: Aber dieses Loch hat eine Form, Data, es hat Höhe und Breite.
Data: Mmh vielleicht. Vielleicht auch nicht.
Picard: Das ist sicher keine wissenschaftliche Antwort, Commander.
Data: Captain, es gibt eine grundlegende und sehr wertvolle Aussage in der
Wissenschaft. Sie ist ein Zeichen von Weisheit und lautet: Ich weiß es nicht.
Ich kann nur sagen: Ich weiß nicht, was das ist, Sir.

Dieser letzte Satz vom Serien-Ancroiden Data ist zum einen die vornehme Form der Frotzelei: „Wenn Du keine Ahnung hast, einfach mal die Klappe halten“. Aber die Weisheit des Satzes geht noch viel weiter. Den Drehbuchautoren war wahrscheinlich nicht bewusst bzw. bekannt, dass einige wichtige Erkenntnisse der Physik darauf beruhen was wir nicht wissen, bzw. was wir nicht wissen können. Über eine sehr weit reichende physikalische Erkenntnis, die alleine der Satz: „Ich weiß es nicht“ bringt, will ich hier schreiben.

Das Pauli-Prinzip
Ende des 19. und Anfang des 20. Jahrhunderts entwickelten die damaligen Physiker die Quantenmechanik als Theorie zur Beschreibung des Mikrokosmos. Insbesondere auch die chemischen und physikalischen Eigenschaften von Atomen sollten sich durch diese Theorie folgern lassen. Es wurde entdeckt, dass die Elektronen eines Atoms in verschiedene sog. Orbitale aufgeteilt sind.

Aus dem Chemie-Unterricht erinnern Sie sich vielleicht noch an die Hund’schen Regeln, wie sich die Elektronen aus die verschiedenen Orbitale, die auch verschiedenen Energie-Niveaus entsprechen aufteilen. Der Zustand eines Elektrons kann dabei durch vier sog. Quantenzahlen benannt werden. Der Physiker Wolfgang Pauli postulierte, dass keine zwei Elektronen eines Atoms in allen vier Quantenzahlen übereinstimmen können.

Alleine dieses Postulat hat schon sehr weitreichende Folgen. Je nachdem, wie die Orbitale gefüllt sind, können Atome/Moleküle mit anderen Atomen/Molekülen Bindungen eingehen, oder sie können sich gegenseitig abstoßen. Die Tatsache, beispielsweise, dass wir auf einem Stuhl sitzen können und nicht einfach durchfallen, obwohl die Atome selbst fast nur aus leerem Raum bestehen, beruht darauf, dass Atome/Moleküle, die keine Bindungen eingehen, einander abstoßen, und das lässt sich u.a. mit diesem Postulat von Pauli beschreiben und verstehen. Wir sitzen quasi auf dem Pauli-Prinzip.

Das Prinzip lässt sich noch weiter verallgemeinern, und damit kommen wir wieder zur Antwort von Data. Machen wir dazu mal folgendes kleines Gedanken-Experiment. Mit einem Messgerät beobachten wir zu einem gewissen Zeitpunkt zwei Elektronen an den Positionen A und B. Ein paar Augenblicke später wiederholen wir die Messung und sehen wieder zwei Elektronen, dieses Mal an den Positionen C und D. Nun ist die Frage: „Ist das Elektron, was bei Messung 1 an Position A war, jetzt auf C, und das B-Elektron wanderte zu D, oder ist es umgekehrt, dass das A-Elektron zu Position D wanderte und das B-Elektron bei der zweiten Messung bei C auftauchte?“ Die Antwort: „Ich weiß es nicht.“ Bzw. sogar viel besser: „Das können wir prinzipiell nicht wissen.“

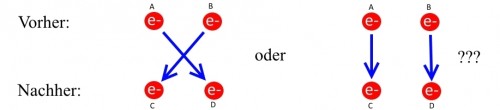
In der Quantenmechanik kann diese Antwort durchaus in die mathematische Beschreibung der Teilchen übersetzt werden. Die Teilchen werden dabei als sog. Wellenfunktionen beschrieben, und auch das gesamte Ensemble an Teilchen – in unserem Gedanken-Experiment zwei Elektronen – hat eine solche Wellenfunktion. Die Antwort „Ich weiß es nicht“ auf unsere Frage, bedeutet in die Mathematik der Quantenmechanik übersetzt: „Die physikalische Aussagekraft der Wellenfunktion darf sich nicht ändern, wenn wir zwei Teilchen darin vertauschen.“

Die Wellenfunktion besitzt auch eine Größe, die in der physikalischen Beobachtung keine Auswirkung hat: Die sog. Phase. Wir können also erlauben, dass sich die Phase der Gesamtwellenfunktion ändert, sollten wir zwei Teilchen darin vertauschen, aber die sonstige Form ändert sich nicht.

Wir unterscheiden nun zwei verschiedene Klassen von Teilchen. Bei sog. Fermionen ändert sich das Vorzeichen der Gesamtwellenfunktion, wenn wir zwei Teilchen vertauschen – der Wechsel des Vorzeichens ist eine spezielle Art des Phasenwechsels – bei den sog. Bosonen bleibt die Phase auch erhalten.

Spannend ist nun dieser Vorzeichenwechsel der Wellenfunktion bei Teilchenaustausch für die Fermionen. Wir erinnern uns: Die physikalische Aussage der Wellenfunktion darf sich nicht ändern. Das ist mathematisch nur möglich, wenn die Wellenfunktion für die Möglichkeit, dass beide Fermionen die gleichen Quantenzahlen haben, Null ist. Und das bedeutet schlicht übersetzt, dass keine zwei Fermionen der gleichen Art – also z.B. keine zwei Elektronen – in einem Atom die gleichen Quantenzahlen einnehmen können.

Chemische Bindungen und Nicht-Bindungen und das Verhalten fester Körper lassen sich quantenmechanisch herleiten, indem wir eine Frage mit „Ich weiß es nicht“ beantworten. Sie sehen, das ist eine äußerst wissenschaftliche Antwort, Captain Picard.