 Dieser Artikel ist Teil einer fortlaufenden Besprechung des Buchs „Wenn Gott würfelt: oder Wie der Zufall unser Leben bestimmt“ (im Original: „The Drunkard’s Walk: How Randomness Rules Our Lives“) von Leonard Mlodinow. Jeder Artikel dieser Serie beschäftigt sich mit einem anderen Kapitel des Buchs. Eine Übersicht über alle bisher erschienen Artikel findet man hier.
Dieser Artikel ist Teil einer fortlaufenden Besprechung des Buchs „Wenn Gott würfelt: oder Wie der Zufall unser Leben bestimmt“ (im Original: „The Drunkard’s Walk: How Randomness Rules Our Lives“) von Leonard Mlodinow. Jeder Artikel dieser Serie beschäftigt sich mit einem anderen Kapitel des Buchs. Eine Übersicht über alle bisher erschienen Artikel findet man hier.
——————————————————-
Im ersten Kapitel des Buchs hat Mlodinow anschaulich dargelegt, wie sehr der Zufall unser Leben bestimmt und vor allem dort, wo wir nicht damit rechnen. Das zweite Kapitel hat sich mit den grundlegenden Regeln der Wahrscheinlichkeit beschäftigt. Im dritten Kapitel präsentiert Mlodinow das fiese Ziegenproblem, das unser Unverständnis der Wahrscheinlichkeit eindrucksvoll präsentiert. Das vierte Kapitel beschäftigt sich mit den Methoden zur Berechnung von Wahrscheinlichkeiten die vor allem Blaise Pascal im 17. Jahrhundert entwickelt hat. Das fünfte Kapitel beschäftigt sich mit der Frage, was Wahrscheinlichkeiten in der realen Welt eigentlich bedeuten. Kapitel 6 erklärt die verwirrende Bayesschen Wahrscheinlichkeiten die für unser Alltagsleben von großer Bedeutung sind.
In Kapitel 7 wechselt Leonard Mlodinow das Thema. Bis jetzt ging es immer um Wahrscheinlichkeitsrechnung. Nun taucht das erste Mal die Statistik auf. Die beiden Themen sind zwar verwandt, aber unterschiedlich. In der Wahrscheinlichkeitsrechnung kennt man die Wahrscheinlichkeiten, mit der bestimmte Ereignisse eintreten schon vorher und nutzt sie, um die Wahrscheinlichkeit für den Eintritt anderer Ereignisse zu berechnen. Aber in der Realität will man oft auch andere Probleme lösen. Zum Beispiel in der Wissenschaft: Da geht es meistens nicht darum, dass man den Wert einer bestimmten Messgröße kennt und die Wahrscheinlichkeit bestimmen will, mit der die Messungen diesen Wert erreichen. Da hat man jede Menge Messungen und will damit den konkreten Wert der Messgröße bestimmen. Und dafür braucht man die Statistik.
Man muss sich außerdem im klaren darüber sein, dass jede reale Messung ein zufälliges Element beinhaltet (und dabei rede ich jetzt nicht von der Quantenmechanik). Mlodinow bringt das Beispiel der Englischlehrerin seiner Tochter. Hausarbeiten werden dort auf einer Skala von 1 bis 100 beurteilt. Aber was bedeutet es wirklich, wenn eine Arbeit mit der Note „92“ beurteilt wird und wie unterscheidet sich diese Arbeit von einer mit der Note „93“? Kann ein Lehrer wirklich objektiv so feine Unterscheidungen treffen? Studien zeigen, dass das nicht der Fall ist.
Lässt man unterschiedliche Lehrer die gleichen Arbeiten nach den gleichen Kriterien beurteilen, kommen sie trotzdem selten zum gleichen Ergebnis. Es spielen eben zu viele zufällige Faktoren eine Rolle. Genau so wie bei anderen subjektiven Beurteilungen, zum Beispiel dem Geschmack von Wein. Auch hier zeigen Studien regelmäßig, dass auch Experten nicht in der Lage sind, konsistente Beurteilungen abzugeben. Zu viele zufällige und psychologische Faktoren spielen Rolle. Weine, von denen man erwartet dass sie gut schmecken, werden besser beurteilt als sie beurteilt werden wenn die Tester vorher der Meinung sind sie würden schlecht schmecken. Zwei identische Weißweine werden unterschiedlich beurteilt wenn einer davon mit einem geschmack- und geruchlosen Farbstoff rot gefärbt wird und selbst wenn es nur daraus geht aus drei Weinen die beiden herauszuschmecken die identisch sind, sind die Experten nicht in der Lage, das zuverlässig zu tun. Und das gilt natürlich nicht nur für Wein: In Tests scheitern die Menschen auch regelmäßig daran, Coca Cola von Pepsi Cola zu unterscheiden, selbst wenn sie davon überzeugt sind, die eine Marke zu mögen und die andere nicht.

Wenn also 15 Weinexperten einem Wein (auf einer Skala von 1 bis 100) die Noten 80, 81, 82, 87, 89, 89, 90, 90, 90, 91, 91, 94, 97, 99 und 100 geben: Was hat das dann zu bedeuten? Und wie unterscheidet sich so ein Urteil von 15 Experten die dem Wein alle eine Note von 90 Punkten geben? Berechnet man den Durchschnitt der Noten, erhält man jedesmal 90 Punkte. Aber ganz offensichtlich unterscheidet sich der eine Fall vom anderen. In der ersten Serie gibt es viel mehr Variation und die wird mit der Standardabweichung beschrieben. Sie beträgt in diesem Fall 6 Punkte und alles was man über diesen Wein sagen kann ist, dass er eine Note hat, die irgendwo zwischen 84 und 96 liegt.
Die Standardabweichung von Daten wird oft vernachlässigt und es wird ignoriert, dass Variationen einer Größe innerhalb der Standardabweichung keine Bedeutung haben. Wenn zum Beispiel bei einer Meinungsumfrage herauskommt, dass die Zustimmung zur Politik der SPD von 30 auf 34 Prozent gestiegen ist, dann wird das die SPD sicherlich freuen und vermutlich wird die PR-Abteilung entsprechende Pressemitteilungen verfassen die erklären, dass die Bevölkerung die Arbeit der Partei würdigt, man auf dem richtigen Weg ist, und so weiter. Aber solange man die Standardabweichung nicht kennt, macht das alles keinen Sinn. Sagen wir, sie beträgt bei dieser Umfrage 5 Prozent. Das bedeutet folgendes: Würde man die Umfrage unmittelbar wiederholen, dann kann der Zustimmungswert dieses Mal auch bei 29 Prozent landen weil die SPD-Anhänger gerade alle am Klo waren und nicht ans Telefon gegangen sind. Oder aber man kriegt einen Wert von 39 Prozent. Wenn sich eine Messgröße um 4% ändert, die Standardabweichung aber 5% beträgt, dann ist die Änderung ohne Bedeutung weil es sich genau so gut um eine zufällige Fluktuation handeln kann.
Bei jeder realen Messung macht man Fehler und die hängen normalerweise vom Zufall ab. Die ersten, die sich intensiv damit auseinandersetzen mussten, waren die Astronomen im 17. und 18. Jahrhundert. Ausgerüstet mit Newtons Gravitationstheorie wollten sie die Bewegung der Himmelskörper berechnen und mussten dazu die Daten von Beobachtungen auswerten. Was ein Astronom misst, hängt von dem Gerät ab, das er benutzt, von den Unruhen in der Luft, von den Temperaturschwankungen, der Adaption der Augen an die Dunkelheit, der Stimmung des Astronom und jeder Menge anderer zufälliger Faktoren. Die Messwerte waren also nie identisch sondern variierten um einen Wert herum. Die Frage war nun: Wie genau sind die Messfehler verteilt?
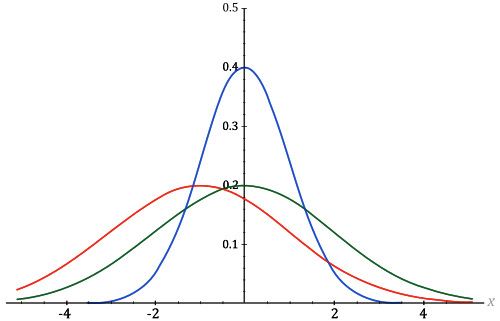
Das entsprechende mathematische Gesetz dass die Verteilung von Messfehlern bestimmt wird heute Normalverteilung oder Gaußverteilung genannt (nach Carl Friedrich Gauß, der es formuliert hat – obwohl vor ihm auch andere Wissenschaftler schon ähnliche Ideen hatten). Der Form der Verteilung nach wird sie auch „Glockenkurve“ genannt:
Wiederholt man eine Messung immer wieder und erstellt ein Diagramm, das anzeigt wie oft man einen bestimmten Wert erhalten hat, dann bekommt eine Kurve, die so aussieht wie in obigem Bild. Die meisten Messungen werden sich um einen Maximalwert herum verteilen; man wird aber auch immer wieder vereinzelte Messungen erhalten, die stark von diesem Wert abweichen. Die Kurve kann breit sein oder schmal und natürlich wird der Maximalwert je nach Art des gemessenen Phänomens ein anderer sein. Aber die grundlegende Form ist immer gleich und sie kann immer mit der gleichen mathematischen Formel beschrieben werden.
Diese Formel erklärt auch, wie die Standardabweichung zu interpretieren ist: Je stärker die einzelnen Messwerte varieren, desto breiter ist die Kurve. Folgen Messwerte einer Gaußverteilung, dann werden immer 68,27% der Messungen in einem Bereich von genau einer Standardabweichung landen. Würde man zum Beispiel 10.000 Weinexperten einen Wein testen lassen und ihre Noten aufzeichnen, würde man eine Glockenkurve erhalten. Sagen wir, der Maximalwert der Kurve liegt bei 56 Punkten und die Standardabweichung beträgt 5 Punkte. Dann haben 6827 Tester dem Wein eine Note gegeben, die zwischen 51 und 61 Punkten beträgt. 95,45% der Messungen liegen bei einer Glockenkurve im Bereich von zwei Standardabweichung. 9545 der Tester haben den Wein also mit einer Note zwischen 46 und 66 Punkten bewertet. 99,73 der Datenpunkte liegen im Bereich von drei Standardabweichung: 9973 Tester haben dem Wein zwischen 41 und 71 Punkte gegeben. Und so weiter.
Die Gaußverteilung erlaubt es, genau diese Zusammenhänge exakt zu berechnen. Führt man ein Experiment wiederholt durch, dann werden die zufälligen Fehler dafür sorgen, dass sich die Ergebnisse nach der Glockenkurve verteilen (das gilt aber nicht für systematische Fehler!). Eine genau Analyse ermöglicht es dann herauszufinden, wie exakt man mit diesen Messungen den tatsächlichen Wert bestimmt hat. Sie sagt uns aber auch, dass wir sehr gut aufpassen müssen, wenn wir nur wenige oder gar nur einen Datenpunkt zur Verfügung haben. Denn die Glockenkurve hat links und rechts kein Ende. Es wird zwar immer unwahrscheinlicher, dass ein einzelner Messwert extrem stark vom Mittelwert abweicht. Aber es gibt diese Abweichungen und wenn man nur eine einzige Messung macht kann man nicht sicher sein, dass man nicht gerade zufällig einen Extremwert gemessen hat, der vom tatsächlich Wert vollkommen abweicht.
Und das gilt um so mehr, wenn die ganze Sache chaotisch wird. Aber das passiert erst im nächsten Kapitel.
Die Geschichte mit dem Cola-Test ist mir kürzlich auch mal passiert. Da gab es eine Person, die behauptet hat, sie könne verschiedene Colas voneinander im Geschmack unterscheiden. Sie konnte nicht. Ich habe der Person gesagt, dass das ja auch völlig schnuppe ist. Ich ziehe zwar auch Pepsi der Coca Cola vor, aber ich habe den Verdacht, das liegt bei mir weniger am Geschmack. In Wirklichkeit gefallen mir wahrscheinlich die blauen Flaschen von Pepsi besser. Deshalb lasse ich mich da auch nicht auf Wetten ein. Ich könnte einen Unterschied ziemlich den Marken wahrscheinlich nicht schmecken.
Schönes 2014 erstmal, gute Gesundheit dir und den Menschen die du liebst!
Hab da eine Frage an dich:
du stellst ein fremdes Buch sehr ausführlich vor bzw. zur Diskussion, im Gegensatz zu deinem Eigenen.
Warum?
Ich fände eine Zusammenfassung von „Der Komet im Cocktailglas“, mit weiterführenden Links, lesenswert.
Vor allem die Meinungen deiner Leser zu den einzelnen Kapiteln wären sicher spannend!
@Geislwind: naja wenn ich meine Bücher so ausführlich vorstellen würde dann würde das sicher wieder als aufdringliche Werbung ausgelegt werden… Aber vielleicht mach ich später mal irgendeine zweitverwerwertung, mal sehen. Und ich finde es auch interessant über Bücher zu schreiben die andere Themen behandeln als die die ich sonst so im Blog behandle.
@ # 2
volle Zustimmung sowohl 2014 als auch Buch !
Ich habe eine Frage zur Normalverteilung: Mir ist klar, welche Folgerungen man ziehen kann, falls es sich um eine Normalverteilung handelt – wie aber kann man sich bei einer bestimmten Fragestellung sicher sein, dass sich die Messwerte wirklich gemäß einer Normalverteilung verhalten? Natürlich kann man viele Messungen durchführen und dann mit ziemlicher Sicherheit schätzen, dass es wohl eine Normalverteilung ist, aber eigentlich ist doch diese Aussage dann auch selbst schon wieder eine statistische/fehlerbehaftete, oder? Was, wenn es in Wahrheit eben doch keine Normalverteilung ist, sondern nur „ungefähr“?
@wrdlbrmpft
siehe bspw. https://de.wikipedia.org/wiki/Chi-Quadrat-Test
Dazu gibt es Testverfahren, die eben Wahrscheinlichkeiten ausspucken, dass die Messwerte tatsächlich zufällig variieren.
Aber auch das spuckt eben nur Wahrscheinlichkeiten aus.
[…] meiner Serie über Zufall und Wahrscheinlichkeit ging es heute um den Unterschied zwischen Statistik und Wahrscheinlichkeitsrechnung. Und passend dazu haben ein paar Schülerinnen ein sehr nettes Lied über Statistik […]
@wrdlbrmpft
Das war die Errungenschaft von Gauss: er hat mathematisch bewiesen, dass prinzipiell jeder Messwert, der von vielen unabhängigen Parametern beeinflusst wird, einer Normalveteilung folgt (genauer gesagt, die Verteilung nähert sich mit steigender Anzahl der Parameter einer Normalverteilung an) und zwar unabhängig davon, mit welcher Verteilung die einzelnen Parameter schwanken. Deshalb ist die Annahme, die Messwerte seien Normalverteilt so oft richtig. Es gibt natürlich Ausnahmen (z.B. radioaktiver Zerfall) und da versagt dann auch regelmäßig die normale Statistik.
@ StefanL, Daniel, Till:
Vielen Dank für die schnellen Reaktionen! Jetzt ist mir die Sache etwas klarer. Dennoch – ein Restrisiko bleibt wohl immer, dass man mit der Annahme der Normalverteilung falsch liegt. Aber vielleicht ist dieses Risiko auch meist vernachlässigbar klein gegenüber all den anderen Unsicherheiten, mit denen der Statistiker naturgemäß zu kämpfen hat…
@wrdlbrmpft
Die Normalverteilung folgt aus dem zentralen Grenzwertsatz. Wenn man ein Messergebnis aus der Summe zahlreicher unabhängiger Prozesse zusammengesetzt denkt, dann ergibt sich in Summe eine Normalverteilung.
@wrdlbrmpft
Stichwort „Zentraler Grenzwertsatz“
@ wrdlbrmpft
Stichwort „Zentraler Grenzwertsatz“
Die Gaußsche Normalverteilung ist jedeoch nur ein Spezialfall und trifft in der Realität oftmals nicht zu. Statistisch gesehen hat jeder Mensch ziemlich genau einen Hoden, aber die wenigsten Menschen haben genau einen. Da versagt der Gauß leider…….
Daher gibt es auch nicht „Das entsprechende mathematische Gesetz [sic] dass die Verteilung von Messfehlern bestimmt“, sondern es gibt unendlich viele, je nach Problemstellung.
Und die Begriffe „Wahrscheinlichkeitsrechnung“ und „Statistik“ differenzieren zu wollen, ist eh nur präskriptivistisch. Deskriptivistisch ergibt sich kein Unterschied. Soviel zur Linguistik.
Guten Tag , hab gerade gelesen das die welt am 22 .Februar untergehen soll stimmt das ?
@Marc: Nein.
Alles klar danke
Was sich aus solchen Wahrscheinlichkeitsverteilungen auch ergibt ist dass es häufig kein „Maximum“ oder „Minimum“ gibt, ab dem die Wahrscheinlichkeit =0 ist, bzw, dass die absoluten Extrema meistens relativ irrelevant sind.
Will ich zum Beispiel ein Zelt entwickeln, so muss dieses ja größer sein als die Leute die da rein sollen. Jetzt aber in einem Rekordbuch nach dem größten Menschen der Welt zu suchen ist aber unsinnig. Viel wichtiger ist der Punkt bei dem die Größe des Zeltes für, zum Beispiel, 90% der Bevölkerung ausreichend ist. Man spricht da auch vom 90-sten Percentil.
Wenn es erlaubt ist kommt #15 bis #17 in meine Sammlung seltsamer Dialoge …
..heißt „snippets-o-sthg.wri“, PDP10 – die extension müßte Dich ahnen lassen, in welch grauer Vorzeit das Sammeln begann.
Mach es heimlich, hat bei mir auch geklappt 😉
@PDP10, rolak:
#15 bis #17 dito. Endkrass.
@Andreas (Kommentar 1)
Klappt auch Prima mit Bier. Da kann man sogar nicht nur beobachten, dass Leute ihre Lieblingsbiersorte nicht erkennen und nicht besser finden als eine, die sie dem Vernehmen nach ablehnen. Man kann sogar sehr schon sehen, wie dieses objektive Faktum bei der weiteren Entscheidungsfindung gekonnt ausgeblendet wird (Confirmation Bias).
Ich habs dann lieber gleich so gemacht, dass ich erst empirisch meine Präferenzen ausgeleuchtet habe (5 Biere – 1 Abend, Messwiederholung am nächsten Abend) und habe dann erst meine Präferenzen getroffen.
(… Ich war „erschüttert“, dass es auch in Bayern gutes Schwarzbier gibt und nicht nur in Thüringen bzw. Tschechien, aber egal, an das Zeug aus Bayern komme ich nicht gut genug ran als dass es als Lieblingsbier taugen würde.)
ich bezweifle, das gott würfelt,
oder wie sagt A. Einstein:
der Alte würfelt nicht.
oder wie sagt W. Heisenberg:
Der erste Trunk aus dem Becher der Naturwissenschaft macht atheistisch, aber auf dem Grund des Bechers wartet Gott.
oder wie ich sage:
Zufälle gibt es nicht, das Universum bewegt sich, die Galaxien bewegen sich, die Erde dreht sich, und alles fügt sich zusammen.
Wenn man sich die Natur, die Erde, das Universum ansieht, so kann man wohl kaum von Zufall sprechen, ….
sondern man muss sich eingestehen, dass dahinter ein universale, kosmische intelligenz steckt, die ich, GOTT nenne, anderen nennen sie anders, jedoch sei es drum, Fakt ist, es ist Intelligenz gepaart mit Liebe.
#20 rolak
3. Januar 2014
Bin zwar nicht PDP10, tippe aber mal auf Wordpad unter Win95…
Kurze Recherche bei Wikipedia… – ups! Ziemlich weit daneben! Fehlerquelle war der Dateiname, der nicht ins 8.3-Raster passt, da Windows bis einschliesslich 3.11 ja noch ein reiner DOS-Aufsatz war und mit längeren Dateinamen nicht umgehen konnte.
Der Name hat sich auch zugegebenermaßen später verlängert, Hans, war schlicht ’snippets‘ bevor eine Erweiterung Richtung SOS möglich wurde.
Nein.
„sondern man muss sich eingestehen, dass dahinter ein universale, kosmische intelligenz [..], Fakt ist, es ist Intelligenz gepaart mit Liebe.“
Wie süss ….. aber ich stimme Dietmar zu …
Ähm … Nein.
@peacemaker:
Das Universum ist eine kalte, dunkle Maschine und interessiert sich einen Scheissdreck für dich …
@peacemaker
Einstein hat auch geschrieben:
“Was Sie über meine religiösen Überzeugungen gelesen haben, war natürlich eine Lüge, und zwar eine Lüge, die systematisch wiederholt wird. Ich glaube nicht an einen personalen Gott und habe das auch nie geleugnet, sondern es deutlich zum Ausdruck gebracht. Wenn etwas in mir ist, das als religiös bezeichnet werden kann, dann ist es die uneingeschränkte Bewunderung für die Struktur der Welt, soweit unsere Wissenschaft sie offenbaren kann.”
Letztendlich ist es aber wurscht, ob Einstein an einen Gott glaubte. Genauso wie es wurscht ist….
… was Heisenberg zum Gottesglauben schrieb. Oder dass die weit überwiegende Mehrzahl der Wissenschaftler nicht an einen Gott glaubt. Die Frage ist, ob es Belege für übernatürliches Wirken gibt. Und solche konnten bislang nicht ausgemacht werden.
Wir wissen viel mehr über die Entstehung des Universum, der Erde und der Natur, als du es anscheinend für möglich hältst. Und die Eingriffe eines übernatürlichen und allmächtigen Wesens sind dafür nicht notwendig.
Und das weißt du woher? Lass mich raten: Weil du es dir wünschst.
#25 rolak
Ah ja, interessant. – D.h. Du speicherst die immer noch als „write“-Datei?
Wenn nicht, auch egal. 😉
#28 Spritkopf
Auch wenn die Dauerleser / -kommentatoren es schon wissen, muss ich mich trotzdem mal wiederholen:
Es liegt in der Natur der Naturwissenschaften, dass sie die Existens einer Entität Namens GOTT mit ihren Methoden nicht beweisen können. D.h. sie können weder beweisen, das so etwas existiert, noch dass es nicht existiert. Und deshalb ist es jedem Menschen selbst überlassen, an die Aussagen der Religionen zu glauben oder es bleiben zu lassen. (freier Wille) Ebenso ist es allen Menschen selbst überlassen, aus der wundersamen Vielfalt und Komplexität der Natur dann metaphysische Schlüsse zu ziehen, wie den, dass da eine Schöpferkraft hinter stecken müsste. (Konjunktiv!)
Natürlich. Jeder Mensch kann Schlüsse ziehen wie er will. Allerdings gibt es keinen Grund, „aus der wundersamen Vielfalt und Komplexität der Natur“ „dann metaphysische Schlüsse zu ziehen“. Deswegen zieht sich die (gezähmte)Religion auch auf einen Gott der Lücken zurück. Menschen werden wohl immer eine Ecke finden, in denen sie einen irgendwie gearteten Gott platzieren können.
Vor 150 Jahren hat Jemand erkannt, dass es keiner „Schöpferkraft“ bedarf, sondern natürliche Prozesse ausreichen, all die Vielfalt zu erklären.
Ich finde, Darwin und Wallace haben die Menschheit mehr bereichert als ein (gutenteils erfundener) Christus.
@JolietJake
Ach ja, darüber kann man auch geteilter Ansicht sein. Allerdings hab ich auch was gegen den „Gott der Lücke“. Als ich beispielsweise das Buch von Anna Frebel gelesen habe, wo sie den Aufbau und die physikalischen Vorgänge der Sternenentstehung und wie es kommt, dass Sterne leuchten erklärt, da fand ich es einfach nur faszinierend, wie genial bzw. phantastisch der Herrgott (der Bibel) das alles geschaffen hat.
@Hans
Woher weißt du das? Wer hat dir dieses Wissen über diese Entität Gott vermittelt, dass dieser sich den Naturwissenschaften nicht zeigen würde? Die Bibel? Der Herr Pfarrer? Oder hat sich Gott dir persönlich offenbart? Und wenn ja, was hat er genau gesagt und woher weißt du, dass du nicht deiner eigenen Einbildung zum Opfer gefallen bist?
@Hans
Auch wenn die Dauerleser / -kommentatoren die Antwort schon kennen, muss ich dich trotzdem mal Fragen.
Kannst du oder irgendein Gläubiger Gott „beweisen“? . Wohl kaum, denn Phänomene die sich empirisch nicht prüfen lassen können wir höchstens glauben.
Gibt es irgendwelche Argumente die diese Existenz plausibel machen?
Und wie schaut es aus wenn ich jetzt behaupte, der Schöpfer sei ein unsichtbares Superwunderwarzenschwein, kannst du dann das Gegenteil „beweisen“?
Nein? Na dann ist es wohl auch jedem überlassen daran zu glauben oder es bleiben zu lassen. (freier Wille) Ebenso ist es allen Menschen selbst überlassen, aus der wundersamen Vielfalt und Komplexität der Natur dann metaphysische Schlüsse zu ziehen, wie den, dass da eine Schöpferkraft hinter stecken müsste. Oink!
@Hans
Aus deiner Aussage in #30 folgt dann stringent, dass Gott widernatürlich ist, ansonsten müssten die Naturwissenschaften ihn ja belegen können.
Ist es denn sinnvoll an etwas widernatürliches zu glauben und diesem widernatürlichen Etwas die Faszination der Wunder der Natur durch Schöpfung zuzuschreiben? Ich bin da etwas skeptisch.
Ansonsten wie üblich die Frage, die ma nan jeden Gläubigen richten muß, wie ist denn Gott definiert und wenn man eine Definition hat. warum ist es genau diese Definition von Gott, die richtig ist?
@Hans #30
Das Einstein-Zitat ist ja nur die Gegenthese zu peacemakers Einstein-Zitat über „den Alten“, das aussagen soll: sogar Einstein hat an Gott geglaubt, und dann muss es ihn ja auch geben.
Einstein hat jedenfalls nicht an einen persönlichen Gott geglaubt (diesen hat er mal als „childish“ bezeichnet) sondern fühlte sich eher dem Pantheismus à la Spinosa zugeneigt: die Natur an sich sei Gott. Damit der Pantheismus nicht atheistisch ist, muss man der Natur dann allerdings schon eine Zielgerichtetheit unterstellen, sonst belibt wenig Göttlichkeit übrig.
Für einen (Neu-)Amerikaner, der im öffentlichen Rampenlicht stand war es jedenfalls damals wie vielleicht auch heute noch gefährlich, sich als Atheisten zu outen, wenn man nicht bei Großteilen der Bevölkerung in Ungnade fallen wollte. Insofern mag Einstein sich mit seinem vorgeblichen Pantheismusbekenntnis einfach ein Hintertürchen offen gehalten haben, aber das ist Spekulation.
@Aldemarin
„Damit der Pantheismus nicht atheistisch ist, muss man der Natur dann allerdings schon eine Zielgerichtetheit unterstellen, sonst bleibt wenig Göttlichkeit übrig.“
In einem anderen Thread https://scienceblogs.de/astrodicticum-simplex/2013/04/18/ein-junger-nicht-beruhmter-physiker-denkt-uber-gott-nach/ #941, habe ich mal als Kompromiss zwischen Wissenschaft und Glaube vorgeschlagen, Gott=Natur (Pantheismus) und den Begriff Gott einfach nutzen, weil er sicher einen bestimmten Placeboeffekt für viele Menschen hat. Dieser Effekt besteht aber wohl nur, wenn man wie du treffend schreibst eine Zielgerichtetheit unterstellt. (Gebete erhören, beschützen etc.).
In dem genannten Kommentar #941hatte ich einiges vermischt oder unbewusst sogar ein wenig geschummelt.
Um ganz ehrlich zu sein, wenn die Dinge mal völlig schief laufen, bete ich auch mal ein wenig und stell mir im Grunde mehr oder weniger vor, der grosse allmächtige Papa beschützt mich. Obwohl mir bewusst ist was für ein Unsinn das ist, stelle ich fest, diese Gott/Pappa/allmächtiges Alphamännchen-Variante funktioniert bei mir am besten. Das ist dann aber kein Pantheismus mehr.
Am nächsten Tag habe ich keinerlei Probleme damit, zu behaupten, ich sei Atheist oder Pantheist. Widersprüchlich?
Erklärungsversuch:
Ist es nicht so, dass Placebos sogar wirken können obwohl man weiss, dass da eigentlich nichts ist was wirken kann und lässt sich das nicht auf meinen „Spagat“ übertragen oder bin ich jetzt ein Heuchler, kindlich naiv oder gar schizophren und sollte mich mal behandeln lassen.
Ängste und Sorgen können manchmal irrationale Formen annehmen und wenn die „Beruhigungspille“ funktioniert, ist das doch legitim, oder? Sozusagen ein bewusste, kurzzeitige Selbsttäuschung ohne negative Nebenwirkung. Natürlich vertraue ich nicht wirklich darauf, dass Gott mich schützt oder „die Natur auf meiner Seite ist“ und setze in der Realität im allgemeinen und besonders bei bestehenden Problemen, auf rationales Denken.
„Wenn sich eine Messgröße um 4% ändert, die Standardabweichung aber 5% beträgt, dann ist die Änderung ohne Bedeutung weil es sich genau so gut um eine zufällige Fluktuation handeln kann.“
Wenn es sich um Änderungen des Mittelwertes einer Meßgröße handelt, kann man das so nicht allgemein sagen. Bei großer Samplegröße sinkt der Standardfehler und die Trennschärfe steigt. Problematisch bleibt natürlich gerade bei Wahlumfragen immer der unbekannte systematische Fehler. Etwas Bias durch Stichprobenwahl und Einflüsse durch Medien etc.
@naseweis
Das wäre bereits ein „persönlicher Gott“, der Dir persönlich einen Gefallen tun soll. Mit „Zielgerichtetheit“ meinte ich eher, dass der pantheistische Gott bzw. die Natur das Universum so geformt hat, dass und damit wir dabei herausgekommen sind. Wenn man nicht mal dies der Natur unterstellt, dann verliert sich der Gottesbegriff in der Aussagenlosigkeit und man ist bereits Atheist, ohne es zuzugeben.
Dies zu empfinden ist völlig normal und vielleicht die grundlegende Ursache für Religiosität. Als Kinder haben wir große starke Eltern, die uns beschützen (jedenfalls ist dies das Grundgefühl eines Kindes). Die spielen irgendwann keine Rolle mehr, aber in Situationen der Hilflosigkeit ist die Sehnsucht nach den Beschützern wieder präsent. Die Religion bietet einen solchen Beschützer an, also wird er dankend angenommen. Der Rest ist dann Placebo, wie Du sagst.
Wenn’s einen tröstet, ist das auch ok. Gefährlich wird’s dann, wenn es das Handeln mehr lenkt als die Ratio, und wenn man sich daraus Rechte ableitet, über andere zu bestimmen. Ist wie der Unterschied zwischen einem Glas Wein und Alkoholsucht.
@Alderamin (diesmal richtig)
„Dies zu empfinden ist völlig normal und vielleicht die grundlegende Ursache für Religiosität.“
Das vermute ich auch.
„Ist wie der Unterschied zwischen einem Glas Wein und Alkoholsucht.“
Gut, damit kann ich leben.
@Alderamin
Da kann ich auch mitgehen.
Gut geschrieben.