Wie beschreibt man die Bahn eines Himmelskörpers?

Die Himmelsmechanik beschäftigt sich mit der Bewegung von Himmelskörpern (Sterne, Planeten, Asteroiden, Kometen, Monde, …). Dafür braucht man natürlich ein Koordinatensystem.

Wenn wir z.B. Objekte in unserem Sonnensystem betrachten, dann wäre die heliozentrischen Koordinaten die einfachste Wahl. Dabei verwendet man einfach ein „normales“ dreidimensionales kartesisches Koordinatensystem mit der Sonne im Ursprung. Ein Objekt, das sich um die Sonne bewegt hat dann 3 Ortskoordinaten (x,y,z) und drei Geschwindigkeitskoordinaten (vx, vy, vz) die angeben, wie schnell sich das Objekt in eine bestimmte Richtung bewegt. Durch diese 6 Koordinaten ist die Position eines Himmelskörpers eindeutig bestimmt.

Für bestimmte Anwendungen sind die heliozentrischen Koordinaten aber etwas unpraktisch. Was einen in der Himmelsmechanik oft interessiert, ist nicht die Bewegung eines Objekts an sich, sondern die Änderung der Bahn des Himmelskörpers. Laut Keplers ersten Gesetz bewegen sich Planeten und Asteroiden auf elliptischen Bahnen um die Sonne. Da nun aber nicht nur die Sonne eine gravitative Kraft auf die Planeten ausübt, sondern die Planeten sich auch untereinander beeinflussen, ändern sich diese Ellipsen aber im Laufe der Zeit!

Die Bahnellipsen der Planeten werden mit der Zeit normalerweise größer und kleiner, elliptischer und weniger elliptisch, sie drehen sich im Raum hin und her… Wenn sich die Planeten (oder Asteroiden, Kometen, …) auf stabilen Bahnen befinden, dann finden diese Schwankungen nur innerhalb gewisser Grenzen statt. Bei Objekten auf instabilen/chaotischen Bahnen, werden diese Schwankungen immer größer und größer bis der Himmelskörper in die Sonne stürzt, aus dem Sonnensystem fliegt oder mit einem anderen Objekt kollidiert. Um nun herauszufinden, ob sich Objekte auf stabilen oder instabilen Bahnen befinden, untersuchen Himmelsmechaniker deswegen nicht die Änderungen der heliozentrischen Koordinaten (x,y,z,vx,vy,vz) sondern die Änderungen der Bahnelemente.

Diese Bahnelemente sind ein Koordinatensystem, basierend auf den Eigenschaften der Bahn eines Himmelskörpers. Sie setzen sich aus 6 verschiedenen Größen zusammen:

• Die große Halbachse (a) der Bahn. Die Bahn eines Objekts um die Sonne wird durch eine Ellipse beschrieben. Die Form einer Ellipse ist definiert durch kleine Halbachse (grün) und große Halbachse (rot):

• Die Exzentrizität (e) der Bahnellipse. Je exzentrischer eine Ellipse ist, desto größer ist die Abweichung von der Form eines Kreises. Die Exzentrizität wird mit einer Zahl zwischen 0 und 1 angegeben. Ein Kreis hätte eine Exzentrizität von e=0; mit steigender Exzentrizität wird die Ellipse immer langestreckter bis schließlich bei e=1 die Ellipse zu einer Linie wird.

Große Halbachse und Exzentrizität definieren die Form der Ellipse. Diese Bahnellipse hat nun aber auch eine bestimmte Lage im dreidimensionalen Raum. Daher werden noch 3 weitere Parameter benötigt, um zu definieren, wie die die Ellipse im Raum orientiert ist:

• Die Inklination (i) der Bahn. Die Inklination bzw. Bahnneigung gibt an, wie stark die Bahnellipse gegenüber der Ekliptik geneigt ist. Die Ekliptik ist die Referenzebene im Sonnensystem und entspricht der (mittleren) Bahnebene der Erde. Eine Bahn mit z.B. einer Inklination von i=5° ist um 5° gegenüber der Erdbahn geneigt.

• Die Länge des aufsteigenden Knotens (Ω). Der Punkt, an dem die Bahn eines Himmelskörpers die Ekliptik von Norden nach Süden durchstößt, nennt man absteigender Knoten (☋). Der Punkt, an dem die Bahn die Ekliptik von Süden nach Norden durchstößt, nennt man aufsteigender Knoten (☊)¹. Der Winkel zwischen der Verbindungslinie Sonne-Aufsteigender Knoten und der Verbindungslinie Sonne-Frühlingspunkt ist die Länge des aufsteigenden Knotens. Der Frühlingspunkt (♈) ist ein fixer „Nullpunkt“ der als Bezugspunkt für astronomische Koordinaten dient. Es ist jener Punkt am Himmel, an dem die Sonne genau am astronomischen Frühlingsanfangt steht).

• Das Argument des Perihels (ω). Das Argument des Perihels ist der Winkel zwischen der Verbindungslinie Sonne-Perihel (der sonnennächste Punkt auf der Bahn) und der Verbindungslinie Sonne-aufsteigender Knoten.

Diese drei Parameter (i, Ω, ω) definieren die Lage der Ellipse im Raum. Die Bahnellipse des Himmelskörpers ist nun also durch große Halbachse, Exzentrizität, Inklination, Länge des aufsteigenden Knotens und Argument des Perihels eindeutig definiert. Es fehlt jetzt aber noch ein weiterer Parameter um die Position des Himmelskörpers auf dieser Bahn festzulegen. Dafür gibt es mehrere Möglichkeiten; die häufigste ist

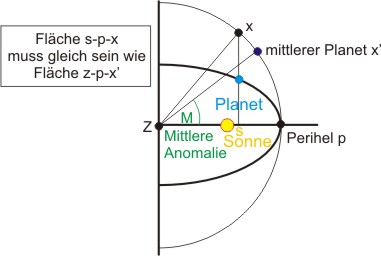
• Die mittlere Anomalie (M). Zur Definition der mittleren Anomalie geht man von einem „mittlerem Objekt“ aus, das die gleiche Umlaufzeit hat wie der echte Himmelskörper und auch zur gleichen Zeit das Perihel durchläuft. Dieses mittlere Objekt bewegt sich allerdings mit konstanter (Winkel)Geschwindigkeit auf einer Kreisbahn (mit einem Radius, der gleich der großen Halbachse des echten Objekts ist) um die Sonne. Der Winkel zwischen der Verbindungslinie Kreismittelpunkt-mittleres Objekt und der Verbindungslinie Kreismittelpunkt-Perihel ist die mittlere Anomalie.

  Sie lässt sich auch leicht mit folgender Formel berechnen:

  

  t₀ ist hier der Zeitpunkt des Periheldurchgangs und U die Umlaufperiode des Himmelskörpers.

Diese 6 Parameter (a, e, i, Ω, ω, M) sind die Bahnelemente! Mit ihnen läßt sich die Position und Geschwindigkeit eines Himmelskörpers genauso exakt beschreiben wie mit den heliozentrischen Koordinaten.

Will man nun wissen, wie sich die Bahn eines Himmelskörpers im Laufe der Zeit verändert, muss man untersuchen, wie sich die Bahnelemente im Lauf der Zeit ändern. Im folgenden Bild² sieht man beispielsweise, wie sich die Exzentrizitäten von Erde und Venus während eines Zeitraums von 5 Millionen Jahren ändern:

Hier sieht man was ich oben beschrieben habe: Die Exzentrizitäten werden periodisch größer und kleiner – aber die Änderungen finden nur innerhalb gewisser Grenzen statt: Die Bahnen von Erde und Venus sind stabil. Man sieht hier auch schön, dass die Bahnänderungen von Erde und Venus gekoppelt sind: immer dann, wenn die Exzentrizität der Erde größer wird, wird die der Venus kleiner (und umgekehrt).

Über Bahnelemente gäbe es noch viel mehr zu sagen – vor allem auch über die genauen Wege, wie man ihre Änderungen berechnet (und über die anderen Typen von Bahnelementen). Aber das würde jetzt zu weit führen…

Fussnoten:
¹ „Norden“ bezieht sich hier auf die Nordrichtung der Erdachse

² Das Bild stammt aus dem Buch: „Chaos and Stability in Planetary Systems“ (Rudolf Dvorak, Florian Freistetter, Jürgen Kurths), ISBN 978-3540282082

Dieser Artikel wurde schon früher in meinem alten Blog veröffentlicht. Da ich aber in nächster Zeit einige Beiträge schreiben möchte, für die die Bahnelemente wichtig sind, habe ich ihn hier nochmal eingestellt.