Neue Tricks für alte Teleskope: Hubble und die Entfernungsmessung

Man kann eigentlich nicht oft genug betonen, wie fundamental wichtig die Entfernungsmessung für die Astronomie ist. Das mag vielleicht seltsam erscheinen – wieso soll es so enorm wichtig sein zu wissen, wie weit weg so ein Stern oder so eine Galaxie ist? Aber man muss sich ja nur mal ansehen, wie der Stand der Dinge zu einer Zeit war, als man noch keine Ahnung hatte, wie weit die Sterne wirklich entfernt war. Damals war die Astronomie im wesentlichen nur himmlische Buchhaltung. Die Astronomen erstellten jede Menge Kataloge und maßen die Position und die Helligkeit der Sterne. Und recht viel mehr konnten sie auch nicht tun. Denn die Entfernung ist der Schlüssel zu allen weiteren Informationen. Will man wissen wie groß ein Stern ist; wie schwer, wie heiß, und so weiter: Dann muss man wissen, wie weit er entfernt ist. Von der Erde aus sind die Sterne nur Lichtpunkte am Himmel. Ein heller Lichtpunkt kann ein kleiner und naher Stern sein. Oder ein großer Stern, der weit weg ist. Ohne seine Entfernung zu kennen wissen wir nichts über seine intrinsischen Eigenschaften und ohne die ist es unmöglich, die Sterne selbst zu verstehen.

Ohne die Entfernungsmessung gibt es keine moderne Astrophysik. Ohne Entfernungsmessung verstehen wir die grundlegende Struktur der Milchstraße nicht. Wir verstehen die Entwicklung des Universums nicht. Wir verstehen eigentlich kaum irgendwas, wenn wir nicht wissen, wie weit die hellen Punkte am Himmel entfernt sind. Und es ist kein Wunder, dass die große Revolution in der Astronomie und Naturwissenschaft gerade Anfang des letzten Jahrhunderts begann, als es den Astronomen endlich gelang, die Entfernung nicht nur zu den allernächsten Sternen sondern auch zu den fernen Galaxien zu messen. Der Mann, der damals maßgeblich beteiligt war hieß Edwin Hubble und nach ihm wurde auch das Teleskop benannt, das die Entfernungsmessung kürzlich massiv verbessert hat.

Es gibt viele verschiedene Methoden der Entfernungsmessung (siehe hier und hier) und die meisten davon basieren auf diversen Schätzwerten. Aber eine Methode liefert wirklich genau und zuverlässige Entfernungswerte: Die Messung der astronomischen Parallaxe.

Das Prinzip dahinter ist simpel und jeder kann es leicht selbst ausprobieren: Steckt die Hand und euren Daumen aus. Betrachtet den Daumen zuerst nur mit dem rechten Auge; dann nur mit dem linken Auge. Wenn ihr zwischen den Augen hin und her wechselt, dann scheint auch euer Daumen vor dem Hintergrund hin und her zu springen. In Wahrheit tut er das natürlich nicht, sondern bleibt dort, wo er ist. Aber weil ihr ihn mit unterschiedlichen Augen aus leicht unterschiedlichen Blickwinkeln betrachtet, seht ihr ihn vor einem jeweils leicht unterschiedlichen Hintergrund. Je näher der Daumen euren Augen ist, desto stärker scheint er zu springen und ihr könnte seinen Abstand aus dem Ausmaß seiner scheinbaren Bewegung berechnen.

Genau so funktioniert es auch mit den Sternen. Hier nutzt man die Tatsache, dass sich die Erde selbst durch den Raum bewegt. Einmal im Jahr bewegt sie sich einmal um die Sonne herum. Sie bewegt sich auf einem annähernden Kreis mit einem Durchmesser von 300 Millionen Kilometer und beobachtet man den Sternenhimmel zum Beispiel mal im Januar und mal im Juli, dann liegen zwischen den Beobachtungspositionen genau diese 300 Millionen Kilometer. Man blickt also aus unterschiedlichen Winkeln auf die Sterne und so wie der Daumen sollten auch die sich leicht vor dem Hintergrund bewegen. Diese Bewegung nennt man „Parallaxe“ und dem Astronomen Friedrich Wilhelm Bessel gelang das erste Mal 1838 sie bei einem Stern zu messen.

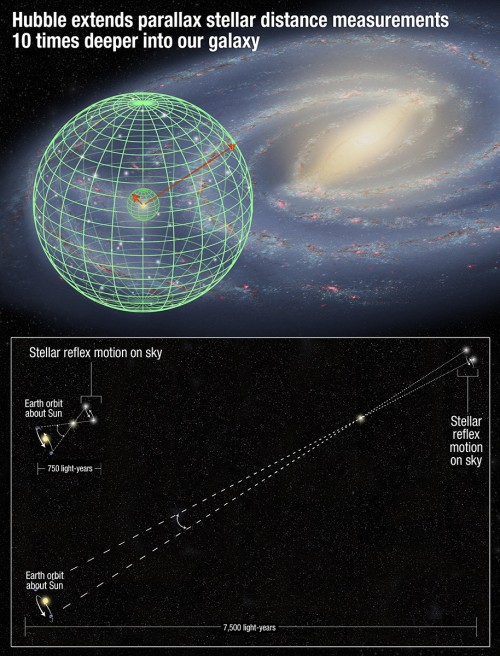
Das Problem ist, dass die Sterne eben verdammt weit weg sind und die Parallaxe dementsprechend klein. Man muss schon sehr genau messen, um die Positionsveränderung beobachten zu können. Selbst mit den modernen Teleskopen gelang das bisher nur bei Sternen in der unmittelbaren Nachbarschaft der Sonne, die höchstens ein paar hundert Lichtjahre weit weg waren. Für fernere Objekte musste man auf die ungenaueren anderen Methoden zurückgreifen. Aber nun hat das Hubble-Teleskop gezeigt, dass man auch 10 Mal weiter entfernte Sterne mit der Parallaxen-Methode genau vermessen kann.

Hubble ist zwar schon 24 Jahre alt, aber immer noch eines der wichtigsten Instrumente für die Astronomen. Adam Riess ist schon ein wenig älter, hat aber auch jede Menge Erfahrung mit der Entfernungsmessung. 1998 hat er den Abstand zu fernen Supernova-Explosionen bestimmt und im Zuge dessen die dunkle Energie entdeckt und dafür den Nobelpreis für Physik bekommen. Jetzt hat er sich eine neue Technik ausgedacht, um auch die Parallaxenmessung zu verbessern. Um die scheinbare Veränderung der Sternposition messen zu können, braucht man logischerweise möglichst scharfe Bilder. Riess dachte sich, dass man aber mal probieren könnte, keine punktförmigen Bilder der Sterne aufzunehmen, sondern sie durch das Bildfeld des Teleskops wandern zu lassen. Dann sieht man auf den Aufnahmen lange Sternspuren und Riess und seine Kollegen fanden ein paar neue mathematische Tricks, mit denen sich solche Strichdaten genauer und besser auswerten lassen als vorher die konventionellen Aufnahmen („Parallax Beyond a Kiloparsec from Spatially Scanning the Wide Field Camera 3 on the Hubble Space Telescope“).

Es gelang ihnen mit dieser neuen Methode, die Entfernung zu einem 7500 Lichtjahre entfernten Stern enorm genau zu messen; etwas, das bisher nur bis zu Entfernungen von knapp 750 Lichtjahren möglich war. Bevor demnächst die neuen und revolutionären Entfernungsmessungen des GAIA-Teleskops gemacht werden, hat das alte Hubble-Teleskop also noch mal gezeigt, dass es auch noch ein paar gute Daten liefern kann. Mit der Messung der Entfernung zu einem schnöden Stern in unserer Milchstraße macht man vielleicht keine große Schlagzeilen in den Medien. Aber man schafft die Voraussetzungen für große Entdeckungen in der Wissenschaft. Und darauf kommt es ja eigentlich an…