 Das ist die Transkription einer Folge meines Sternengeschichten-Podcasts. Die Folge gibt es auch als MP3-Download und YouTube-Video. Und den ganzen Podcast findet ihr auch bei Spotify.
Das ist die Transkription einer Folge meines Sternengeschichten-Podcasts. Die Folge gibt es auch als MP3-Download und YouTube-Video. Und den ganzen Podcast findet ihr auch bei Spotify.
Mehr Informationen: [Podcast-Feed][iTunes][Bitlove][Facebook] [Twitter]
Über Bewertungen und Kommentare freue ich mich auf allen Kanälen.
—————————————————
Sternengeschichten Folge 440: Die Gravitationskonstante
Ohne Gravitation geht nichts im Universum. Vor allem in der Astronomie, wo es ja meistens um sehr massereiche Objekte wie Sterne oder Planeten geht, kommt man ohne Gravitation nicht aus. Wenn man das Universum in seiner Gesamtheit verstehen will, braucht man die Gravitation. Man braucht sie auch, wenn man alles andere verstehen will – immerhin ist die Gravitation eine der vier fundamentalen Kräfte der Natur. Und wenn man wissen will, wie eine Kraft funktioniert, dann muss man natürlich auch wissen, wie stark sie ist.
Wir alle haben in der Schule von Newtons Gravitationsgesetz gehört. Im 17. Jahrhundert hat Isaac Newton festgestellt, dass die Gravitationskraft zwischen zwei Objekten proportional zu den Massen der beiden Objekte ist und indirekt proportional zum Quadrat ihres Abstandes. Aber wir wollen ja wissen, wie stark die Kraft genau ist. Das mit dem „proportional“ heißt in dem Fall ja nur: Wenn die Masse der Objekte größer wird, wird die Gravitationskraft im gleichen Ausmaß größer. Und wenn der Abstand größer wird, dann sinkt die Kraft und zwar nicht im gleichen Ausmaß, sondern schneller (weil sie ja zum Quadrat des Abstands proportional ist). Das zu wissen ist gut, wenn man prinzipiell verstehen will, wie die Gravitationskraft funktioniert. Aber wenn man konkret berechnen will, wie stark die Kraft ist – zum Beispiel weil man wissen will, wie sich die Himmelskörper bewegen und wohin sie sich bewegen – dann reicht das „proportional“ nicht. Deswegen findet man in Newtons Gravitationsgesetz auch noch eine Zahl, eine „Proportionalitätskonstante“. Die exakte Formel lautet: Gravitationskraft ist gleich Masse eins mal Masse zwei, geteilt durch den Abstand zum Quadrat und das ganze nochmal multipliziert mit G.
Womit wir jetzt beim Thema dieser Folge sind: G. Das ist die Gravitationskonstante. Es ist eine Naturkonstante und sie sagt uns, wie stark die Gravitationskraft ist. Ohne den genauen Zahlenwert von G zu kennen, können wir keine Gravitationskräfte zwischen Objekten berechnen. Das gilt übrigens nicht nur für die Formel von Isaac Newton. Seit 1915 haben wir ja eine neue, bessere Beschreibung der Gravitation von Albert Einstein, die allgemeine Relativitätstheorie. Und auch in diesen Formeln finden wir G. Was auch sonst; diese Zahl muss immer auftauchen, wenn es um Gravitation geht.
Aber schauen wir nochmal zurück ins 17. Jahrhundert, zu Isaac Newton. Als er damals seine Formel zur Gravitation aufgestellt hat, war ihm natürlich klar, dass er dafür die Zahl braucht, mit der man die Stärke der Gravitation angibt. Er konnte sie damals aber nicht bestimmen; es gab keine Messgeräte dafür und er konnte sie nur schätzen. Das reicht in der Wissenschaft aber nicht, wenn es um Naturkonstanten geht, dann wollen wir die so exakt wie nur irgendwie möglich kennen. Das ist aber – gerade bei der Gravitationskonstante enorm schwer.
Der offiziell zur Verwendung empfohlene Wert – und ja, es gibt natürlich eine internationale Organisation die dafür zuständig ist, die jeweils besten bekannten Werte physikalischer Konstanten zu sammeln und zu bewerten, das „Committee on Data for Science and Technology (CODATA)“ – dieser offizielle Wert für die Gravitationskonstante beträgt 6,67430 mal 10 hoch minus 11 Kubikmeter pro Kilogramm pro Sekunde zum Quadrat. Sicher ist man sich aber nur beim 6,674-Teil dieser Zahl, schon die nächsten Stellen sind nicht mehr genau, da könnte es auch mit 2 oder 4 weitergehen. Und das ist schon ein wenig unangenehm. Wenn man sich die anderen Naturkonstanten anschaut – den Wert der Lichtgeschwindigkeit, die Masse eines Elektrons, das Plancksche Wirkungsquantum, und so weiter – dann kennen wir sie entweder exakt oder zumindest sehr, sehr, sehr genau. Nur bei der Gravitation kriegen wir immer noch nicht mehr als zwei, drei sichere Stellen hinter dem Komma hin.
Das liegt natürlich einerseits daran, dass die Gravitation eine enorm schwache Kraft ist. Das klingt ein wenig widersprüchlich – ist es aber gar nicht. Ich kann problemlos ein bis zwei Meter hoch in die Luft springen (je nach körperlicher Leistungsfähigkeit), obwohl die GESAMTE ERDE mit der Gravitationskraft ihrer Masse an mir zieht und mich zurück halten will. Ich kann eine Postkarte mit einem simplen, kleinen Magnet an meinem Kühlschrank befestigen und sie wird nicht zu Boden fallen. Die elektromagnetische Kraft des winzigen Magnet reicht aus, um der Gravitationskraft eines ganzen Planeten dauerhaft entgegen zu wirken. Von allen vier fundamentalen Kräften der Natur – Elektromagnetismus, stark und schwache Kraft im Inneren der Atomkerne und Gravitation – ist die Gravitationskraft bei weitem und mit Abstand die schwächste Kraft. Sie spielt im Universum nur deswegen eine so dominierende Rolle, weil dort eben auch sehr viele sehr massereiche Objekte wie Sterne, Galaxien, und so weiter zu finden sind. Die Schwäche der Kraft ist also das einerseits, wenn es darum geht, warum die Gravitationskonstante so schwer zu messen ist. Das „andererseits“ ist ein wenig komplexer. Aber dazu kommen wir später noch.
Schauen wir uns zuerst einmal an, wie man die Gravitationskonstante überhaupt messen kann. Man kann es natürlich indirekt anstellen: Ich kann mir anschauen, wie sich ein Himmelskörper – zum Beispiel die Erde – um einen anderen – etwa die Sonne – bewegt. Wenn ich dann noch die Masse von Erde und Sonne bestimme und ihren Abstand messe, habe ich eigentlich schon alles, was man braucht. Aus der Bewegung kann ich die Kraft ableiten, die zwischen beiden wirken muss und mit den anderen bekannten Größen kann man dann die Gravitationskonstante berechnen. Das Problem: Es ist absolut nicht einfach, die Masse von Erde und Sonne oder ihren Abstand so exakt zu messen, dass man damit auch die Gravitationskonstante in der gewünschten Exaktheit zu berechnen. Dazu braucht man kleinere Massen und kleinere Abstände, die sich besser vermessen lassen. Aber da ist dann natürlich auch die wirkende Gravitationskraft wesentlich schwächer.
Der erste, der sich an einer direkten Messung der Gravitationskonstante versucht hat, war der britische Wissenschaftler Henry Cavendisch. Er hat es 1798 mit einem selbst erfundenen Instrument probiert, einer Gravitationswaage. Die Idee dahinter ist eigentlich simpel: Man nimmt zwei schwere Kugel, bei Cavendish waren sie knapp 1,5 Kilogramm schwer. Diese Kugeln sind verbunden, ein bisschen so wie eine Hantel und an einem Draht aufgehängt, so dass sich die ganze Konstruktion am Draht hängend drehen kann. Dann nimmt man zwei andere und schwerere Kugeln, die von außen und ein bisschen seitlich an die aufgehängten Kugeln herangeschoben werden können. Zwischen den großen und den kleinen Kugeln wirkt nun – wie zwischen allen anderen Objekten in diesem Universum eine Gravitationskraft. Die großen Kugeln ziehen die kleinen Kugeln an und verdrehen die Hantel ein kleines bisschen. Diese Verdrehung kann man messen und aus der Stärke der Verdrehung folgt – sofern man die Massen der Kugeln und ihren Abstand kennt – die Gravitationskonstante.
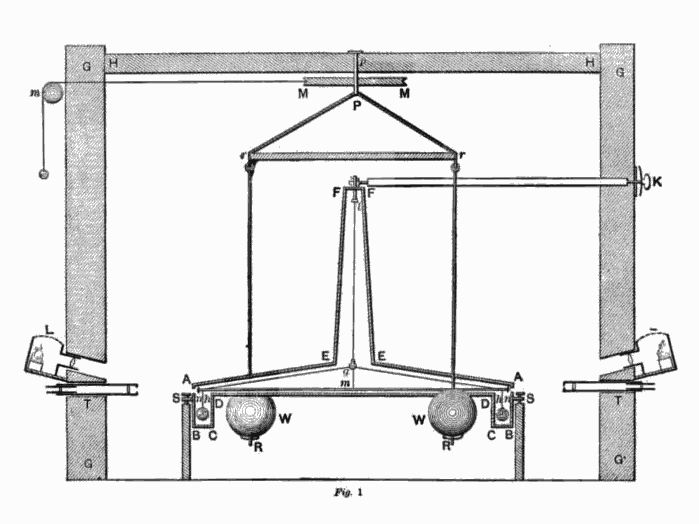
Man kann sich vorstellen, wie knifflig es ist, so ein Experiment tatsächlich auszuführen. In der Theorie mag das ja alles gut funktionieren. In der Praxis aber nicht. Den bevor man anfangen kann, muss die Kugelhantel ja VÖLLIG ruhig an ihrem Draht hängen. Ein winziger Luftzug würde schon reichen, sie in Schwingung zu versetzen. Wenn ein paar hundert Meter weit weg ein Auto vorbei fährt und den Boden minimal erschüttert, würde der Draht zu schwingen anfangen. Und so weiter. Gut, mit Autos hatte Cavendish damals kein Problem. Aber auch ein vorbeilaufender Mensch, irgendwas das zu Boden fällt oder einfach nur jemand, der neben dem Experiment steht: All das würde die Messung enorm schwierig machen bzw. unmöglich. Cavendish hat den ganzen Aufbau daher in eine Kiste gepackt. Die Kiste hat er in einen Schuppen gestellt. Alles wurde verschlossen und dann hat er erstmal gewartet, bis sich die Kugeln ausreichend still verhalten haben. Beobachtet hat er alles nur von außen und aus großer Entfernung. In der Kiste und in der Wand des Schuppens waren winzige Löcher und durch die hat Cavendish mit einem Teleskop sein Experiment kontrolliert. Der aus seiner Messung berechnete Wert der Gravitationskonstante betrug 6,74 mal 10 hoch minus 11 Kubikmeter pro Kilogramm pro Sekunde zum Quadrat. Das ist knapp ein Prozent Abweichung vom heute empfohlenen Wert. 1 Prozent Verbesserung in mehr als 200 Jahren! Wieso haben wir nicht mehr geschafft?
Das liegt nicht daran, dass wir es nicht probiert hätten. Natürlich gab es in der Zeit seit damals immer wieder neue Messungen. Am Messprinzip hat sich seit Cavendishs Zeit wenig geändert. Es geht immer noch darum, den Effekt zu messen, den zwei Massen aufeinander haben. Natürlich hat man die Methode schon ein wenig verbessert. Aber die Resultate blieben deprimierend ungenau. Verschiedene Experimente haben im Laufe der Zeit unterschiedliche Werte geliefert. Das ist eigentlich nicht ungewöhnlich in der Wissenschaft, aber man erwartet eigentlich, dass man sich immer genauer an den korrekten Wert herantastet. Bei der Gravitationskonstante kriegt man aber Werte, die nicht einmal innerhalb der Fehlergrenzen der Messung übereinstimmen. Man hat es mittlerweile dann auch mal mit komplett anderen Methoden probiert: Ohne zu sehr ins Detail zu gehen, geht es dabei darum, die Bewegung von Atomen in der Nähe einer mehr als 500 Kilogramm schweren Testmasse möglichst genau zu messen. Auch daraus kann man dann die Gravitationskonstante bestimmen und auch mit dieser komplett anderen Methode, die nichts mit den üblichen Gravitationswaagen zu tun hat, hat man Werte bekommen, die nicht mit den anderen übereinstimmen.
Womit wir jetzt beim vorhin erwähnten „andererseits“ wären. Einerseits ist es deswegen so schwer, die Gravitationskonstante zu bestimmen, weil die Gravitation so eine enorm schwache Kraft ist. Andererseits klappt es aber vielleicht auch deswegen nicht, weil wir irgendwas grundlegendes noch nicht wirklich verstanden haben! Wir wissen ja, dass die Gravitation quasi das schwarze Schaf in der Physik ist. Die anderen Kräfte lassen sich alle „quantifizieren“, also in einer quantemechanische Beschreibung formulieren und in gewissen Ausmaß auch vereinheitlichen, also zusammenführen und als unterschiedliche Aspekte einer noch fundamentaleren Kraft beschreiben. Die Gravitation aber passt überhaupt nicht mit den restlichen Kräften zusammen. Einsteins Beschreibung der Gravitation als Krümmung der Raumzeit liefert zwar extrem genaue Vorhersagen die in den letzten 100 Jahren immer und immer wieder im Experiment und in Beobachtungen bestätigt worden sind. Ebenso wie die Aussagen der Quantenmechanik. Aber eigentlich sollte es möglich sein, beide Beschreibungen der Natur irgendwie zu kombinieren. Haben wir aber nicht hingekriegt, trotzdem wir es seit Jahrzehnten intensiv versuchen. Irgendwas haben wir bei der Gravitation also nicht nicht verstanden und damit natürlich auch bei der Gravitationskonstante. Vielleicht liegt es wirklich nur daran, dass wir sehr viel genauere Messungen brauchen. Vielleicht ist es aber auch grundlegender? Vielleicht ist die Gravitationskonstante gar nicht konstant? Es gibt ja immer wieder seriöse wissenschaftliche Hypothesen, die davon ausgehen, dass sich auch Natur“konstanten“ im Laufe der Zeit ändern können. Entsprechende Beobachtungen von diversen Phänomenen im Universum wo das auffallen würde haben aber noch keine eindeutigen Hinweise geliefert. Wir können ja in der Astronomie auch in der Zeit zurück schauen; wenn wir zum Beispiel eine Supernova beobachten, deren Licht 10 Milliarden Jahre bis zu uns gebraucht hat, dann hat sie auch 10 Milliarden Jahre in der Vergangenheit stattgefunden. Wenn die Naturkonstanten damals anders waren, könnten wir das merken, wenn wir das Licht der Supernova analysieren. Haben wir bis jetzt aber nicht gemerkt… Aber vielleicht müssen wir auch hier noch genauer schauen.

Bis dahin wird uns nichts weiter übrig bleiben, als noch genauere Messungen anzustellen. 2021 hat man zum Beispiel die Gravitationskraft messen können, die zwischen zwei winzigen Kugeln wirkt, die nur wenig mehr als 90 Millimeter groß waren. Die Messung war noch viel ungenauer als die anderen; aber das war in dem Fall zu erwarten. Es ging hier vor allem darum zu zeigen, dass es überhaupt möglich ist, so eine enorm schwache Gravitationskraft _überhaupt_ messen zu können. In Zukunft geht das vielleicht genauer und wenn wir in der Lage sind, Gravitationskräfte auch auf so kleinen Skalen exakter zu messen, finden wir vielleicht auch einen Hinweis darauf, was das Problem an der Sache ist. Es ist auf jeden Fall kein akzeptabler Zustand, dass wir die Gravitationskonstante seit mehr als 200 Jahren nicht vernünftig messen können.

Vorschlag für eine Messung der Gravitationskonstante.
Man setzt zwei Eisenkugeln mit je 1kg Masse im Weltraum aus, z.B. von der ISS . Die Kugeln sind mit einem sehr dünnen Kunststsofffaden miteinander verbunden.Abstand 1m. Eine Kugel enthält einen Sender und einen Sensor, der feststellt, wenn die eine Kugel die andere berührt.
Und jetzt muss man nur noch die Zeit messen, wann das geschieht und mit der berechneten Zeit vergleichen. Die ISS kann ja das Funksignal erfassen.
Vielen Dank für den schönen Artikel.
Kleiner Fehler im Text: „…, trotzdem wir es seit Jahrzehnten intensiv versuchen.“ muss heißen „…, obwohl wir es seit Jahrzehnten intensiv versuchen“.
Viele Grüße,
Daniel.
@hwied
Und was ist, wenn die zwei Eisenkugeln, die mit einem sehr dünnen Kunststofffaden miteinander verbunden sind, eine kaum zu bemerkende Eigenrotation aufweisen? 😉
> #1 hwied, 30. April 2021
> Vorschlag für eine Messung der Gravitationskonstante.
Vom theoretischen Standpunkt aus ist die Gravitationskonstante irrelevant: G lässt sich konsistent = 1 setzen.
https://onlinelibrary.wiley.com/doi/pdf/10.1002/phbl.19990551109
Ich meine ja immer noch, dass wir die Gravitation wesentlich besser verstehen könnten, wüssten wir nur endlich einmal, was dieser vermaledeite „Raum“ eigentlich sein soll. Erst dann kann man schließlich wissen, warum er eigentlich von Massen gekrümmt wird.
Karl-Heinz
ok. Wir verzichten auf den Faden und nehmen nur eine Kugel, die im Abstand von 100 m in der Umlaufbahn der ISS ausgesetzt wird. Dann messen wir kontinuirlich mit dem Laser den Abstand zur ISS.
Karl Mistelberger,
Der praktische Nutzen mag gering sein, aber denken wir an den Mond. Wir stationieren eine besetzte Station auf einer geostationären Bahn. Dann lassen wir eine Eisenkugel auf die Mondoberfläche fallen. Die Kugel fällt dann nicht in einer Spirale auf den Mond, sondern senkrecht . Dann brauchen wir nur noch zu rechnen. Nachtrag, es wird alle allerdings sehr schwierig die passende Landestelle zu finden, weil die Oberfläche des Mondes nicht eben ist und wir auch noch den Abstand zum Mondmittelpunkt errechnen müssen. Aber als Anregung für angehende Hobbyastronomen doch brauchbar.
@hwied
Die ISS muss mitunter regelmäßig angehoben werden, da in 400 km Höhe noch kein reines Vakuum herrscht. Ich befürchte, dass dies große Auswirkung auf die Messgenauigkeit hat. 😉
„“2021 hat man zum Beispiel die Gravitationskraft messen können, die zwischen zwei winzigen Kugeln wirkt, die nur wenig mehr als 90 Millimeter groß waren.““
Ach was!
Die Kugeln,
die an dem Eötvös -Apparat 1965 an der Wand unseres Physiksaales hingen, waren schon etwas kleiner!
@hwied
Du meinst also eine geostationäre Raumstation um den Mond, oder? Und von dort willst du eine Kugel auf den Mond fallen lassen. Ich finde es lustig, dass die Kugel senkrecht nach unten fallen soll, aber die Raumstation an ihrem Ort bleibt. 😉
Karl-Heinz,
schon klar, es geht um das Messprinzip.
Wir können auch einen Satelliten in eine Erdumlaufbahn bringen, der der Erde um die Sonne vorauseilt oder hinterherlläuft. Abstand 1 Million km.
Und wenn er sich bis auf 500 000 km der Erde genähert hat, messen wir die Zeit.
Das Problem ist der Mond, was machen wir mit dem ?
Korrektur
Erdumlaufbahn ist falsch , es muss Sonnenumlaufbahn heißen.
Karl-Heinz,
du bist schon ein harter Brocken.
Also gut. Die neue Lösung ist noch billiger.
Wir verzichten auf die Station in der Mondumlaufbahn und geben dem nächsten Mondastronauten ein Spezialgewehr mit.
Der schießt senkrecht nach oben , mit dem Laser wird festgestellt wie groß die Steighöhe ist und dann wird die Fallzeit der Spezialkugel gemessen. Bingo!
„“Der praktische Nutzen mag gering sein, aber denken wir an den Mond. Wir stationieren eine besetzte Station auf einer geostationären Bahn. Dann lassen wir eine Eisenkugel auf die Mondoberfläche fallen. Die Kugel fällt dann nicht in einer Spirale auf den Mond, sondern senkrecht .““
Geostationär statt selenostationär
kann man noch verzeihen, Das ist nur „klassische Bildung“
Aber „fallen lassen“, und das senkrecht auf den Mond,
ist ein starker Tobak.
@Kerberos
Ja genau!!! 😉
Jetzt ist es Forschern erstmals gelungen, die winzige Gravitationskraft zwischen nur zwei Millimeter großen und gut 90 Milligramm schweren Goldkugeln zu messen. Es ist die kleinste jemals gemessene Gravitationskraft.
In der Bahnhöhe der ISS gibt es einen wenn auch geringen Luftwiderstand, weshalb deren Orbit immer mal wieder angehoben werden muss. Mit einer G-Messung im All müsste man also sehr viel weiter weg von der Erde. Vielleicht in die Gegend, die für das Gravitationswellenexperiment (hieß das LISA?) vorgesehen ist, das hat ja dasselbe Problem.
Das Wort „trotzdem“ hat man früher mal wie „obwohl“ benutzt. Alt, aber nicht falsch.
Andere Frage: „Winzige“ Kugeln mit 90 Millimetern Durchmesser?
Hallo, hast du noch nichts von Anfangsschwierigkeiten gehört. Wir sind beim Brainstorming und was machst du, du zerstörst meine schönsten Träume.
Es bleibt dabei, wir schießen von der Mondoberfläche nach oben.
Wenn man bedenkt, dass jedes Atom im Universum über die Gravitation mit jedem anderen Atom verbunden ist, könnte es Titanen schwindlig werden. Mir gefällt irgendwie die Vorstellung, hier die Wirkung Mephistos zu spüren der alles was entstand wieder rückgängig machen und an einen Punkt zusammenziehen will ; )
@ an alle, die es so nicht mit der klassische Bildung haben, einschließlich mir.
Selene
eine Mondgöttin der griechischen Mythologie
Es ist doch ganz einfach:
Wir werfen eben mal alle ungeeigneten Vorschläg zur Messung der Gravitationskonstante auf einen Haufen.
M. E. n. dürfte es nicht lange dauern, bis dadurch ein Schwarzes Loch entsteht, mit dem man dann wunderbare Experimente zur Messung der Gravitationskonstante anstellen könnte.
Kyllyeti,
du sprichst mir aus der Seele. Mir ist gerade bewusst geworden, dass es kein Fleckchen gibt, wo es keine Gravitation gibt.
Rob,
wir vergessen auch , dass Atome gar nicht alle gleich sein müssen. Das ist einfach nur eine Annahme. die können auch Beziehungen untereinander eingehen, wie bei uns Menschen. Und deren Bindungen sind stärker als bei Menschen.
@hwied
Mit der Idee, auf dem Mond mit dem Gewehr senkrecht nach oben zu schießen und anschließend die Fallzeit zu messen, kannst du höchstens die Mondbeschleunig bestimmen.
An die Gravitationskonstante kommst du nicht ran, den dazu müsstest du den inneren Aufbau des Mondes wirklich sehr genau kennen.
Liegt das nicht daran, dass Cavendish (für die damalige Zeit) so unglaublich genau gearbeitet hat? Da können wir uns anstrengen wie wir wollen, „viel“ können wir dann nicht mehr daran ändern.
Wobei, und das klingt schon etwas paradox, wenig hier schon viel bedeuten würde. Ändert sich erst in der 4ten, 5ten, 6ten,… Stelle hinter dem Komma etwas, was ja nur ganz wenig wäre, dann hätte man die Genauigkeit doch schon um etliche Zehnerpotenzen verbessert, allerdings mit negativen Exponenten, was dann doch wieder nur wenig wäre.
Wie sagt man, in so einem Zusammenhang eigentlich, was man wirklich sagen will?
Karl-Heinz,
dein Argument ist logisch. Auch der senkrechte Schuss nach oben bleibt nicht senkrecht, es gibt eine Parabel.
Das ist wie verhext, nichts im Weltraum ist gerade.
Die ganzen Ideen mit dem Mond kranken auch noch an einem anderen Problem: Wir müssten die Mondmasse mindestens so genau kennen wie wir G messen wollen. Ich kann in meinem Labor zwar problemlos auf sechs Stellen wiegen, mit Mühe und Umsicht auch noch genauer – aber der dumme Mond passt einfach nicht durch die Tür. Und, man müsste voraussetzen, dass die Massenverteilung ausreichend genau radialsymmetrisch ist – dummerweise ist das ausgerechnet bei den beiden erreichbaren Körpern nicht sicher, bei der Erde mit den Kontinentalplatten, beim Mond mit den Maaren.
„“Auch der senkrechte Schuss nach oben bleibt nicht senkrecht, es gibt eine Parabel.““
Auch das ist falsch, wie schon Kepler wußte.
Hallo Chemiker,
aus der Libration des Mondes müsste man eigentlich
die Massenverteilung ermitteln können.
Gelesen hab ich dazu noch nichts.
*ächz*
@Chemiker:
Wenn ich mich recht erinnere, wird der Plural „Maria“ verwendet. Mit wichtiger Ansage: Betonung auf der ersten Silbe. Also nicht wie der weibliche Name.
(Aber wann braucht man das auch mal … wenn man nicht gerade Geo-, äh, Selenologie aufm Zertifikat hat.)
Bullet
nach Maaren bist du auch aufnahmefähig für die Beziehungen zwischen Atomen. Fast alle sind eine Mischung aus Nukliden, also, dem unterschiedlichen Anteil an Neutronen. So gibt es C 12 mit 6 Protonen und 6 Neutronen. Es gibt auch C 14 , das 6 Protonen und 8 Neutronen hat. Dieses Kohlenstoffatom ist schwerer als C 12 und es entsteht aus N 14. Das ist Stickstoffgas. Das verwandelt sich durch Sonneneinstrahlung in C 14. Und da Stickstoff als N² vorkommt kann man von einer Bindung sprechen. Und jetzt kommt ein Sonnenstrahl und bricht diese Bindung auf. Wir haben ein Kohlenstoffsingle C 14 und ein Stickstoffsingle N 14. Und wenn jetzt ein Wasserstoffsingle dazukommt, H dann bekommen wir einen Dreier C-N-H Cyanwasserstoff und der ist giftig.
Das toppt sogar die menschlichen Beziehungen.
selenophile …
Sind das also jene, die Selen lieben oder doch den Mond? 🙂
Selen ist erst seit 1957 als essentielles, also lebenswichtiges Spurenelement bekannt. Im Körper spielt es eine wichtige Rolle für die Entgiftung, ist Bestandteil einer Reihe von Enzymen und beeinflusst den Stoffwechsel der Schilddrüse. Seinen Namen verdankt das Metall dem lateinischen Wort „selene“ für Mond. Sicher gibt es auch Selen auf selene.
In Halbleiter braucht man auch Selen, die Freunde der Elektronik können wir auch Halbsenologen nennen.
Seit längerem sind die Seleniten bekannt. Das weiß auch die Wiki, ist also Allgemeinwissen. 😉
https://de.wikipedia.org/wiki/Die_ersten_Menschen_auf_dem_Mond
Seltsam, dass mir das erst jetzt auffällt:
Genau wie bei den Homöopathen *schenkelklopf* Das macht es doppelt doof 🙂
> #3 Karl-Heinz, Graz, 30. April 2021
> Und was ist, wenn die zwei Eisenkugeln, die mit einem sehr dünnen Kunststofffaden miteinander verbunden sind, eine kaum zu bemerkende Eigenrotation aufweisen?
Freier Fall ist selbst im Weltraum problematisch. Den Dilettanten kümmert es nicht. Der Experte treibt beachtenswerten Aufwand, um ihn zu verwirklichen:
http://einstein.stanford.edu/STEP/information/data/testq2.html
Kurze Frage: Es gibt ja diese elektrische Universum Typen die immer behaupten die elektromagnetische Kraft sei das alles Bestimmende. Das ist natürlich Quatsch aber die Frage warum das Quatsch ist, kann man glaub ich nicht damit beantworten, das es im Universum dicke Brummer gibt. So ein Magnetar hat ein enorm starkes Magnetfeld, was geladene Teilchen sicher mehr beeinflusst als die dennoch enorme Anziehungskraft des Neutronensterns.
Ist die Begründung für die Gravitation als bestimmende Kraft nicht eher, dass Gravitation nicht abschirmbar ist aber die elektromagnetische Kraft durch Quantefluktuationen in größeren Skalen komplett abschirmt wird?
Könnte es sein, dass Dunkle Materie (oder Dunkle Energie) die Gravitationskonstante beeinflussen?
Da unser Sonnensystem innerhalb der Rotationsscheibe der Milchstraße pendelt, könnte sich der Einfluss der Dunklen Materie sich im laufe der Zeit auch ändern.
Gibt es eine Timeline all der Messungen? Und was kann man da herauslesen?
@René Kern:
Ja, aber Quantenfluktuationen sind nicht die Ursache. Es liegt daran, dass es beim Elektromagnetismus zwei Vorzeichen der Ladung gibt, wobei sich Ladungen mit dem gleichen Vorzeichen abstoßen und Ladungen mit unterschiedlichem Vorzeichen anziehen. Bei der Gravitation gibt es nur ein Vorzeichen und alles zieht sich an.
Gravitativ gesehen ist ein Stern eine große Ansammlung von Teilchen deren „gravitative Ladung“ (d.h. Masse) das selbe Vorzeichen hat (weil es nur ein Vorzeichen gibt). Weil die sich alle gegenseitig anziehen, ist eine solche Konfiguration stabil (vorausgesetzt es gibt auch noch eine Kraft nach außen). Das elektromagnetische Äquivalent davon, also z.B. eine große Ansammlung von Protonen ohne Elektronen oder andere negativ geladene Teilchen, ist hingegen nicht stabil. Und wenn man Elektronen dazugibt um das Objekt zu stabilisieren, reduziert das die effektive Ladung.
Warum sollten große Ansammlungen gleicher Ladungen nicht stabil sein? Brauche ja nur ein elektromagnetisches Feld anlegen und schon trennen sich die Ladungen. Gedankenexperiment: Die könnte ich dann im Vakuum separieren und jeweils in einen Kasten stecken. Schon hätte ich viele Ladungen mit gleichen Vorzeichen an „einem“ Ort. Diese würden dann ja eine Anziehung auf die Ladungen mit entgegengesetzten Vorzeichen wirken wenn ich die Kästen öffne. Entferne ich aber die Ladungen sehr weit voneinander im Vakuum wird sich aber auf großen Skalen die Anziehungskraft der elektromagnetischen Kraft nicht mehr mit dem Quadrat des Abstandes abnehmen sondern mehr, da Quantefluktuationen zwischen den Ladungen ausrichten werden und so die Kraft abschirmen.
@René:
Weil sie sich gegenseitig abstoßen.
Quantenfluktuationen spielen hier überhaupt keine Rolle. Als Faustregel: Quanteneffekte sind auf kleinen Skalen relevant (speziell: wenn Wirkungsdifferenzen im Bereich des Wirkungsquantums sind), nicht auf großen Skalen.
@René
Dann versuch mal 1 kg pure Elektronen in einen kugelförmig Kasten von einem Liter zu stecken. Welche Energie ist dafür nötig, die einem jederzeit um die Ohren fliegen kann. 😉
@Rene:
Soetwas gibt es nicht.
Das ist Unsinn.
*seufz*
Lies ein Physikbuch.
Bitte.
„“Lies ein Physikbuch. „“
Das nützt nix bei Fluktuationen im Hirn.
@René
Für große Abstände kannst du die Auswirkung der Vakuumpolarisation vernachlässigen, denn sie nimmt mit der Entfernung rapide ab!
Ein Elektron, dass ein Wasserstoffatom umkreist, hat durch die Vakuumpolarisation nur mehr eine Potentialabweichung in der Größenordnung von 10^(-125).
Für größere Abstände als, ich sag mal Atomdurchmesser um eine Größe zu nennen, kannst die Vakuumpolarisation vergessen.
Stammt die Idee der Vakuumpolarisation auf größeren Skalen von dir, oder hast du sie von jene, die ein elektrische Universum propagieren. 😉
https://de.m.wikipedia.org/wiki/Uehling-Potential
Das ganze Theater mit Gravitation ist ja auch ein Theaterproblem:
Wir haben da vier Schauspieler. Einer stellt eine hoch konzentrierte Figur dar, die mit sich selbst beschäftigt ist (starke Kernkraft). Der zweite ist zerstreut und vergesslich (schwache Kernkraft). Der dritte ein Charismatiker (Elektromagnetismus). Und der vierte übergewichtig (Gravitation).
Die ersten drei sind charakterlich definiert, der vierte nicht, bei ihm ist es eine körperliche Eigenschaft. Und dann wirkt sie auch nicht nur auf die Zuschauer sondern unmittelbar auf die Bühne.
Also stellt sich der Zuschauer die Frage, was das mit dem vierten soll. Wie passt er zum Rest? Und er fragt sich, welche Rolle die Bühne hierbei spielt, was sie eigentlich ist. Tja, was ist Raum und Zeit?
Adam,
es muss heißen, der vierte ist übergewichtig und gleichzeitig der Regisseur.
@Karl Heinz
Woher ich das habe? Von hier https://youtu.be/brcb32kkusE
So ab 2 Minuten.
Der gute ist jedenfalls kein Hobbyphysiker. Mag ja sein, dass ich hier ein wenig was durcheinander gewürfelt habe aber im Video wird gesagt, dass je weiter ich von der Ladung weg bin, desto größer ist die Abschirmung.
Ich muss schon sagen hier herscht ja ein ziemlich rauer Wind. Mag sein dass ich mir hier ein wenig Unsinn zusammengereimt habe aber muss man da gleich so aggressiv antworten und mich zu den VTlern stecken? Bin ich nämlich nicht.
@René
Danke für die Info. Ich schaue mir das genauer an. 🙂
@René:
Was in dem Video besprochen wird spielt sich alles auf mikroskopisch kleinen Längenskalen ab. Wenn von „größeren Entfernungen“ die Rede ist, sind damit immer noch Abstände gemeint, die kleiner sind als der Durchmesser eines Atoms. Die relevante Längenskala für diese Effekte ist die Compton-Wellenlänge des leichtesten geladenen Teilchens, also des Elektrons.
Oder anders ausgedrückt: Wenn man die wirklich im Experiment gemessene elektrostatische Kraft mit der aus dem Coulomb-Gesetz vergleicht, bekommt man nur dann eine Abweichung, wenn der Abstand wirklich extrem klein ist. Im gesamten makroskopischen Bereich (und den kann man hier wirklich schon bei der Größe von Molekülen anfangen lassen) gibt es keinerlei Abweichungen durch „Quantenfluktuationen“. (Ich finde diesen Begriff etwas unglücklich, weil er eine Dynamik suggeriert, die in der Realität nicht existiert. Der Vakuumzustand ist auch in der QFT statisch.)
Ahh das ist doch eine vernünftig nachvollziehbare und freundliche Art meine Verwirrung aufzulösen. Viele Dank Jan und Karl Heinz.
Nach meiner Meinung kommt es unterhalb der Compton-Wellenlänge beim Atom im Kern, genau wie in der Sonne, zu Herzkurven mit resonantem atmen des Torus im Kern-/Sonnendurchmesser über Einflüsse der Änderung der Position des Mittelpunktes des Kerns bzw. der Sonne sowie durch den Einfluss der Position des Elektrons bzw. der Erde und aller anderen Satelliten. Eine annähernde Selbstähnlichkeit der Raumzeit zeigt sich beim Messen in den Wiederholungen des sogenannten Rauschens bei den Signalen aus allen Richtungen als wiederholende Apfelmännchen in allen Frequenzbereichen. In den fraktalen Strukturen dieser Frequenzen der Wiederholungen, sowie am Rand der gemessenen Knospen bzw. Herzkurven finden sich verkleinerte ungefähre, also nicht ganz exakte, Kopien der gesamten Mengen als Satelliten, wobei jeder Ausschnitt unendlich viele dieser Satelliten enthält. Unmittelbar am Rand eines Satelliten treten fast die gleichen Strukturen auf wie an den entsprechenden Stellen des Originals. Diese Strukturen sind nur bei extremer Vergrößerung erkennbar.
@Bernd Nowotnick
Nix bla bla
Bitte Rechnen und Lösen her Ingenieur 🙂
Welche Energie muss man aufwenden, wenn man versucht 1 kg pure Elektronen in ein kugelförmiges Behältnis von einem Liter zu stecken.
# 52
Die (Wert-) Felder, z.B. ein Elektron (- Schulden) oder ein Positron (+ Guthaben), haben mit der Dynamik von einzelnen Vektoren, bspw. den jeweiligen Abstand der Position des Mittelpunktes des Feldes mit der zugehörigen Richtung in der Zeitentwicklung im Verhältnis der zugehörigen Dimensionen zum Umfeld – eventuell einer Abschirmung oder Ablenkung – wie dem Mittelpunkt des Kerns, und nicht absolut mit den statischen Definitionen der Eigenschaften einer (dreier) Dimension zur Orientierung des Ausgangs- bzw. Augenblickbezuges zur Reihenentwicklung in den zugehörigen Dimensionen des gerade aktuellen Problems des Feldes zu tun.
BN
bevor du rechnest, überlege, wieviel 1 kg Elektronen kosten, ob du dir das leisten kannst.
K-H
Baust du wieder eine Elektronenbombe ?
Elektronenbombe ist gut.
Falls ich mich nicht verrechnet habe.
Wenn ich 1 kg Elektronen in ein Volumen von 1 m^3 stecke, muss ich dafür eine Energie von 2,7 * 10^32 J aufwenden. Das ist eine gigantische Energiemenge.
Ich habe es nach der Formel berechnet. Der Fachbegriff dafür ist Bindungsenergie.
E = 3 / (20 π ε_0 ) * Q^2 / R
@Bernd Nowotnick
Mein Eindruck von dir. Du hast schon lange nichts mehr auf diesem Gebiet gemacht. Was bleibt und noch immer funktioniert ist dein Schwurbeln. 😉
Karl-Heinz
Dein Vorschlag 1 kg Elektronen einzusperren war ein sehr kluger Gedanke. Zwingt er doch, über das Wesen der Elektronen nachzudenken.
Also, 1kg Elektronen entsprechen etwa 10 hoch 30 Elektronen.
1 mol Elektronen = 6,02 mal 10 hoch 23 Elektronen.
1 mol Elektronen = 96 486 As
Umgerechnet auf 10 hoch 30 Elektronen sind das 1,64 mal 10 hoch 11 As
Wenn jede Sekunde 1 A fließt dann braucht man 500 Jahre um diese 1,64 mal 10 hoch 11 As in einen Behälter zu sperren.
Was du da verlangst, das ist ein Langzeitprojekt.
Wie groß der Behälter sein muss, bei einer bestimmten Flächenladungsdichte/Raumladungsdichte , das kommt als nächstes dran. Ob man 1 kg Elektronen kaufen kann, klar, das geht, ist gar nicht so teuer.
1 m³ Raum reicht wahrscheinlich nicht . Muss ich noch überdenken !
Karl-Heinz
Kannst du mal die Formel mit E erklären !
Auf jeden Fall muss die Spannung bei der Ladungsdichte sehr hoch sein. viel zu hoch, um sie isolieren zu können.
Nachtrag Karl-Heinz
Deine Berechnung ist richtig. Man braucht etwa 10hoch 32 Joule.
Meine Formel : U = k null mal Q ² / 2 R
Oder etwas anschaulicher, man braucht etwa 3 Erdoberflächen um 1 Kg Elektronen zu verteilen, ohne dass eine Entladung stattfindet.
@hwied #57
Also E ist die Energie bzw. die Arbeit die man rein stecken muss. Man bringt zwei Elektronen aus dem Unendlichen auf einen Abstand D. Da sich die Ladungen abstoßen, muss man dafür Energie aufwenden. Nun holt man ein drittes Elektron aus dem Unendlichen dazu. Man beachte, dass das dritte Elektron jetzt gegen das Kraftfeld der beiden anderen anlaufen muss. Und weiter geht es mit dem vierten Elektron und dann mit dem fünften Elektron usw.
Der mathematischer Ansatz um die Formel E = 3 / (20 π ε_0 ) * Q^2 / R herzuleiten ist dann aber doch ein bisschen anders. Ich habe den eleganten Ansatz aus dem Gebiet der Astronomie. Das elektrostatische Feld und das Gravitationsfeld sind sich ja sehr ähnlich.
Natürlich kann man das Gedankenexperiment in Wirklichkeit nie und nimmer realisieren.
Du weißt ja, dass unsere Erde zu Beginn rot glühend war, als gravitative Energie aus der Akkretion der ursprünglichen Materials frei wurde. Wir liegen bei unserem Beispiel mit 1kg Elektronen in einem Kubikmeter bezüglich Energie in der selben Größenordnung!
K-H
nie und nimmer,
also, ich habe mal gegoogelt und diesen Artikel gefunden.
100 kg Wasserstoffgas kosten an einer Wasserstoffttankstelle nur 9,50 €.
Wenn man weiß, dass ein Proton 1830 mal schwerer ist als ein Elektron, dann braucht man nur 1830 Kg Wasserstoff zu kaufen und schon hat man 1 kg Elektronen mit gekauft. Und….darauf kommt es an, man kann die Elektronen gewinnen, indem man den Wasserstoff ionisiert. Man braucht 13,2 eV pro Elektron bzw. Atom.
@hwied
Na ja, das ist die Ablösearbeit des Elektrons vom Atom. Jetzt bitte das ionisierte Gas ins Unentgeltliche verfrachten. Das abgelöst Elektron behalten wir. Viel Spaß bei diesem Versuch.
K-H
Du hast erkannt, wo die Schwachstelle ist. Vorschlag auf die Schnelle. Wir erhitzen einen Druckbehälter mit Wasserstoffgas. Der Behälter bleibt geschlossen.
Die Wand des Behälters ist von derart, dass die Poren kein H Ion durchlassen, aber die Elektronen doch. Wir brauchen nur noch eine schnelle Drehung und durch die Zentrifugalkraft driften die Elektronen nach außen und brauchen nur noch abgegriffen zu werden.
Schöner Sonntag!
@hwied
Verstehe.
Du sammelst die Elektronen ein und fährst mit den Elektronen von dannen.
Bist noch nie auf den Gedanken gekommen, dass du durch das Wegfahren eine Ladungstrennung vornimmst?
Nicht vergessen auf Muttertag 😉
@hwied
Neben der Ladungstrennung gibt es auch die Massentrennung. Wenn du dich vom Wirtshaus entfernst, so ist die Kraft ausgehend vom Wirtshausgebäute kaum merkbar. Wenn du aber auf den Berg begibst und damit dich von der Erde entfernst, das merkst schon. Das darfst mir glauben, du Flacherdler. 😉
@Karl-Heinz:
Ich nehme mal an, dass das ein Vertipper war.
Wenn, dann wars ein schöner 🙂
@Robert:
Deren Ladung sich mit der der Protonen aufhebt. So dass man ein Kilo neutral geladenes sonstwas hat.
Aber den Denkfehler hast du wohl schon selbst erkannt. Jedenfalls so halbwegs. (Was ganz erstaunlich ist.)
PDP 10,
1 kg Elektronen aus der Steckdose zu holen, das kann jeder. Sie aber an der Tankstelle zu kaufen, das macht nicht jeder. Und das ergibt auch erst dann einen Sinn, wenn man die Elektronen dann durch die Ionisation von H2 gewinnt.
Wenn du dich schon als „Wissender“ outest, wie würdest du größere Mengen von Elektronen speichern, ich meine jetzt nicht als Flächenladung in Kondensatoren oder eingesperrt als Elektronengas in Kupferleitungen ?
Karl-Heinz,
Über die Ladungstrennung sind wir hinaus, besser gesagt, wir sind mittendrin, denn es geht mir um das Plasma.
Die Plasmaforschung wird darüber entscheiden, ob wir mit der Kernfusion weiterkommen.
Ionisation durch thermische Anregung oder mit Laser sind bekannt.
Eine andere Möglichkeit ist die Herstellung eines Tieftemperaturplasmas. Gerade habe ich gelesen, dass die Entstehung von Cooper-Paaren bis zu einem Anteil von 50% bei freien Elektronen möglich ist. Und da Cooper Paare wie Bosonen wirken, stoßen sie sich nicht gegenseitig ab. Und genau das wollen wir bei der Speicherung von freien Elektronen.