Kryptologie jenseits der Verschlüsselung

Dieser Artikel ist Teil des ScienceBlogs Blog-Schreibwettbewerb 2017. Informationen zum Ablauf gibt es hier. Leserinnen und Leser können die Artikel bewerten und bei der Abstimmung einen Preis gewinnen – Details dazu gibt es hier. Eine Übersicht über alle am Bewerb teilnehmenden Artikel gibt es hier. Informationen zu den Autoren der Wettbewerbsartikel finden sich in den jeweiligen Texten.
——————————————————————————————————————
Kryptologie jenseits der Verschlüsselung

von Christian Henrich

Seitdem ich das Buch Geheime Botschaften von Simon Singh gelesen habe, bin ich von der Kryptologie fasziniert. Ich habe am Karlsruher Institut für Technologie (KIT) als Doktorand im Bereich kryptographische Wahlverfahren promoviert und gehöre zu der Arbeitsgruppe, die 2008 mit dem Deutschen IT-Sicherheitspreis für das kryptographische Wahlverfahren Bingo Voting ausgezeichnet wurden.

Die moderne Kryptologie hat viel mehr zu bieten als nur Geheimschriften. Zwei wichtige Werkzeuge der modernen Kryptologie möchte ich hier präsentieren. Commitments legen eine Zahl fest, ohne sie zu verraten. Zero-Knowledge-Beweise überzeugen jemanden von der Korrektheit einer Aussage, ohne irgendetwas anderes zu enthüllen.

Kryptologie lässt die meisten an Geheimschriften und Verschlüsselungsverfahren denken. Und bis weit in das letzte Jahrhundert hinein war das Bild damit auch (fast) vollständig. Inzwischen hat sich die Kryptologie weiterentwickelt und bietet mehr als Verschlüsselungsverfahren, die nur ein Teilgebiet der Kryptologie darstellen. Alle Gebiete nutzen Mathematik, was den interessierten Laien leider oft abschreckt, so dass die moderne Kryptologie nicht die Aufmerksamkeit erhält, die sie meiner Meinung nach verdient. Viele kennen bestimmt digitale Signaturen, die Dokumente gegen unbemerkte Veränderung schützen. Recht bekannt sind noch Kryptowährungen wie Bitcoin.
Wenige kennen jedoch sichere Mehrparteienberechnungen, die in diesem YouTube-Video an einem einfachen Beispiel erklärt werden.
Aber selbst das ist noch nicht alles, was die moderne Kryptologie vermag. Mit diesem Text möchte ich zwei erstaunliche Werkzeuge vorstellen und daran aufzeigen, was die Kryptologie noch zu bieten hat.

Commitments
Als Motivation für die beiden Werkzeuge der modernen Kryptologie schauen wir uns folgendes Problem an: Alice ist Bürgermeisterin einer mittelgroßen Stadt und möchte den Auftrag für den Bau des neuen Rathauses vergeben. Dazu führt sie ein Bieterverfahren durch, bei dem ein Gebot aus einer einzigen Zahl, den Kosten für den Bau, besteht. Für Alice ist natürlich das günstigste das beste Angebot. Die Firmen von Bob, Carol und Dave sind an dem Auftrag interessiert und möchten ein Gebot abgeben. Damit die anderen Interessenten das Gebot nicht erfahren, will jeder sein Gebot verschlüsselt abgeben, so dass nur Alice und ihre Mitarbeiter die Gebote erfahren.

Es gibt jedoch eine Komplikation. Eve ist die Nichte von Dave und arbeitet für Alice in der Abteilung, die den Bauauftrag vergibt. Um einen möglichen Einfluss auf das Bieterverfahren zu verhindern (indem Eve die Gebote der Mitbewerber an Dave verrät) verwendet Alice statt Verschlüsselung ein anderes Werkzeug der Kryptologie, nämlich Commitments.

Ein Commitment, zu deutsch etwa Festlegung, erlaubt es einem Sender, sich bei einem Empfänger auf einen Wert festzulegen, ohne dem Empfänger den Wert mitzuteilen. Ein solches Commitment-Verfahren besitzt zwei Eigenschaften: Es ist verbergend, der Empfänger sieht dem Commitment also nicht an, welcher Wert darin steckt, und es ist verbindlich, der Sender hat sich mit Abgabe des Commitments festgelegt und kann sich nicht nachträglich umentscheiden. Wir schauen uns hier ein konkretes Verfahren an, das zusätzliche Eigenschaften besitzt, die wir später noch brauchen. Das Verfahren trägt den etwas unhandlichen Namen unconditionally hiding discrete logarithm commitment, kurz UHDLC, und wird auch als Pedersen-Commitment bezeichnet.

Da wir die Funktionsweise im Detail verstehen wollen, schauen wir uns das Verfahren an, wie es mit Farben funktionieren würde. Stellen wir uns vor, Alice besitzt einen Farbkasten mit vielen Farben. Von diesen Farben ist ein Teil jedem möglichen Wert eines Gebots zugeordnet. Die übrigen Farben sind nicht zugeordnet. Aus diesen Farben mischt jeder Bieter einen Farbton und gibt diesen als Commitment ab.

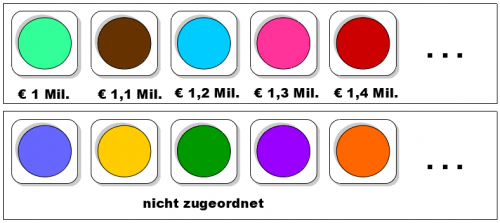
Für die Abgabe seines Gebots erzeugt Bob ein Commitment mit seinem Gebot als Inhalt. Dazu mischt er die Farbe, die seinem Gebot zugeordnet ist, mit ein paar von den nicht zugeordneten Farben. Der Farbe, die Bob dann erhält, sieht man nicht mehr an, welche der zugeordneten Farben er verwendet hat. Wer schon einmal einen Farbton nachmischen wollte, um die fehlende Wand in einem in Pastellgrün gestrichenes Zimmer zu streichen, kann bestätigen, wie schwierig es ist, aus einer Farbe das exakte Mischungsverhältnis der Grundfarben zu bestimmen. Damit ist das Commitment, also die von Bob gemischte Farbe, schon einmal verbergend.

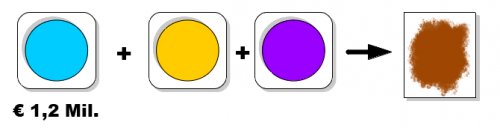
Mit der Abgabe des Commitments liegt das Gebot fest. Nachdem alle Bieter ihre Commitments abgegeben haben und damit alle Gebote festliegen, sendet jeder Bieter sein Gebot direkt an Alice, damit diese das beste Gebot auswählen kann. Um zu verhindern, dass die Gebote bekannt werden, nutzen sie dazu Verschlüsselungsverfahren. Da die Gebote jetzt festliegen, kann Eve keinen Einfluss auf das Verfahren mehr nehmen.

In unserem Beispiel hat Bob das beste Angebot abgegeben und das Bieterverfahren gewonnen. Alice gibt diese Entscheidung bekannt und Bob öffnet sein Commitment. Dazu nennt Bob sein Gebot und damit auch die zugeordnete Farbe, sowie die hinzugemischten nicht zugeordneten Farben. Nun prüft jeder der anderen Bieter zwei Dinge: Erstens mischt jeder die Farben von Bob zusammen und prüft, ob die resultierende Farbe das Commitment von Bob ergibt. Und zweitens sieht jeder Bieter sofort, ob das Gebot von Bob wirklich besser als das eigene war. Schauen wir uns beides im Detail an.

Bob hat sein Commitment geöffnet und die Farben genannt, aus denen er sein Commitment gemischt hat. Alice als Auftraggeberin sowie die Mitbewerber Carol und Dave prüfen, ob die von Bob angegeben Farben gemischt den gleichen Farbton ergeben, wie ihn sein Commitment hatte. Das menschliche Auge ist sehr gut darin festzustellen, ob zwei Farben gleich oder auch nur leicht unterschiedlich sind. Außerdem prüfen sie, ob Bob korrekt die zu seinem Gebot zugeordnete Farbe verwendet und keine andere einer anderen Zahl zugeordnete Farbe verwendet hat. Dies ist wichtig damit das Commitment-Verfahren verbindlich ist. Für Bob ist es praktisch unmöglich, zwei Farbkombinationen zu finden, die unterschiedliche (und jeweils eine) zugeordnete Farben beinhalten, aber trotzdem am Ende den gleichen Farbton als Commitment ergeben. Das aber bräuchte Bob, um ein Commitment auf zwei verschiedene Weisen öffnen zu können. Damit ist das Commitment für Bob, und analog für jeden anderen, verbindlich. Oben haben wir bereits gesagt, dass das Commitment-Verfahren verbergend ist, also besitzt das Commitment-Verfahren beide geforderten Eigenschaften.

Die Tatsache, dass das Commitment-Verfahren verbindlich, hilft uns auch beim nächsten Aspekt. Nachdem Bob sein Commitment geöffnet und damit sein Gebot bekannt gegeben hat, sehen Carol und Dave als Mitbewerber sofort, ob ihr eigenes Gebot besser war oder nicht. Im Streitfall helfen ihnen die Commitments, die Vergabe anzufechten. Falls Carol beispielsweise ein besseres Gebot abgegeben hätte, kann sie ihrerseits ihr Commitment öffnen und damit beweise, dass ihr Gebot besser war als das von Bob, und zwar bevor sie das Gebot von Bob erfahren hat. Da sie ihr Commitment abgegeben hatte, bevor Bob sein Gebot genannt hat, kann sie ihr Gebot nicht nachträglich verändert haben.

Die Eigenschaften der Farben in unserem Beispiel klingen vielleicht etwas weit hergeholt.
In der Welt der Mathematik müssen wir nicht auf Farben zurückgreifen, sondern benutzen spezielle mathematische Strukturen, nämlich zyklische Gruppen, in denen das Problem des diskreten Logarithmus schwer zu lösen ist. Die gleichen Strukturen werden von einigen Verschlüsselungs- und Signaturverfahren benutzt, bieten genau die Eigenschaften, die wir hier für das Commitment-Verfahren benötigen, und sind gut untersucht. Ein anderes berühmtes Verfahren, das diese Strukturen nutzt, ist der Diffie-Hellman-Schlüsselaustausch. Es gibt ein YouTube-Video und einen Artikel dazu (beides auf Englisch), bei denen ebenfalls das Verfahren mit Farben erklärt wird.
Aber zurück zu unseren Farben.

Das Beimischen der nicht zugeordneten Farben dient nicht nur dazu, den Inhalt des Commitments zu verbergen. Es erlaubt uns auch das Dazumischen weiterer nicht zugeordneter Farben zu einem bestehendem Commitment. Das Ergebnis ist ein neues Commitment, das den gleichen Inhalt hat wie das ursprüngliche (die zugeordnete Farbe hat sich ja nicht geändert), aber anders aussieht. Das Dazumischen lässt sich überprüfen. Wenn man weiß, welche nicht zugeordneten Farben dem ursprünglichen Commitment hinzugemischt wurden, kann man durch Nachmischen nachprüfen, dass beide Commitments den gleichen Inhalt haben. Um das neue Commitment zu öffnen, muss man lediglich der Liste der nicht zugeordneten Farben die dazugemischte Farbe hinzufügen. Diese zusätzliche Eigenschaft spielt eine zentrale Rolle für das zweiten Werkzeug der Kryptologie, das wir hier kennen lernen.

Zero-Knowledge-Beweise
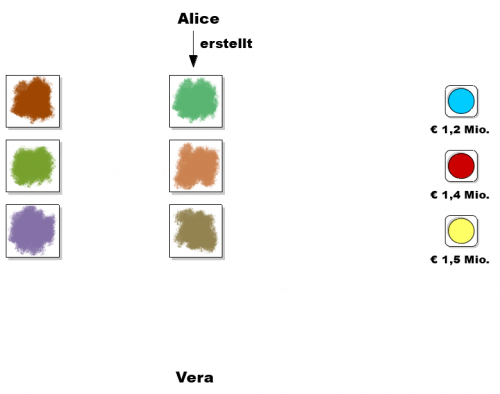
Vera ist eine junge und aufstrebende Journalistin und möchte über den Bau des neuen Rathauses berichten und vor allem die Vergabe transparent machen. Dazu fragt sie Alice nach den Geboten, die die Firmen abgegeben haben. Um die Interessen der Bieter zu schützen kann Alice allerdings nicht verraten, welcher Bieter welches Gebot abgegeben hat. Sie hat jedoch von den Bietern die Erlaubnis bekommen, die Liste der abgegebenen Gebote zu veröffentlichen, wenn nicht ersichtlich ist, wer welches Gebot abgegeben hat. Vera nimmt die Liste der Commitments, die im Rahmen des Bieterverfahrens veröffentlicht wurden, und die Liste der Gebote dankend entgegen, zusammen mit der Versicherung von Alice, dass jedes Gebot in einem der Commitments enthalten sei.

Als gute Journalistin glaubt Vera diese Aussage nicht einfach sondern überprüft sie. Alice darf jedoch die Zuordnung zwischen Commitment und Gebot nicht verraten, denn sonst wäre klar, welcher Bieter welches Gebot abgegeben hat. Die speziellen Commitments, die die Bieter bei dem Bieterverfahren für ihre Gebote verwendet haben, erlauben aber einen sehr eleganten Ausweg, nämlich die Verwendung eines Zero-Knowledge-Beweises.

Bevor wir anfangen, müssen wir noch kurz eine Kleinigkeit klären. Alice möchte Vera "beweisen", dass die Inhalte der Liste der Commitments mit der Liste der Gebote übereinstimmt. Da stellt sich die Frage, was ist hier mit einem "Beweis" gemeint. Juristen und Mathematiker beispielsweise benutzen den Begriff, haben aber etwas unterschiedliche Vorstellungen davon, was ein Beweis genau ist. Gemein hat jedoch allen die Vorstellung, dass ein Beweis etwas ist, was mich überzeugt. Warum ein Zero-Knowledge-Beweis überzeugend ist sehen wir gleich. Zero-Knowledge-Beweise sind interaktive Beweis-Systeme mit ein paar kontraintuitiven Eigenschaften, die ich erstaunlich finde und die wir uns hier näher anschauen wollen.

Zunächst ist ein Zero-Knowledge-Beweis nicht einfach ein statischer Text, sondern ein Gespräch zwischen dem Beweiser, hier Alice, und einem Verifizierer, hier Vera, das über mehrere Runden geht. Alice möchte Vera überzeugen, dass ihre Behauptung korrekt ist und dass Alice ein bestimmtes Geheimnis kennt, aus dem sich die Behauptung direkt ergibt. Zu Zero-Knowledge-Beweisen hat Matthew Green eine gute Erklärung auf Englisch geschrieben, die ein Zero-Knowledge-Beweissysten mit Graph-3-Färbbarkeit beschreibt. Das oben beschriebenen Commitment-Verfahren ermöglicht einen anderen Zero-Knowledge-Beweis, den wir im Folgenden betrachten.

Schauen wir uns zuerst genauer an, was Alice beweisen will: Öffentlich bekannt sind eine Liste von Commitments von den Bietern sowie eine (gleich lange) Liste von Zahlen. Alice behauptet, dass es sich dabei um die Gebote handelt, die in den Commitments enthalten sind. Die Listen sind nicht geordnet, das erste Commitment hat also nicht die erste Zahl als Inhalt. Tatsächlich soll geheim bleiben, welches Commitment welche Zahl als Inhalt hat. Alice Geheimnis besteht aus der Zuordnung zwischen Commitment und Inhalt sowie den Informationen zum Öffnen der Commitments, also den für das Mischen verwendeten Farben. Das Ziel des Zero-Knowledge-Beweises ist es, Vera davon zu überzeugen, dass Alices Behauptung stimmt, ohne dass sie irgendwelche Kenntnis über Alices Geheimnis erlangt.

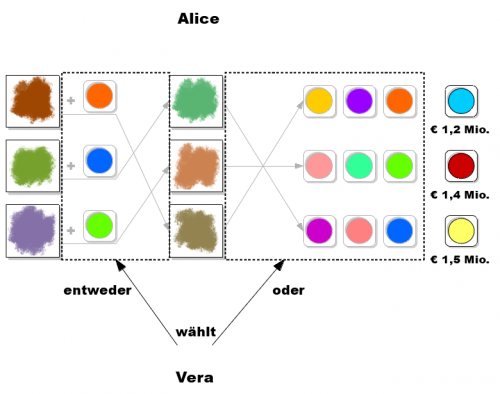
Um Vera zu überzeugen, erzeugt Alice zunächst neue Commitments und zeigt diese Vera. Dabei behauptet Alice, dass sie jedes der neuen Commitments durch Hinzumischen einer Farbe zu einem ursprünglichen Commitments erzeugt hat und die neuen Commitments damit den gleichen Inhalt haben wie die ursprünglichen. Anstatt die ursprünglichen Commitments direkt zu öffnen hat Alice mit der Erzeugung der neuen Commitments einen Zwischenschritt eingefügt und damit die zu beweisende Aussage in zwei Hälften zerlegt. Beide Hälften zusammen, also sowohl die Erzeugung der neuen Commitments aus den ursprünglichen als auch die Inhalte der neuen Commitments, verraten das Geheimnis von Alice. Jede Hälfte für sich aber ist wertlos.

Vera wählt, ob Alice die neuen Commitments öffnet oder ob sie ihr verrät, wie sie die neuen Commitments erzeugt hat. Wenn die Behauptung stimmt und Alice das Geheimnis kennt, kann sie beide Fragen beantworten. Kennt Alice das Geheimnis nicht, dann kann sie eine der beiden Fragen nicht beantworten. Damit hat Vera eine Chance von 50%, Alice zu erwischen, falls sie lügt. Vera allerdings empfindet eine 50%-ige Wahrscheinlichkeit, dass Alice sie anlügt, als zu hoch. Daher wiederholen Vera und Alice die Beweisschritte in einer neuen Runde. Alice erzeugt erneut eine Liste von neuen Commitments, und Vera wählt erneut, ob Alice die Erzeugung der neuen Commitments zeigt oder ob sie die neuen Commitments öffnet. Vera hat also wieder eine 50%-ige Chance, Alice beim Lügen zu erwischen. Bei zwei Wiederholungen liegt damit die Chance einen unehrlichen Beweiser zu erwischen schon bei 75%. Nach zehn Wiederholungen liegt die Chance bereits bei 99,9% Prozent. Durch weitere Wiederholungen lässt sich diese Chance beliebig nahe an 100% bringen. Vera kann die Beweisschritte so lange wiederholen, bis sie überzeugt ist, dass Alice das Geheimnis kennt und die fraglichen Inhalte tatsächlich in den Commitments enthalten sind.

Dieses Verfahren heißt Beweis, weil Vera am Ende überzeugt ist, dass die Behauptung stimmt. Aber warum nennt man es Zero-Knowledge? Ich habe behauptet, dass Vera als Verifizierer aus dem Gespräch mit Alice nicht mehr lernt als dass die Behauptung stimmt. Die Argumentation dafür ist ein bisschen abgefahren. Im Grunde dreht sich alles um die Frage, ob Vera ihren Lesern zusätzliche Informationen gibt, wenn sie das Gespräch mit Alice vollständig abdruckt, in dem Alice Vera beweist, dass die Inhalte der Liste der Commitment mit den später veröffentlichten Geboten übereinstimmt.

Betrachten wir dazu Walter, einen weiteren jungen und aufstrebenden Journalisten. Walter hat gehört, dass Vera über den Bau des neuen Rathauses berichtet und möchte ihr mit seiner Story zuvorkommen. Er nimmt sich aber nicht die Zeit, mit Alice zu sprechen und sich die Korrektheit ihrer Behauptung beweisen zu lassen. Stattdessen will sich Walter eine Unterhaltung mit Alice ausdenken, in der Alice ihn von der Korrektheit ihrer Behauptung überzeugt. Er stellt fest, dass dies ganz einfach ist. In der echten Unterhaltung zwischen Alice und Vera legt Alice zuerst eine Liste neuer Commitments vor, und Vera wählt dann, ob Alice die Entstehung der neuen Commitments aus den Originalen zeigt oder die neuen Commitments öffnet. Für seine ausgedachte Unterhaltung fängt Walter einfach mit der Frage an, die er als Verifizierer an die imaginäre Alice stellen will, und erzeugt dann die neuen Commitments entsprechend. Entscheidet er sich also für die Entstehung der neuen Commitments so erzeugt er einfach neue Commitments aus den alten. Entscheidet er sich hingegen für das Öffnen der neuen Commitments, so erzeugt er völlig neue Commitments, die die Gebote als Inhalt haben. Dann lässt Walter die imaginäre Alice die neuen Commitments präsentieren, stellt dann seine Frage und lässt die imaginäre Alice entsprechend antworten. Da seine Frage vorher feststand und Walter die neuen Commitments entsprechend erzeugt hat, kann er eine zur Frage passende Antwort angeben. Wie beim echten Beweis lässt sich dies beliebig wiederholen.

Eine von Walter erstellte Aufzeichnung einer Unterhaltung ist von der Aufzeichnung einer echten Unterhaltung nicht zu unterscheiden. Walter hat aber keine Ahnung, in welchem der Commitments, die die Bieter veröffentlicht haben, welches Gebot steckt. Also kann in der ausgedachten Aufzeichnung der Unterhaltung also auch keine Information darüber enthalten sein. Und wenn es nicht möglich ist, die Aufzeichnung einer ausgedachten Unterhaltung von einer echten zu unterscheiden, so ist auch in der echten Aufzeichnung keine Information über das Geheimnis enthalten. Die Aufzeichnung enthält alles, was der Verifizierer (in unserem Beispiel Vera) sieht, und daraus folgt, dass der Verifizierer zwar von der Korrektheit der Behauptung überzeugt ist, aber keine Informationen über das Geheimnis erhält.

An dieser Stelle muss ich zugeben, dass mir erst bei der Erstellung der Bilder aufgefallen ist, dass für den Zero-Knowledge-Beweis das Beispiel mit den Farben nicht funktioniert. Mich würde wirklich brennend interessieren, wer von den Lesern es ebenfalls gemerkt hat. Da ich aber leider kein besseres verständliches Beispiel für die Commitments habe, möchte ich hier stattdessen diskutieren, warum es nicht funktioniert, denn bekanntlich lernt man aus Fehlern ja am meisten (und es müssen nicht immer die eigenen sein). Schauen wir uns noch einmal genau an, wie die Antwort von Alice aussieht, wenn sich Vera für das Öffnen der neuen Commitments entscheidet. Alice nennt für jedes Commitment die zugeordnete Farbe sowie die Liste der nicht zugeordneten Farben, mit denen das Commitment erstellt wurde. Vera weiß jetzt aber, dass eine der nicht zugeordneten Farben nachträglich hinzugemischt wurde, um das neue Commitment zu erstellen. Sie kann einfach das Commitment nachmischen und dabei nacheinander jeweils eine der nicht zugeordneten Farben weglassen, bis sie eines der ursprünglichen Commitments erhält. Damit ist der Beweis auch kein Zero-Knowledge-Beweis, denn natürlich funktioniert dies nicht bei einer Aufzeichnung, die sich Walter ausgedacht hat.

Mein erster Gedanke war, dass sich dieses Problem lösen lässt, indem beim Öffnen eines Commitments nicht die Liste der nicht zugeordneten Farben genannt wird, sondern lediglich das Ergebnis, wenn man alle nicht zugeordneten Farben zusammenmischt. Dann könnte man nicht mehr durch Ausprobieren und Weglassen einzelner Farben beim Nachmischen ein ursprüngliches Commitment erhalten. Das würde zwar die Zero-Knowledge-Eigenschaft des Beweises retten, aber leider wäre damit das Commitment nicht mehr verbindlich. Denn beim Öffnen ließe sich nicht mehr überprüfen, ob Bob tatsächlich nur genau eine zugeordnete Farbe verwendet hat. Dies ist aber die Voraussetzung für die Verbindlichkeit des Commitments. Kleine Änderungen am Verfahren haben also drastische Auswirkungen auf die Sicherheit des Verfahrens. Dies ist bei vielen Verfahren der Kryptologie der Fall, und das macht die IT-Sicherheit so schwierig.

Ich habe bereits weiter oben gesagt, dass die mathematischen Strukturen, die für diese Commitments verwendet werden, die Eigenschaften besitzen, die ich für die Farben in unserem Beispiel postuliert habe. Hier tritt auch das beschriebene Problem mit dem Zero-Knowledge-Beweis nicht auf. Tatsächlich sind die realen Commitments bedingungslos verbergend (daher heißt das Verfahren "unconditionally hiding"), nicht einmal jemand mit unbegrenzter Rechenleistung oder einem Quantencomputer kann einem Commitment ansehen, was der Inhalt ist.

Wir haben gesehen, woher der Begriff Zero-Knowledge-Beweis kommt und warum ich es ein interaktives Beweis-System genannt habe.
Eine mögliche Anwendung für Zero-Knowledge-Beweise ist die Authentifizierung. In den meisten Fällen authentifiziert sich ein Computer (Client) bei einem anderen (Server), indem der Client ein Passwort an den Server übersendet und der Server dies mit einem gespeicherten Wert abgleicht. Verschlüsselung schützt das Passwort bei der Übertragung und eine Hashfunktion verhindert, dass der Server das Passwort direkt speichert (um es vor Diebstahl zu schützen). Diese Schutzmaßnahmen werden hinfällig, wenn statt eines Passworts ein Zero-Knowledge-Beweis verwendet wird. Der Client beweist dem Server, dass er ein bestimmtes Passwort kennt, und durch den Zero-Knowledge-Beweis ist sicher gestellt, dass niemand (nicht einmal der Server) das Geheimnis erfährt.

Die Authentifizierung ist aber bei Weitem nicht die einzige Anwendungsmöglichkeit für Zero-Knowledge-Beweise. Tatsächlich sind sie ein mächtiges Werkzeug der Kryptologie und ermöglichen viele weitere erstaunliche Leistungen. Zusammen mit dem Commitment-Verfahren, das wir oben kennen gelernt haben, bilden die hier beschriebenen, speziellen Zero-Knowledge-Beweise beispielsweise die Grundbausteine von Bingo Voting. Bingo Voting ist ein Wahlverfahren, bei dem der Wähler seine Stimme an einem Wahlcomputer abgibt und einen Beleg erhält. Mit diesem Beleg kann der Wähler kontrollieren, dass seine Stimme korrekt gezählt wurde, sogar wenn der Wahlcomputer manipuliert wurde und versucht, die Wahl zu verfälschen. Wer mehr zu Bingo Voting erfahren möchte, dem empfehle ich die Wikipedia-Seite von Bingo Voting als Einstieg.