Raumfahrt ist kompliziert und teuer. Ein bisschen billiger wird sie durch den Einsatz des Swing-By-Manövers. Billiger, aber nicht weniger kompliziert. Denn bei einem Swing-By nutzt man die Energie der Planeten, um die Raumsonde anzutreiben und ihre Bahn zu ändern. Das kostet nichts, abgesehen von jeder Menge mathematischer Berechnungen. Das Prinzip dahinter ist aber nicht allzu schwer zu verstehen und Thema der heutigen Folge der Sternengeschichten.
Und wie immer gibt es weiter unten eine Transkription des Podcasts.
Die Folge könnt ihr euch hier direkt als YouTube-Video ansehen oder direkt runterladen.
Den Podcast könnt ihr unter
abonnieren beziehungsweise auch bei Bitlove via Torrent beziehen.
Am einfachsten ist es, wenn ihr euch die „Sternengeschichten-App“ fürs Handy runterladet und den Podcast damit anhört.
Die Sternengeschichten gibts natürlich auch bei iTunes (wo ich mich immer über Rezensionen und Bewertungen freue) und alle Infos und Links zu den vergangenen Folgen findet ihr unter https://www.sternengeschichten.org.
Und natürlich gibt es die Sternengeschichten auch bei Facebook und bei Twitter.
Transkription
Sternengeschichten Folge 207: Swing-by – Raumfahrt mit der Kraft der Planeten
Wenn wir Raumsonden zu anderen Himmelskörpern in unserem Sonnensystem schicken, dann nutzen wir dabei fast immer sogenannte „Swing-by“-Manöver. Dabei handelt es sich um eine äußerst elegante Methode, Geschwindigkeit und Bahn von Flugkörpern zu verändern die keinen oder nur sehr wenig Treibstoff benötigt. Denn der Treibstoff ist ja normalerweise das, was die Raumfahrt so kompliziert macht.
Alle Raumsonden müssen mit Raketen von der Oberfläche der Erde ins Weltall gebracht werden. Dafür muss das Gravitationsfeld unseres Planeten überwunden werden und das braucht Energie. Mit dem Verlassen des Schwerefelds der Erde ist es aber noch lange nicht getan. Wenn die Raumsonde einen anderen Himmelskörper erreichen will, dann braucht man dazu ebenfalls Treibstoff. Wie viel, das hängt von den konkreten Gegebenheiten ab. Manchmal soll eine Raumsonde ein sehr fernes Ziel erreichen. Im Prinzip ist das eigentlich kein Problem. Das erste Newtonsche Axiom, das grundlegende Prinzip der klassischen Physik besagt, dass sich ein Körper der sich mit einer gewissen Geschwindigkeit bewegt auch weiterhin immer mit dieser Geschwindigkeit bewegen wird, solange keine äußere Kraft auf ihn einwirkt. Auf der Erde sind es Reibungskräfte mit dem Untergrund oder der Luft die dafür sorgen, dass ein bewegter Körper immer langsamer wird und irgendwann still steht. Im All gibt es das aber nicht und eine Raumsonde, die die Erde mit einer gewissen Geschwindigkeit verlässt wird sich mit dieser Geschwindigkeit auch weiterhin bewegen. Und irgendwann an ihrem Ziel ankommen.
Das „irgendwann“ ist das Problem. Denn man möchte das Ziel ja möglichst schnell erreichen – und die Distanzen im Sonnensystem sind enorm groß. Um die riesigen Entfernungen in halbwegs überschaubaren Zeiträumen überwinden zu können müssen die Raumsonden ausreichend schnell sein. Das kann man erreichen, in dem man sie schon möglichst schnell von der Erde aus in den Weltraum schießt. Dann braucht man aber auch entsprechend schnelle Raketen, die entsprechend viel Treibstoff haben müssen und entsprechend groß und teuer werden. Oder aber man stattet die Raumsonde selbst mit einem Antrieb und Treibstoff aus, damit sie aus eigener Kraft schneller werden kann. Je schneller sie werden soll, desto mehr Treibstoff benötigt man und desto schwerer wird sie. Und je mehr Masse sie hat, desto größer muss wiederum die Rakete sein und desto mehr Treibstoff braucht auch sie.
Eine Raumsonde die sich einfach ohne Antrieb durchs All bewegt kann auch nicht gesteuert werden. Jede Veränderung ihrer Bahn muss durch eine Kraft ausgelöst werden; und dafür braucht es Triebwerke die wiederum Treibstoff benötigen. Wenn man alles ganz exakt berechnet und die Sonde im richtigen Moment und in der richtigen Richtung mit der richtigen Geschwindigkeit ins All schießt, dann kann sie ihr Ziel auch ohne Kurskorrekturen erreichen. Aber so exakt laufen die Dinge selten, kleine Korrekturen sind fast immer nötig. Und oft auch größere, wenn man zum Beispiel einen Himmelskörper erreichen will, dessen Bahn gegenüber der Erdbahn stark geneigt ist. Dann muss man auch die Raumsonde auf eine ebenso geneigte Umlaufbahn bringen, was wiederum einen Antrieb und Treibstoff benötigt.
Und wenn die Raumsonde dann am Ziel angekommen ist? Dann will man ja im Allgemeinen nicht einfach daran vorbeifliegen sondern in eine Umlaufbahn um den Himmelskörper einschwenken oder vielleicht sogar landen. Und auch das braucht wieder Treibstoff. Ohne Treibstoff scheint es also nicht zu gehen.
Es sei denn, man nutzt das Swing-By-Manöver! Das Prinzip dahinter ist eigentlich recht simpel. Newtons Axiom besagt ja nur, dass eine Kraft nötig ist, um die Bewegung eines Objekts zu verändern. Aber nicht, dass diese Kraft durch ein Triebwerk verursacht werden muss. Es gibt auch noch andere Kräfte, die man nutzen kann. Zum Beispiel die Gravitationskraft der Planeten in unserem Sonnensystem. Genau so wie die Erde die Rakete und Raumsonde beim Start anzieht und den Weg in den Weltraum so aufwendig macht, ziehen auch die anderen Planeten die Raumsonde an, wenn sie deren Gravitationsfeld ausreichend nahe kommt. Wenn sie beispielsweise sehr nahe am Jupiter vorbei fliegt, wird sie das nicht einfach unbeeinflusst tun – ihre Bahn wird verändert werden. Aus Sicht des Jupiters findet dabei tatsächlich nur eine Ablenkung statt. Die Raumsonde fliegt nach dem Vorbeiflug in eine andere Richtung als vorher, aber immer noch mit der gleichen Geschwindigkeit. Der Jupiter selbst steht aber nicht still sondern bewegt sich selbst um die Sonne. Und wenn man das ganze aus der Sicht der Sonne betrachtet, hat sich nach dem Vorbeiflug am Planeten nicht nur die Flugrichtung der Sonde verändert sondern auch ihre Geschwindigkeit.
Man kann das mit einem Beispiel von der Erde vergleichen. Stellen wir uns einen Zug vor, der auf seinen Gleisen mit einer Geschwindigkeit von 100 km/h fährt. Neben den Gleisen steht eine Person und wirft einen Ball in Richtung des Zuges (kurzer Hinweis: Das ist nur ein Beispiel! Bitte nicht nachmachen!). Wenn der Ball des Werfers eine Geschwindigkeit von 20 km/h hat, dann wird der Lokführer diesen Ball mit einer Geschwindigkeit von 120 km/h auf sich zu kommen sehen. Wenn der Ball dann auf das Führerhaus der Lokomotive trifft, prallt er dort ab und er ändert seine Richtung. Nach dem Aufprall wird er sich aber schneller bewegen als vorher. Zu den 20 km/h die er von Anfang an hatte kommen nun noch die 100 km/h, mit denen er vom Zug zusätzlich „angeschoben“ wird. Er bewegt sich nun also mit 120 km/h. Aus Sicht des sich bewegenden Lokführers hat sich nur die Richtung geändert; die Geschwindigkeit des Balls war vor und nach dem Aufprall identisch. Aus Sicht des Werfers wurde der Ball aber auch von 20 km/h auf 220 km/h beschleunigt.
Genau so läuft es im Prinzip auch bei einem Swing-By im Weltall. Nur ist es eben hier kein Zug sondern ein Planet, der die Kraft ausübt. Und die Kraft wird nicht durch einen mechanischen Akt übertragen sondern durch die gravitative Wechselwirkung. Die Geschwindigkeit kann dabei aber nicht nur größer werden sondern auch kleiner, je nachdem ob die Sonde die Umlaufbahn des Planeten hinter oder vor dem Planeten überquert. Die Energie, die für die Veränderung von Bahn und Geschwindigkeit verantwortlich ist kommt dabei natürlich nicht aus dem Nichts. Das, was die Raumsonde an Geschwindigkeit dazu gewinnt verliert der Jupiter (und umgekehrt). Aber da die Masse der Raumsonde im Vergleich zur Masse des großen Planeten verschwindend gering ist, sind auch die Auswirkungen auf die Umlaufbahn des Jupiters verschwindend gering.
Mit einem Swing-By kann man also nicht nur die Bahn eines Himmelskörpers verändern sondern auch seine Geschwindigkeit (obwohl jede Geschwindigkeitsänderung im Weltall sowieso auch immer einer Änderung der Umlaufbahn entspricht). Und das alles, ohne Treibstoff zu benötigen – man nutzt die Bewegungsenergie der Planeten!
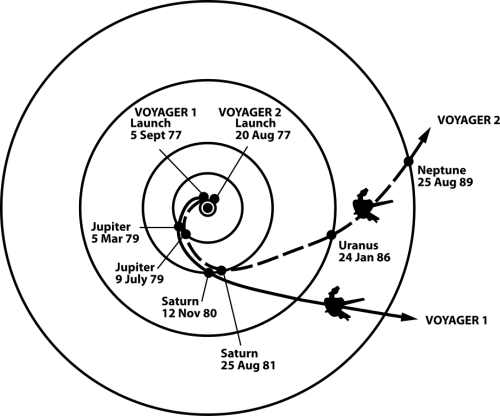
Das man auf diese Art und Weise durch das Sonnensystem fliegen kann, hat der amerikanische Mathematiker Michael Minovitch im Jahr 1961 entdeckt, als er noch ein Student an der Universität von Kalifornien war. Er hatte damals einen Nebenjob am Jet Propulsion Laboratory wo man mit der Planung von Missionen zu den damals noch kaum erforschten Planeten unseres Sonnensystems beschäftigt war. Die große Stunde des Swing-Bys kam ein paar Jahre später als man mit den Planungen für die beiden Raumsonden Voyager 1 und 2 (über die ich in Folge 152 der Sternengeschichten mehr erzählt habe) begann. Ursprünglich sollten die beiden Sonden nur an Jupiter und Saturn vorbei fliegen. Dann aber entdeckte der Ingenieur Gary Flando, dass Jupiter, Saturn, Uranus und Neptun gegen Ende der 1970er Jahre gerade so im Sonnensystem angeordnet sein würden, dass man mit passenden Swing-By-Manövern die Bahnen der Voyager-Sonden so ändern konnte um nicht nur an zwei sondern an allen vier Planeten vorbei fliegen zu können. Nur so konnten sie im Rahmen des damaligen Budgets auf ihre große Tour durchs äußere Sonnensystem geschickt werden und all die großartigen Daten sammeln, die sie gesammelt haben.
Vorbeiflug von MESSENGER an der Erde
Swing-By-Manöver gehören heute zu den Standardmethoden in der interplanetaren Raumfahrt. Als die Raumsonde MESSENGER sich im Jahr 2004 zum Merkur aufmachte, war der Weg dorthin zwar nicht weit, aber sie musste ordentlich abbremsen um am Ende eine Umlaufbahn erreichen könnte. Das erreichte man mit passenden Vorbeiflügen an Erde, Venus und auch an Merkur bevor sie im Jahr 2011 schließlich langsam genug war. Als die Cassini-Sonde 1997 auf den Weg zum Saturn geschickt wurde, holte sie sich die dafür nötige Geschwindigkeit durch Vorbeiflüge an Venus, der Erde und Jupiter.
Die Entdeckung der Swing-By-Technik war in gewissen Sinn eine Einladung des Sonnensystems an uns, es noch intensiver zu erforschen als bisher. Die Himmelskörper, über die wir etwas herausfinden wollen, stellen uns selbst die dafür nötige Energie zur Verfügung. Wir haben die Einladung glücklicherweise nicht ignoriert – und nutzen die Möglichkeit die uns die Planeten mit ihrer Energie bieten hoffentlich auch in Zukunft ausgiebig!

Sie wirft den Ball also von vorn gegen die Fahrrichtung.
Oh?! Du hast doch nicht etwa 20+100 km/h gerechnet?!?
Im Falle eines voll elastischen Stoßes würde der Ball mit 120km/h abprallen und sich so mit 220 km/h relativ zu den Gleisen herauskommen. Ansonsten können je nach Verlust an kinetischer Energie auch geringere Geschwindigkeiten herauskommen.
@Uma: „Oh?! Du hast doch nicht etwa 20+100 km/h gerechnet?!?“
Doch. Weil der Ball 20km/h drauf an und der Zug 100 km/h.
Für die Relativgeschwindigkeit vor dem Stoß ist das richtig, aber die Geschwindigkeit nach dem Stoß kann man so definitiv nicht ausrechnen.
https://de.wikipedia.org/wiki/Sto%C3%9F_(Physik)
@UMa
Irgendwie bin ich froh, dass Florian nicht die Kollisionswahrscheinlichkeiten erdnaher Asteroiden mit Planeten des inneren Sonnensystems behandelt 😉
Spaß beiseite. Ich nehme an, dass Florian ziemlich eingeteilt ist und sehr wenig Zeit hat.
Auch wenn einem das Bauchgefühl sagt, das passt, so sollte man es doch einmal durchrechnen 😉
Der Zug sei die Wand. Beim elastischen Stoß des Balls mit der Wand ändert die Geschwindigkeit des Balls seine Richtung.
Nachdem die Wand sprich unser Zug mit 100 km/h unterwegs ist, hat der Ball für den Werfer eine Geschwindigkeit von 120 km/h + 100 km/h = 220 km/h
@Karl-Heinz: „achdem die Wand sprich unser Zug mit 100 km/h unterwegs ist, hat der Ball für den Werfer eine Geschwindigkeit von 120 km/h + 100 km/h = 220 km/h“
Ich hab eigentlich nur diese Analogie hier übersetzt: https://solarsystem.nasa.gov/basics/grav/primer.php Wo genau hab ich Fehler gemacht?
Also ich finde das furchtbar! Diese kurzfristige Denkweise! Da werden Planeten ohne nachzudenken abgebremst oder beschleunigt, nur damit wir Menschen es uns wieder mal einfach machen können! Wenn dann mal der Jupiter so stark abgebremst wurde, dass er in die Sonne stürzt – dann jammern wieder alle!
xkcd hat eine interessante Diskusion, ob Jupiter mit Swingbys gestoppt werden kann.
https://what-if.xkcd.com/146/
@Florian der Zug kommt nur mit 50 mp/h
Also 2*50+30 wie Karlheinz schreibt.
@Florian
Ball (30+50) + Zug(50) = 130 mp/h
Lg Karl-Heinz
@Florian
Dein Zug hätte mit 50 km/h fahren müssen (so wie der in dem von Dir verlinkten Artikel mit 50 mph), dann hätte es gestimmt. Aus der Sicht eines mit 100 km fahrenden Zugs kommt ihm der Ball mit 120 km/h entgegen und wird ihn mit 120 km/h Relativgeschwindigkeit wieder in die Fahrtrichtung verlassen. Aus der Sicht eines ruhenden Beobachters sind die 120 km/h Relativgeschwindigkeit in Fahrtrichtung dann 100 km/h + 120 km/h = 220 km/h absolut.
@Alderamin: „Aus der Sicht eines mit 100 km fahrenden Zugs kommt ihm der Ball mit 120 km/h entgegen und wird ihn mit 120 km/h Relativgeschwindigkeit wieder in die Fahrtrichtung verlassen. Aus der Sicht eines ruhenden Beobachters sind die 120 km/h Relativgeschwindigkeit in Fahrtrichtung dann 100 km/h + 120 km/h = 220 km/h absolut.“
Das wollte ich eigentlich auch sagen. Es ging ja darum, dass aus Sicht des Zuges der Ball immer gleich schnell ist und nur die Richtung ändert. Für den Zug ist der Ball immer 120km/h schnell. Für den Werfer ist der Ball zuerst 20 km/h schnell. Und danach? Hab ich mich verrechnet?
mph anstatt mp/h sorry
Allerdings muss ich jetzt mal wieder echt doof fragen.
Ein swing bei ist ja kein elasticher stoß. Und dass Beispiel irgentwie schlecht gewählt.
Somit würde Florians Rechnung ja eigentlich stimmen oder ?
Das könnte man missverstehen, als wäre eine Raumsonde ein Vehikel wie ein Auto, mit dem man schnell oder langsam fahren kann, um mehr oder weniger schnell ans Ziel zu kommen.
@tomtoo
Vom Prinzip her schon.
Nur das Prinzip
Einfallswinkel ist gleich Ausfallswinkel
kannst natürlich nicht übernehmen.
Daumen hoch für Florian, da Beispiel gut gewählt wurde. 🙂
@Florian
Du sagtest:
Nein, aus der Sicht des Werfers wurde der Ball von 20 km/h auf 220 km/h beschleunigt. (Aus der Sicht des Lokführers kehrte er nur die Richtung um).
100 km/h Lok + 120 km/h relativ zur Lok sind 220 km/ relativ zum Werfer.
@Florian
Ja …
Am besten mal Kaffeepause machen.
@Karl-Heinz: „Ja …“
Dann wäre es super, wenn du mir Fehler und die richtige Rechnung sagst.
Bzw. seh ich gerade, dass Alderamin das schon getan hat. Danke!
@Karl-Heinz
Ok vielen Dank.
Ich dachte der Planet könnte max. die Eigengeschwindigkeit mitgeben.
Ich bin verwirrt.
@Alderamin
Erwischt …
Der Ball wurde aus Sicht des Werfers von -20 km/h auf 220 km/h beschleunigt.
20 km/h sind 20 km/h
@Karl Heinz
Doch, ihm Ruhesystem des Planeten wird eine Hyperbel geflogen, bei der durchaus Einfallswinkel = Ausfallswinkel gilt.
Die Änderung der Richtung ist sogar wesentlich: wenn der Planet einfach geradlinig überholt würde, dann wäre die Geschwindigkeit der Raumsonde relativ wie absolut nachher nicht größer als vorher, weil die Schwerkraft des Planeten ihn aus seiner Sicht um den gleichen absoluten Wert beim Anflug beschleunigt, wie sie ihn beim Wegflug wieder abbremst, und ohne Änderung der Richtung wäre das +/- wieder die gleiche Geschwindigkeit. Wie es mit Richtungsänderung vektoriell dann doch funktioniert, zeigen sehr anschaulich die Bildchen im zugehörigen Wikipedia-Artikel.
@Alderamin
Danke für den Link.
Ich meinte ja nur, dass die Richtungsänderung bei Swing-By doch ein bisschen komplizierter zu berechnen ist, als beim elastischen Stoß (Winkeln zum Lot oder Horizont).
@Florian: Schon besser, aber ich denke der Abschnitt
ist immer noch nicht richtig.
Dies Sätze danach stimmen jetzt, zumindest für einen voll elastischen Abprall.
@Uma: Was GENAU stimmt denn noch nicht? Die Mathematik? Oder die Physik? Natürlich ist das was beim Zug passiert KEIN Swing by. Es soll nur ein Beispiel für die Tatsache sein, das aus dem einen Blickwinkel nur eine Richtungsänderung stattfindet, aus dem anderen aber auch eine Geschwindigkeitsänderung.
Vielleicht sollte man auch erwähnen, dass die korrekte Geschwindigkeitsänderung des Balls Δv= (Δvx, Δvy, Δvz)
220 km/h – (-20 km/h) = 240 km/h beträgt, da ja beim Wurf des Balls auf den Zug, genau die entgegengesetzte Richtung vorherrscht im Gegensatz zur Richtung, wie der Ball zurück kommt.
mal was anderes, Ihr redet immer vom Jupiter, und tatsächlich wird er auch gerne zum swing-by genommen. Aber die Masse des Planeten ist doch egal, solange sie nur sehr groß im Verhältnis zur Raumsonde. Wichtig ist doch nur die Relativgeschwindigkeit zur Sonne, und die ist beim Merkur am Größten. Wenn man also auf hohe Geschwindigkeiten kommen will, z.B um das Sonnensystem zu verlassen, beschleunigt man am Besten am Merkur.
@pane
So einfach ist das nicht. Wenn eine Sonde zum Merkur runterfliegt (runter, weil der tiefer im Gravitationstrichter der Sonne sitzt als die Erde), wird die Sonde von der Gravitation der Sonne immens beschleunigt (diese Energie geht ihr beim Entfernen von der Sonne dann wieder verloren). Das heißt, dass sie Merkur mit hoher Geschwindigkeit passiert. Dann ist aber auch die Hyperbel nur minimal gewinkelt und der erzielbare Geschwindigkeitsvorteil nur klein.
Besser ist ein Vorbeiflug mit geringer Geschwindigkeit an einem Planeten, dann wird die Bahn stärker umgelenkt. Wenn man aus dem Sonnensystem heraus will, sollte man daher einen äußeren Planeten verwenden, wo die Startgeschwindigkeit schon von der Gravitation der Sonne stark verringert wurde.
Und je größer der Planet ist, desto mehr kann er eine Bahn bei einer gegebenen Geschwindigkeit ablenken. Daher ist Jupiter die beste Wahl.
@pane
Wenn Du Lust hast zum Querlesen …
„Swing-by-Manöver – Was steckt dahinter? – Spektrum der Wissenschaft“
http://www.spektrum.de/pdf/suw-2003-12-s022-pdf/833979?file
@Uma
Ich finde Florians Argumentation auch nicht ganz stimmig.
@alle: Wie sieht es denn mit dem Beispiel auf der verlinkten NASA Seite aus? Ist das auch falsch? Eigentlich hab ich das nur übersetzt…
Aus Sicht des Werfers wurde der Ball aber auch von 20 km/h auf 220 km/h beschleunigt.
Ach ja wirklich? … wenn schon denn schon
Beschleunigung hat immer schon was mit Geschwindigkeitsänderung zu tun.
Daher folg: Aus Sicht des Werfers wurde der Ball aber auch von -20 km/h (minus 20 km/h) auf 220 km/h beschleunigt.
@Florian: Ich weiß nicht ob es ein Physik-, Denk-, Schreib- oder Rechenfehler von dir ist. Rein formal sieht es so aus, als hättest du die Physik des Stoßvorgangs nicht verstanden, was ich aber wegen deines Studiums für unwahrscheinlich halte. Vielleicht hast du ja auch nur beim Überarbeiten Teilsätze falsch zusammengefasst und meinst es ganz anders, als es da steht. (Das passiert mir immer wieder).
In dem besagten Abschnitt sieht es so aus, als ob du so argumentierst:
Der Ball bewegt sich mit 20km/h (relativ zu den Gleisen), der Zug bewegt sich mit 100km/h (relativ zu den Gleisen). Um jetzt die neue Geschwindigkeit des Balls (relativ zu den Gleisen) nach dem Aufprall zu bestimmen, braucht man nur die Geschwindigkeit des Balls und des Zugs zu addieren, also 20km/h+100km/h=120km/h ist die Geschwindigkeit des Balls (relativ zu den Gleisen) nach dem Stoß mit dem Zug.
Dies ist offensichtlich falsch, so kann man die neue Geschwindigkeit des Balls nicht bestimmen, in dem man einfach die beiden Geschwindigkeiten addiert.
Aber; genau so interpretiere ich deine Sätze:
Am besten die zwei Sätze streichen und schon passt es 🙂
@pane: Es kommt auf die Fluchtgeschwindigkeit des Planeten an. Wenn die Geschwindigkeit der Sonde gegenüber der Fluchtgeschwindigkeit des Planeten zu groß ist, ist der Winkel in dem die Sonde abgelenkt wird und damit auch die Geschwindigkeitsänderung zu klein. An einem Asteroiden, auch wenn er viel schwerer als die Sonde ist, fliegt die schnelle Sonde nahezu gerade vorbei, ohne Richtung oder Geschwindigkeit nennenswert zu ändern.
Das ist einer der Fälle, wo ein bisschen mehr Formalismus sehr zur Klarheit beiträgt. Wir haben hier zwei Koordinatensysteme, nennen wir sie W (Werfer) und L (Lokomotive). Vor dem Stoß:
In W-Koordinaten:
Ball bewegt sich mit -20
Lokomotive bewegt sich mit +100
In L-Koordinaten:
Ball bewegt sich mit -120
Lokomotive bewegt sich (per definitionem) mit 0
Werfer bewegt sich mit -100
Nach dem Stoß:
In L-Koordinaten: Ball bewegt sich mit +120 (elastischer Stoß)
In W-Koordinaten: Ball bewegt sich mit 220
Das ist wohl genau das, was Florian uns mit diesem Absatz sagen will, aber vielleicht geht nicht immer klar hervor, welches Koordinatensystem gemeint ist.
@Lercherl
Schön formuliert (smiley).
@Florian
So weit ich erkennen konnte argumentiert man auf der NASA-Seite vor dem Stoß zuerst mit der Relativgeschwindigkeit zwisch Zug und Ball (50 mph + 30 mph) und nach dem elastischen Stoß wie beim elastischen Stoß üblich Vorzeichenwechsel von (50 mph + 30 mph).
Da aber die Wand sprich der Zug nicht still steht muss zusätzlich noch die Geschwindigkeit vom Zug (50 mph) aufaddiert werden.
(50 mph + 30 mph) + (50 mph vom Zug).
Wenn mans so sieht ist es natürlich korrekt.
Ich bevorzuge aber den Impulssatz (Impuls bleibt konstant), da hier eindeutig festgelegt ist, wie man rechnet und man das Gehirn ausschalten kann, wenn man weiß, wie man die Gleichungen aufstellen muss.
Und ich glaub natürlich auch der Energieerhaltunssatz wird benötigt.
Ich hab das Beispiel leider auch nicht nach der Methode gerechnet.
Lieber Florian,
es war zwar ein interessanter und unterhaltender Artikel, eine wirkliche Erklärung für eine Geschwindigkeitserhöhung hast Du nicht gegeben, oder siem ist mehr verdeckt geblieben, denn Dein Beispiel mit dem Zug taugt wegen eines mechnischen Stoßes überhaupt nicht für diesen Fall.
Als ich die Bilder der Voyager Sonden live im Fernsehen sah, wurde auch schon von „Swing by“ erzählt, ich verstand es als Kind aber nicht einmal im Ansatz. Heute versuche ich es mir damit zu erklären, dass die relative Gewindigkeit der Objekte sehr entscheidend für den Effekt ist.
Stellen wir und einen feststehenden Körper vor und eine Sonde fliegt auf ihn zu, dann wird sie beschleunigt. Sobald sie sich von ihm entfernt, aber im selben Maße verzögert. Der zeitliche Gewinn einer Reise liegt nur daran, dann man temporär schneller wird, dafür aber in der Regel auch einen längeren Weg zurück legen muss. Kann helfen, muss aber nicht
Bewegt sich der Planet aber von einem Objekt weg, sieht es anders aus. Über die Schwerkraft wirkt eine Kraft zwischen Palnet und Sonde. Die übertragene Energie ergibt sich aus Kraft mal Weg. Die Zeit spielt dabei überhaupt keine Rolle, nur die Stärke des Gravitationsfeldes, die in dritter Potenz vom Abstand abhängig ist.
Fliege ich auf einen Planeten zu und dieser bewegt sich von mir weg, dann wirkt seine Schwerkraft, oder genauer das Integral aus Schwerkraft mal Weg, auf einer sehr langen Strecke und ich werde hoch beschleunigt. Umkreist man nach Annäherung den Planeten um idealerweise 180° fliegt man mit höherer Geschwindigkeit entgegengesetzt zum Planeten wieder weg. Der Unterschied der Relativgeschwindigkeit beträgt die doppelte Planetengeschwindigkeit. Die Erde bewegt sich um die Sonne mit ca. 53.000km pro Stunde, um nur eine Größenordnung zu bekommen. So schnell wird keine Rakete relativ zur Erde.
Darum verändert sich die Wirkung der Gravitation, also das Intergral. Weil sich der Planet von der Sonde mit hoher Geschwindigkeit entfernt, sinkt die wirkende Kraft zwischen Sonde uznd Planet sehr schnell ab. Integriert man beide Fälle, Annäherung und Entfernung von einem Planeten mit Relativgeschwindigkeit, kommen erheblich unterschiedliche Energien zusammen, die die Sonde in Summe beschleunigt, oder je nach Anflugrichtung verzögert.
Ist meine laienhafte Vorstellung verständlich und korrekt? Eine kurze Antwort würde mir helfen, damit ich dieses Problem, welches seit 40 Jahren immer wieder in meinem Kopf geistert, endlich zur Seite legen kann. 🙂
Eine Erklärung zum Beispiel mit dem Zug.
Annahme: Ball 20km/h, Zug -100km/h
Ich bin gerade verwirrt, was hier geschrieben wird, Stellen wir uns den Fall vor, dass ein Ball direkt mit 20km/h auf einen Zug geworfen wird. Der Ball hätte für den Betrachter die Geschwindigkeit 20km/h. Dann prallt er auf den Zug.
Unterscheiden müssen wir die beiden Grenzfälle elastischer Stoß oder plastischer Stoß. Plastisch würde er mit der Geschwindigkeit des Zuges mitgenommen werden, sich also mit -100km/h auf den Betrachter zubewegen. Es gäbe eine Geschwindigkeitsänderung aus Sicht des Betrachters von 120km/h.
Im elastischen Fall würde der Ball wieder mit 20km/h relativ zum Zug abprallen, Er käme das auf die Geschwindigkeit -120km/h. Relativ gäbe es zum Betrachter eine Änderung um 140km/h.
Das Beispiel passt darum durchaus als Analogie für Swing by, denn das Gesamtverhalten der Sonde ist ebenso abhängig von bestimmten Kennwerten. Was beim Stoß elastisch oder plastisch ist, liegt im Falle von Sonde um Planet an der Relativgeschwindigkeit und der Schwerkraft des Planeten.
Beispiel 1:
System: ruhender Planet, ruhende Sonde, unendlich weit entfernt, keine weiteren Objekte.
Durch die Schwerkraft wird die Sonde angezogen und auf eine maximale Geschwindigkeit beschleunigt. Bei der Erde sind es glaube ich 40.000 km/h. Man könnte die Erde dann aber nicht umkreisen, denn die maximale Geschwindigkeit für eine gebundene Umkreisung irgendwo um 28.800km/h liegt, wenn ich mich an Querfurth von Hoimar mit Ditschnitt korrekt erinnere.
Bewegt sich die Erde aber von der Sonde weg, wird die Sonde mit der Zeit erheblich schneller als 40.000 km/h. Die max. Grenzgeschwindigkeit ist dabei abhängig von der Entfernung von Sonde zu Planet. Ist der Planet zu schnell, wird die Sonde niemals ankommen. Ist sie aber näher dran, durchaus. Müsste man mal in Ruhe das Optimunm auf Sondenposition und Planetengeschwindigkeit ausrechnen, habe ich jetzt keine Lust zu.
Da für ein Swing by Manöver aber eine Flugrichtungsumkehr entscheidend ist, ist die Masse des Planeten sehr entscheidend. Um den Jupiter herum kann darum eine viel höhere Geschwindigkeit gewonnen werden, als um leichtere Planeten. Die Relativgeschwindigkeit des Planeten ist dabei nur eine Größe unter vielen und mitnichten bekommt eine Sonde die Relativgeschwindigkeit als Extrageschwindigkeit mit.
Meine gefühlte Meinung ….
@Rotkaeppchen_online
Stell dir eine Wand vor. Wird ein Ball auf die Wand geworfen so prallt er mit der Geschwindigkeit ab mit der er auf die Wand zugeworfen wurde. Das heisst Abprallgeschwindigkeit ist gleich gross wie Aufprallgeschwindigkeit. Was wird ein Radfahrer beobachten, wenn er sich von der Wand entfernt. Ist für den Radfahrer als Beobachter auch die Symmetrie, dass Abprallgeschwindigkeit gleich gross ist wie die Aufprallgeschwindigkeit gültig? Überleg mal.
Nein Karl-Heinz,
so einen idealisierten Ball gibt es in der Realität nicht, er verliert immer etwas Geschwindigkeit, mal mehr, mal weniger. Die physikalischen Grenzfälle sind elastischer Stoß und plastischer Stoß. Reale Objekte liegen immer irgendwo in der Mitte.
Nimm einen Ball in die Hand und las ihn runter fallen. Er kommt nie bis zur Ausgangshöhe zurück, es sei denn, der Boden bewegt sich auf ihn zu. 🙂
Und dann kommen wir im Übertragenen Sinn zum Swing by manöver
@Rotkaeppchen_online
Natürlich gibt es keinen 100% idealisierten Ball aber sehr wohl einen 99,99% idealisierten Ball. Bei der Modellbildung lässt man Dinge, die keine Rolle spielen einfach weg. Warum hast du nicht versucht die Überlegung nachzuvollziehen? Dann hättest Du gemerkt, wo dein Gedankenfehler liegt.
Muss leider weg, deshalb ganz kurze Formulierung
Die NASA argumentiert in ihrem Beispiel nicht mit Impuls-und Energieerhaltung, sondern mit der Erfahrung, die jeder von uns schon gemacht hat, dass beim Wurf eines Balls auf die Wand eine Symmetrie von Aufprall und Abprall-Geschwindigkeit besteht, d.h. beide Geschwindigkeiten sind vom Betrag her gleich groß. Das Problem dabei ist nur, dass die Symmetrie bezüglich Galilei-Transformation nicht invariant ist. Diese Symmetrie gilt nur, wenn die Wand als Bezugssystem gewählt wird. Wir das nicht beachtet, dann rechnet man falsch.
@Rotkäppchen_online #41
Nein, so funktioniert das nicht. Eine Ablenkung ist beim Swing-By wesentlich, sonst gibt es keine Geschwindigkeitszunahme. Die Beschleunigung und Abbremsung im Schwerefeld ist ja, wie Du selbst erkannt hast, symmetrisch im Ruhesystem des Planeten. Wenn die Sonde geradlinig den Planeten passieren würde, hätte er am Ende vektoriell die gleiche Relativgeschwindigkeit wie vorher. Wenn Du dem Vorgang eine konstante Geschwindigkeit des Planeten überlagerst, sind dann auch die Summen von Sonden- und Planetengeschwindigkeit vorher und nachher identisch.
Wesentlich für die Geschwindigkeitszunahme ist die Richtungsänderung. Das erklärt sich am besten mit Bildern der Geschwindigkeitspfeile. Siehe dazu die Links oben in #23 und #30.
@myself
Er sowieso, aber gemeint war natürlich sie, die Sonde.
Hallo Alderamin,
danke für Deine Antwort, den Wikiartikel hatte ich auch überflogen, aber er enthält keine Beschreibung des psysikalischen Effektes. Es gibt keine Energieübertragung wie bei Stößen, oder irre ich mich?
Denn Gravitation verhält sich genau anders herum, als Abstoßung. Komme ich einem Planeten näher, steigt die Anziehung, Kommt ein Ball einer Mauer näher steigt die Abstoßung. Diese Abstoßung fehlt aber im System Sonde – Planet. Darum frage ich nach dem Effekt dahinter.
Sorry fürs Nachhaken, aber ich muss noch einmal auf die Rechnung mit den 220km/h zurückkommen.
Der Ball kommt dem Zug aus Lokführer-Sicht mit 120 km/h entgegen, wird vom Zug beschleunigt und fliegt daher aus Zugsicht auch wieder mit 120 km/h weg.
Wenn der Werfer dann tatsächlich eine Geschwindigkeit von 220 km/h misst – und das muss er tun, weil er sonst dieselbe Geschwindigkeit misst wie der Lokführer – woher kommen die zusätzlichen 100 km/h? Woher kommt die Energie, um den Ball auf mehr als 120 km/h zu beschleunigen? Oder anders gefragt: Wo ist mein Denkfehler?
@Rotkaeppchen_online
Der Effekt ist die Änderung des Geschwindigkeitsvektors. Wie gesagt, wenn die Richtung der Sonde beibehalten würde, gäbe es keinerlei Geschwindigkeitänderung. Durch die Änderung der Richtung ändert sich der Geschwindigkeitsvektor. Im System des Planeten ändert er sich dem Betrage nach nicht, im externen, relativ zur Sonne, schon. Der Spektrum-Artikel in #30 ist da sehr aufschlussreich, er betrachtet die Hyperbelbahn vereinfacht als eine instantane Änderung der Richtung und erklärt mit Pfeildiagrammen, wie sich die Geschwindigkeit ändert.
Dazu gibt es sonst nicht viel zu sagen. Nur, dass die Energie, die die Sonde gewinnt, dem Planeten entzogen wird, aber davon merkt er wegen seiner großen Masse nicht viel. Und dass die Umlenkung von der Geschwindigkeit der Sonde, der Masse des Planeten und der Entfernung beim Vorbeiflug abhängen.
@tomtoo
M.E. ist kein Unterschied zwischen elastischem Stoß und Swing-by, falls man davon ausgeht, dass es keine Dissipation gibt (etwa durch Reibung in der oberen Atmosphäre) und auch keine Triebwerke während des Swing-by aktiviert werden.
1) Es gilt Energieerhaltung
2) Es gilt (Dreh-)Impulserhaltung
3) Die Massen von Planet und Sonde ändern sich nicht, d.h. es gibt kein Masseaustausch.
Aus diesen Gründen ergibt sich für beide Szenarien die gleiche Berechnung, d.h. Swing-by kann als elastischer Stoß betrachtet werden.
Insbesondere liegen Schwerpunkt des Planeten und Trajektorie der Sonde in einer Ebene; zumindest falls man sich nicht zu weit vom Planeten entfernt und es daher ein Zweikörperproblem bleibt.
@nur Consuela
Von der Bewegungsenergie des Zuges.
Sprich der Zug wird ein klein weiniger langsamer.
Mit dem swingby ist es in meinem laienhaften Verständnis ganz einfach: die Sonde „fällt“ etwas steiler in die Umlaufbahn des Planeten, zur Eigengeschwindigkeit „zieht“ noch zusätzlich die Schwerkraft in die gleiche Bewegungsrichtung und die Sonde wird genau deshalb beschleunigt. Zum Abbremsen muss die Sonde nur eine Flugbahn einnehmen, in der die Schwerkraft des Planeten entgegen der Bewegungsrichtung der Sonde „zieht“ und die Sonde bremst ab.
Soweit, sogut.
Aber auch auf die Gefahr hin, es tot zu reiten, das Zugbeispiel versteh ich einfach nicht.
Mir gehts da genauso wie „nur Consuela“:
Der Ball fliegt auf den Zug zu und prallt ab. In dem Augenblick, wo er auf den Zug aufprallt, würde er, wenn der Zug still stehen würde, mit annähernd gleicher Geschwindigkeit abprallen. Ball hat also im Wegfliegen immernoch rund 20km/h. Da der Zug aber nicht stillsteht, wird dem Ball die Geschwindigkeit des Zuges „mitgegeben“. Zug 100 km/h + Ball 20 km/h sind 120 km/h. Und das ist die Ballgeschwindigkeit, die der Beobachter messen sollte.
Es sind die „zusätzlichen“ 100 km/h, die ja irgendwo herkommen müssen, um am Ende den Ball mit 220 km/h zu messen, die mir große Schmerzen bereiten. Der Ball müsste dazu ja vom Zug DOPPELT so viel Geschwindigkeit mitbekommen, als der Zug tatsächlich fährt.
Wie soll das denn gehen?
@Knut:
Es wird keine Geschwindigkeit weitergegeben, sondern ein Impuls.
Der Zug hat natürlich einen viel größeren Impuls als der Ball. Meiner Meinung nach kann der auch viel schneller als 220km/h werden.
In diesem Gif sieht man das sehr schön, 😀 , wie der Impuls des langsamen Balls das kleine langsame Meerschweinchen sehr schnell macht…:
https://9gag.com/gag/aXEbG6d/hamster-exercise-ball-wtf
@Frantischek
Ich meine, bei deinem gif liegt das aber daran, dass sich sowohl das Meerschweinchen beim Auftreffen des Balls ein wenig „in“ den Ball hineinbewegt und gleichzeitig sich (aus Sicht des Fußbodens) der Fußboden „in“ den Ball bewegt. Also der Ball verformt sich gleichzeitig von oben und unten und beim Abprallen gleicht er beide Verformungen wieder aus, deshalb addieren sich die Beschleunigungen zu so eindrucksvollen Ergebnissen.
Für das Zugbeispiel scheint mir das aber nicht zu taugen, denn der Zug verformt sich ja nicht.
Bitte nicht mißverstehen, wenn hier so viele Leute die 220 km/h vertreten, neige ich dazu, denen zu glauben.
Aber ich verstehe diesen enormen Zuwachs von 100 km/h einfach nicht, das scheint mir zu viel zu sein.
Wenn man es nur mit dem Aufaddieren erklärt, könnte der Ball ja theoretisch bis auf unendliche Geschwindigkeiten kommen, wenn man ihn nur lange genug hin- und herprallen lässt. Und spätestens da kann doch irgendwas nicht hinhauen ?
@knut: Genau das kannst du, wenn du zwei Züge nimmst, die aufeinander zufahren und den Ball zwischen sich hin und her prallen. Aber nicht bis unendlich sondern nur bis Bad Aibling.
@Knut
Eigentlich ist es ganz einfach: schmeißt Du einen Ball mit der Geschwindigkeit v gegen die Wand und wird er elastisch reflektiert, dann prallt er mit v zurück, hat also vektoriell von -v auf +v beschleunigt, das sind 2v Geschwindigkeitaunterschied.
Aus Sicht des Zuges kommt der Ball mit -120 km/h entgegen und prallt also mit +120 km/h ab. Das System des Zuges bewegt sich aus Sicht der Schienen mit plus 100 km/h, also gelten in diesem System alle Geschwindigkeiten aus dem System des Zuges +100 km/h: anfliegender Ball -120 km/h + 100 km/h = 20 km/h. Zug: 0 km/h + 100 km/h = 100 km/h. Reflektierter Ball 120 km/h + 100 km/h = 220 km/h.
Wie gesagt, ich verstehe das so, dass der Ball mit gleicher Geschwindigkeit wegprallt, wie anprallt. (Reibungsverluste etc lassen wir mal aussen vor)
Und dabei ist es ja Jacke wie Hose, ob der Ball mit 20 km/h auf eine Wand prallt, die ihm mit 100 km/h entgegen kommt, oder ob der Ball mit 120 km/h auf eine stillstehende Wand prallt.
Die Geschwindigkeiten beider Protagonisten addieren sich.
Damit wars das aber schon. Um über 120 km/h zu kommen, muss von irgendwoher Energie in das System rein. Woher kommt die?
Vielleicht habe ich ja wirklich einen Denkfehler, aber ich kann ihn ums Verrecken nicht finden.
Für mich sieht es so aus, dass in Florians Beispiel die Geschwindigkeit vom Zug zweimal mit reingerechnet wird und ich versteh den Grund dafür einfach nicht.
Sorry, wenn das nervt, aber ich wills einfach verstehen, wie das geht.
Gibts da kein Beispiel, wo das mal einer tatsächlich gemessen hat, damit man sich mal ein Bild davon machen kann?
@Alderamin
Mein Text und deine Antwort haben sich überschnitten.
So wie du das erklärst, leuchtet mir das ein.
Der Punkt, auf des es ankommt, ist die Sicht der Schiene, im Beispiel die Sicht des Werfers, der sich gegenüber Zug und Ball nicht bewegt.
Ich hatte das übersehen und nur Zug und Ball berücksichtigt. Sorry, dass ich mich so blöd angestellt habe.
@Knut
Genau, das ist auch mein Verständnisproblem. Für mich sieht es so aus, als würde der Zug doppelt so viel Energie weitergeben als er „eigentlich“ sollte. Ich hätte, so wie Florian ursprünglich, auch einfach die beiden Geschwindigkeiten addiert.
Um das Beispiel zu vereinfachen: Wenn der Ball auf den Geleisen liegt (also ruht) – fliegt er dann mit 200 km/h weg, obwohl der Zug nur 100 km/h schnell ist?
Auch ich kam bis zum Hamster nicht ganz mit den 220 km/h zurecht.
Das Problem liegt hier wohl im gedanklichen Trennen von Modellrechnung ohne äußere Einflüsse und den persönlichen Erfahrungen aus dem realen Leben. Zusätzlich komplex machen es unterschiedliche Bezugssysteme und verschiedene Geschwindigkeiten, die anfangs auch noch entgegengesetzt gerichtet sind.
Lassen wir mal die zusätzlichen 20 km/h weg und sagen der Ball schwebt vor dem Zug, dann ist es leichter vorstellbar, dass sich der Ball nach dem Aufprall mit einer Geschwindigkeit > 100 km/h in Richtung Bahnhof bewegt. Wie schnell, klärt die Mathematik.
@nur Consuela
Genau richtig. Aus Sicht des Zuges kommt er dann mit -100 km/h entgegen und wird mit +100 km/h reflektiert. Von außen besehen alles +100 km/h: -100 + 100 = 0, 100 +100 = 200.
Die Energie kommt aus dem Unterschied der Massen von Zug und Ball. Der Zug gibt einen Teil seiner kinetischen Energie, die in der bewegten Masse steckt, an den Ball ab. Bei dem geringen Gewicht des Balls drückt sich diese Energie in hoher Geschwindigkeit aus.
So, Alderamin, und jetzt stellst du dir den Zug als Planeten vor, Massepunkt, durch den die gerade drauf zufliegende Sonde durchfliegen kannst, und du erkennst, daß für die Geschwindigkeitszunahme der Sonde im Bezugssystem Sonne eine Richtunsänderung nicht nötig ist.
In der Realität muß die Sonde natürlich am Planeten vorbei, wodurch man noch zusätzlich die Uberttagung von Bahndrehimpuls vom Planeten auf die Sonde kalkulieren muß.
Okay, danke – jetzt komme ich der Sache gedanklich näher. Einmal aber trotzdem noch:
Mal angenommen die Masse des ruhenden Balles und des Zugs sind ident – dann haben wir sozusagen eine Billiard-Situation, in der der Zug seinen gesamten Impuls auf den Ball überträgt und stehenbleibt, richtig? Der Ball aber rollt mit der ursprünglichen Geschwindegkeit des Zugs weiter, also 100 km/h.
Und genau da stehe ich offenbar auf der Leitung, weil mein Hirn eigentlich keinen grundsätzlichen Unterschied zwischen den beiden Situationen sieht.
@nur Consuela:
Genau richtig, wenn beide Massen gleich sind! (Und aus gleichem Material)
Sind sie hier aber nicht. Nehmen wir an, es wurden 200 Liter (?) Diesel verbrannt, um den Zug von vielen Tonnen auf 100 km/h zu beschleunigen. Diese Engerie ist dann als kinetische Energie im Zug gespeichert.
Nun reicht bereits ein ganz kleiner Bruchteil dieser Energie, um den Ball von ein paar Gramm auf > 200 km/h zu beschleunigen.
Und weil nur ein Bruchteil der Energie des Zuges auf den Ball übertragen wird, wird der Zug in dem Fall zwar auch langsamer, aber das lässt sich wohl kaum messen, geschweige denn mit bloßem Auge sehen.
Die o. g. Näherung, daß wir zum Bezugsystem „Zug“ wechseln und den Ball daran elastisch reflektieren lassen, funktioniert nur deswegen so einfach, weil der Zug vielviel mehr Masse hat als der Ball. Wenn beide gleich schwer sind, ist’s auch einfach: Impulserhaltung sagt, daß der Zug nach dem Stoß den Impuls des Balles übernommen hat und mit 20kmh rückwärts rollt, der Ball andersrum mit 100kmh wieder zurück fliegt (beide je aus eigener Sicht und in Bezug zum ruhenden Beobachter).
@pederm
Öh, doch, der Flyby entspricht in etwa der Situation, dass der Ball von seitlich die Lok trifft und dann von ihr nach vorne katapultiert wird. Auch bei frontalen Zusammenstoß mit dem Ball ändert dieser seine Richtung.
Wenn die Sonde den Planeten geradlinig in oder gegen sein Bahnrichtung durchfliegen könnte, gäbe es keinen Geschwindigkeitszuwachs. Den Zuwachs gibt’s wegen der seitlichen Komponente, die der Planet der Sonde mitgibt. Sie kreuzt hinter ihm seine Bahn und wird dann seitlich von ihm mitgezogen.
Wir müsste ich das eigentlich rechnen, wenn 2 massereiche Bälle aus unterschiedlichen Winkeln mit unterschiedlichen Geschwindigkeiten zeitgleich im gleichen Punkt auf den Zug treffen?
Hatte vor längerer Zeit schon mal im Internet geforscht, aber auf die schnelle nichts hilfreiches gefunden. Gibt es dafür eine analytische Lösung?
@JoJo,@all
Ich glaube ich habe das jetzt verstanden.
Ist ersten Moment war das nicht sofort zu durchdringen für mich.
Also Danke !
Ich versuchs mal mit meinen einfachen Worten zu beschreiben (wer lacht fliegt) 🙂 .
Also würde ich auf den Schienen stehen und den Ball direkt auf den Zug werfen mit 20km/h würde er auf den Zug (100km/h) prallen und kommt mir dann von mir aus betrachtet mit 220km/h zurück. 100 km/h hatt der Zug der Ball prallt vom Zug ab und entfernt sich vom Zugführer mit der Geschwindigkeit die der Zug hatt. Ergo der Ball kommt mir mit 220 km/h entgegen( nicht fangen ! ). Bei einem Swing bei würde das gleiche passieren (Reibung usw. vernachlässigt)nur das er halt nicht abprallt, sondern ne 180 Grad Kurve um den Planeten machen würde ?
Alles andere sind dann Vektoren usw.
Ist das richtig verstanden ?
@Marcel, Alderamin
Langsam dämmert’s mir, dass es tatsächlich um den Masseunterschied geht. Wenn der Zug (im Beispiel mit dem ruhenden Ball) nur ein bisschen massereicher ist als der Ball wird der Ball auf einen Wert irgendwo zwischen 100 und 200 km/h beschleunigt und der Zug entsprechend verlangsamt.
Und je größer der Massenunterschied zwischen Ball und Zug ist desto näher kommen wir den 200 km/h. Richtig so?
@tomtoo #72
Das war sprachlich immer noch nicht ganz richtig.
Der Ball entfernt sich vom Zugführer mit 120 km/h kommt also auf den Werfer mit 220 km/h zurück. So ist es glaube ich richtig.
@tomtoo
Die Empfehlung „nicht fangen !“ ist eigentlich unerheblich, dieweil ja gleich darauf noch ein weiteres Objekt mit ca. 100 km/h beim Werfer ankommt.
@Kyllyetti
https://l7.alamy.com/zooms/360c1ae1c7424e0ea6af284851194966/computer-games-moorhuhn-c974n2.jpg
😉
Super, an alle!
Wie schnell ein Alter Hase sich mit solchen einfachen Gedankenexprimenten auf das Glatteis führen lässt.
Der Gedanke mit dem ruhenden Ball beim Zusammenstoss war der einleuchtendste.
Deshalb ist die Physik die Königin unter den Naturwissenschaften.
@Frantischek:
Schönes „Anschauungsbeispiel“, an dem auch das Prinzip der Entropie gut studieren kann 😉
@nur Konsuela
Die Masse wird vernachlässigt weil sie im Verhältnis Zug-Ball nicht wirklich relevant ist.
Saturn,Jupiter vs. Sonde noch viel,viel mehr gegen null tendiert.
@tomtoo:
Kapier ich nicht. Kannst du das nochmal ausformulieren ?
@Steffmann
Bei meiner Rechtschreibung bekämst du Augenkrebs auch nur beim Versuch der Ausformulierung.
@Tomtoo:
Ach was, du bist bloß zu faul, gib es zu ;-). Aber gut, dann frage ich auch nicht, was Du mit Verhältnis Zug-Ball meintest
@Steffman
Du ich hab echt keinen Plan.
Ich versuche nur zu verstehen.
Erzähl über Entropie !
Tomtoo meint sicher, dass der Impuls p=m*v vom Zug, durch seine grosse Masse gegenüber dem Impuls vom Ball, sehr gross ist. Wird ein Impuls zwischen Zug und Ball ausgetauscht, so macht sich das in einer Geschwindigkeitsänderung auf Zug und Ball bemerkbar, da ja die Massen konstant bleiben. Ein Impulsaustausch hat wie man leicht überlegen kann, eine grosse Auswirkung auf die Geschwindigkeit vom Ball nach dem Impulsaustausch, während die Geschwindigkeit sänderung beim Zug zu vernachlässigen ist.
@Tomtoo
Entropie ist ein geiles Ding. Ich kann das regelmäßig in meiner Küche beobachten 😉 Und ich habe auch keinen Plan, ich frage nur
@Karl-Heinz:
Ist mir jetzt schon klar. Ich hatte anfangs Probleme mit der Formulierung von #tomtoo, klang etwas wirr. Hat sich jetzt ja aufgeklärt. Trotzdem danke für die Mühe.
@Steffmann
Ich weiß.
Wollte nur tomtoo’s Gedanken etwas ordnen.
@Steffmann
Danke Karl-Heinz !
Echt so Dumpfbacken wie ich müssen über soetwas nachdenken.
Aber es wird langsam klarer.
@Steffmann
Küche ? Entropie ? Faul ?
OK !
Oh misst sry.
Wie bilden sich Sonnen ,Planeten entgegen der Entropie ? Sollten wir nicht alle ein dünnes Gas sein ?
Kräfte die gegen die Entropie wirken ?
Gravitation,EM..die Kernkräfte ?
Ich hab keinen Plan ?
@tomtoo:
Dumpfbacken fragen hier auf Astrodicticum Simplex nicht, sondern motzen nur. Ergo, kannst Du nicht zu dieser Spezies gehören 😉
@Florian #38:
Auf der verlinkten Nasa-Seite ist es korrekt. Auch wenn der Satz, der mit „The ball …“ beginnt, falsch interpretiert werden kann, wenn man nicht merkt, in welchem Bezugssystem die jeweiligen Geschwindigkeiten gelten.
@tomtoo
Die bilden sich nicht entgegen der Entropie, sondern mit der Entropie. Ein Gas in einer Druckflasche, die man öffnet, verteilt sich, wegen des inneren Drucks, der nach außen wirkt. Die Entropie steigt, wenn sich das Gas möglichst weiträumig verteilen kann, weil es dann mehr mögliche Anordnungen der Teilchen gibt, als in einem kleineren Volumen.
Im Weltall bewirkt die Gravitation zuerst mal eine Kompression, dabei steigt die Teilchengeschwindigkeit, was zunächst eine Entstehung von Strukturen eher behindert (weswegen Dunkle Materie etwa keine Objekte bildet). Damit die Teilchen irgendein Objekt formen können, müssen sie unelastisch stoßen und ihre Bewegungsenergie loswerden (wir sprachen schon einmal darüber, dass Schwarze Löcher keine Staubsauger sind und wie schwer es wäre, Atommüll in die Sonne zu befördern). Das setzt Wärme frei, und die erhöht insgesamt die Entropie. Supermassive Schwarze Löcher, in die Material fällt, gehören zu den hellsten Objekten im Universum und die Planeten sind im Inneren noch immer heiß aus der Zeit ihrer Entstehung. Siehe auch hier.
Danke für die Frage, ich wusste zwar bisher, dass der Ausgangszustand des Universums mit gleich verteilter Materie eine niedrigere Entropie hatte, als die heutige Struktur des Weltalls, aber wieso genau wurde mir erst durch das Lesen des Links oben klar.
@Alderamin
Vielen Dank !
Von der Seite hab ich das ganze noch nie betrachtet.
So macht es dann ja auch Sinn.
@all
Enschuldigung für’s OT kam über die Küchenentropie irgentwie da rein.
@alderamin #69
Hast vollkommen recht! Man soll nicht während der Arbeit (nachmittags bis nachts) an Blogdiskussionen teilnehmen und schlaues Zeug schreiben wollen. Hoffentlich hab ich niemanden noch zusätzlich verwirrt.
Gedankenexperiment, (physikalisch unmöglich, es geht nur um die Denklogik)
Der Zug nähert sich mit Lichtgeschwindigkeit.
Was macht der Ball?
a) bleibt er an der Frontscheibe kleben
b) prallt er ab ?
@Robert
Ich nehme an, du gehst in deinem Gedankenexperiment von einem elastischen Stoß aus.
Wenn ja, so kann ich dir deine Frage beantworten.
@Robert
Gedankenexperiment – physikalisch unmöglich(!).
@Robert
Ach ja, das hätte ich fast vergessen.
Da der Zug eine Ruhemasse hat, kann dieser sich nur mit einer Geschwindigkeit bewegen, die unter der Lichtgeschwindigkeit ist. Dieser Sachverhalt ist für dieses Gedankenexperiment extrem wichtig.
@Robert: Die beobachteten Geschwindigkeiten lägen immer unter der Lichtgeschwindigkeit. Relativistische Effekte wären allerdings zu erwarten.
@Captain E.
Aus der Sicht des Zugführers ist der Impuls des Balls naher der Lichtgeschwindigkeit unter Umständen gigantisch.
Bin schon gespannt wenn man’s rechnet, was rauskommt.
Wer Züge oder Bälle auf relativistische Geschwindigkeiten beschleunigt, sollte vielleicht beachten, dass dabei einige störende Nebeneffekte auftreten, welche die Freude am erfolgreichen Experiment mindern könnten.
Karl-Heinz,
stimmt , das ist sogar ausschlaggebend. Also…
Nachtrag: Der Ball hat keine Masse.(das ist nur ein Gedankenexperiment!)
in etwa vergleichbar mit einem Photon.
Der Zug hat Masse und bewegt sich fast mit Lichtgeschwindigkeit.
@Robert
Misst, der Ball muss Masse haben, da ich sonst keinen Impuls zusammenbekomme.
Wir könnten auch ein Photon nehmen, aber dann ist das Ergebnis ganz anders.
Ach ja, das Photon ist immer mit Lichtgeschwindigkeit unterwegs, da es keine Ruhemasse hat.
@Kyllyeti
Du hast mit dem störenden Nebeneffekte Recht.
Die blenden wir aber beim Gedankenexperiment aus, wenn’s dir nix ausmacht.
Karl-Heinz,
…das Photon ist immer mit Lichtgeschwindigkeit unterwegs. (vom Zug aus betrachtet)
vom Photon aus gesehen bewegt sich der Zug fast mit Lichtgeschwindigkeit.
Also was macht das Photon, wenn es auf die Zugscheibe prallt? Und was sieht der Zugführer?
@Robert
Für das Photon vergeht keine Zeit, da es mit Lichtgeschwindigkeit unterwegs ist.
Falls der Zug (Oberfläche der Front des Zuges sollte ein Spiegel sein) das Licht reflektiert, so sieht der Lockführer, dass sich das Licht nach der Reflexion mit Lichtgeschwindigkeit entfernt. Welche Farbe des Lichtes (Frequenz) der Lockführer wahrnimmt, muss man aber ausrechnen.
Super,
zu dieser Lösung bin ich auch gekommen. Die Aufgabe stammt aus keinem Buch, die ist mir vorhin spontan eingefallen.
Ursprünglich wollte ich das Photon stillstehen lassen.
Physikalisch gesehen ist diese Lösung besser.
Die Aufgabe mit den 220 km/h habe ich einem Freund gepostet. Der kommt über die Denkschwelle mit 120 km/h nicht hinaus.
@Kyllyeti
…halb so wild, das wesentliche ist doch „elegible to advance to the first base.“.
@Kyllyeti, StefanL
Ich bin da skeptisch. Der Fänger ist ja schon verdampft bevor er vom Ball getroffen wurde. Ich mein jetzt rein rechtlich. Er wurde also nie getroffen. Und der Werfer hat nur seinen Job (sozusagen perfekt) gemacht.
Nicht gefangen , ist nicht gefangen. 😉
@Kyllyeti, StefanL
sry fänger=battter
@Kyllyeti
Ha, ha „einige störende Nebeneffekte“
Der Witz der ist gut.
Ein Baseball mit 90% der Lichtgeschwindigkeit hat eine Bewegungsenergie
von 312 Hiroshimabomben.
—————————————————————————————————
Hiroshimabombe (Little Boy) Sprengkraft von etwa 13 Kilotonnen TNT
1 kT (Kilotonne TNT) = 4,184 · 10^12 J
Little Boy hat demnach eine Energiefreisetzung von 5,4· 10^13 J
Gewicht des Baseballs 0,145 kg
Geschwindigkeit des Baseballs = 0,9 c
Lorentzfaktor ϒ = 1/ (1-0,9^2) ^0,5= 2,29
Kinetische Energie des Baseballs Ekin = (ϒ-1) *m*c^2 = 1,68 * 10^16 J entspricht
in etwa 312 Hiroshimabomben
@tomtoo
…müßtest Du dazu aber nicht erst nachweisen, dass der Großteil der relevanten Gamma-quanten nicht vom Baseball stammt? Bzw. reicht nicht die Ursächlichkeit „Baseball“ selbst für die zerstrahlten Luft-Moleküle/Atome?
Andernfalls dürfte es sonst schwierig sein überhaupt von so etwas wie „Treffer“ zu sprechen, da immer mit „erst Luftstoß“ argumentiert werden könnte, oder?
Was wir hier haben ist ja sogar, dass die Luftmoleküle nicht mal genug Zeit zum Ausweichen haben…
hmm – ist hier ein Anwalt unterwegs … 🙂
Noch eine kleine Anmerkung: Das erste Swing-By-Manöver war m.W. die Rückkehr der Apollo 13 durch ein ebensolches Manöver um den Mond herum im April 1970.
[…] der Trojaner). Dann wird Lucy wieder zurück zur Erde fliegen und sich dort mit einem Swing-By-Manöver neuen Schwung holen. Der bringt sie zurück zum Jupiter, aber diesmal zur “L5-Gruppe” […]
Es hat mal ein Astrophysiker, und Science-fiction Fan, … die Idee geäußert: Massen von Minisonden, durch Swing-By, am Jupiter auf „beinahe Lichtgeschwindigkeit“ ???? zu beschleunigen, und sie dann in den Interstellaren Raum auf die suche zu schicken,
Das schien mir sofort unplausibel!!! spukt mir trotzdem noch im Kopf 😉
Kann wer bitte, … mit circa machbaren Geschwindigkeit dienen^^ (den Rechnungen mit Bällen kann ich noch selbst folgen ;)) denke aber das Swing-By.. wg der Masse nicht beliebig steigerbar ist.
@# 30 bis #60
mein Senf^^ ..beide seiten haben recht weil´s nur theoretisch:
wenn man den Gummi Impuls des Balls rechnet könnte 220 rauskommen, bei festen Körper dagegen würde der -20 km/h Impuls auf den Lok übergehen und vom Lok +100 km/h (ein Eimer beton würde gerade noch mitgeschleppt ;))
[…] Entfernung wächst. Wir müssen ihn einholen und das wird schwierig. Eine Möglichkeit wäre eine Swing-By-Mission bei der man sich bei Planeten Schwung holt. Je nach Missionsdauer zwischen 30 und 5 Jahren müssten […]
H-Anker,, die die Grundidee als Steinbruch benutzt.
Es sind maximal 0 von 14 Trophäen erspielbar.
Die Server der HK-Version sind noch online.