Hinweis: Dieser Artikel ist ein Beitrag zum ScienceBlogs Blog-Schreibwettbewerb 2016. Hinweise zum Ablauf des Bewerbs und wie ihr dabei Abstimmen könnt findet ihr hier.

Das sagt der Autor des Artikels, Pascal Meger über sich:
Ich bin Schüler der 12. Klasse des Vincent-Lübeck-Gymnasiums in Stade. Ich habe noch nie zuvor einen Blog geschrieben, aber wollte es einfach einmal ausprobieren.
——————————————
Radialgeschwindigkeitsmethode
In meinem Blog möchte ich Ihnen gerne die interessante Radialgeschwindigkeitsmethode näherbringen, die sich mit der Entdeckung von Exoplaneten befasst.
Exoplaneten, oder auch extrasolare Planeten genannt, sind Planeten, die sich außerhalb unseres Sonnensystems befinden und so nicht um unsere Sonne, sondern um andere Sterne, kreisen.
Um solche Planeten zu finden benutzt man verschiedene Methoden.
Beispielsweise die Transitmethode, die direkte Beobachtung, die Gravitationslinsenmethode und, wie in der Überschrift gegeben, die Radialgeschwindigkeitsmethode.
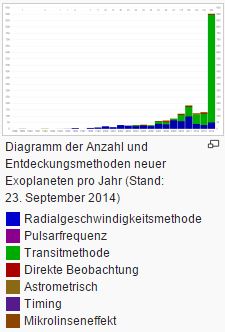
Auch Gemeinfrei von der Autorin Aldaron
So bewiesen Schweizer Forscher erstmals vor ungefähr 21 Jahren, dass es einen Planeten außerhalb unseres Sonnensystems gäbe.
Dieser Exoplanet erhielt den Namen „51 Pegasi b“. Dieser war schwerer als der Jupiter und war ein Gasplanet.
Mittlerweile (Stand 2016) gibt es durch diese Methoden 3406 entdeckte Exoplaneten.
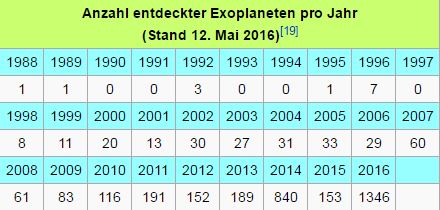
Für die Radialgeschwindigkeitsmethode ist der Dopplereffekt und die Spektroskopie von wichtiger Bedeutung.
Es gibt den akustischen und den optischen Dopplereffekt. Beim akustischen Dopplereffekt werden Schallwellen, die sich mit der Schallquelle bewegen, gestaucht und die, die sich von der Schallquelle entfernen, gestreckt.
Diesen Effekt kann man nun so ähnlich beim optischen Dopplereffekt anwenden.
Ein Planet, der sich um einen Stern dreht, zieht seinen Stern auch an, da einen Kraft vom Planeten auf den Stern wirkt, so aber auch von dem Stern auf den Planeten.
Dadurch rotiert der dazugehörige Stern auf einer Ellipsenbahn. Die elektromagnetischen Wellen des Lichtes werden in Richtung, in der sich der Stern bewegt, gestaucht und die Wellen, die sich gegensätzlich der Richtung bewegen, werden gestreckt.
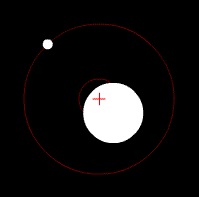
Dieses Werk wurde von seinem Urheber Zhatt als gemeinfrei veröffentlicht. Dies gilt weltweit.
Diese Wellen, die von einem Stern ausgehen, kann man nun mit Hilfe eines Spektroskopes auffangen.

Die elektromagnetischen Wellen treffen auf das Gitter des Spektroskopes, wodurch an einem Schirm ,oder auf einem elektrischen Gerät, einzelne Farbbänder projiziert werden.

Wenn sich nun ein Exoplanet in Richtung der Erde bewegt, dann bewegt sich auch sein Stern ein Stück in Richtung der Erde, wodurch die Wellen gestaucht werden. Dadurch ist die Wellenlänge kleiner, das zur Folge hat, dass die mit dem Spektroskop aufgefangenen Farbbänder blauverschoben sind. Entfernt sich nun ein Exoplanet wieder von der Erde, werden die Wellen gestreckt, so dass die Wellenlänge größer wird und die Farbbänder rotverschoben sind.
Generell analysiert man bei der Radialgeschwindigkeitsmethode nur die Farbbänder eines Sternes durch ein Spektroskop.
Wenn sich nun regelmäßig die Farbbänder in einem Spektroskop in den roten und blauen Bereich verschieben, bedeutet das, dass sich der Stern der Erde nähert und entfernt.
Und das passiert ja, wie bereits beschrieben, dadurch, dass sich ein Exoplanet um den Stern dreht und eine Anziehungskraft auf den Stern wirken lässt. So gilt das, wie bereits von Isaac Newton formulierte, Wechselwirkungsprinzip, in dem gilt, dass wenn ein Körper B eine Kraft auf einen anderen Körper A ausübt, gleichfalls Körper A eine gleichgroße entgegen gerichtete Kraft auf Körper B ausübt.
Durch die regelmäßige Veränderung der Farbbänder, lässt sich erschließen, dass sich ein oder mehrere Planeten um den Stern bewegen. Dafür muss der Planet noch nicht einmal optisch erfasst worden sein.
Wenn man nun die Masse des Sternes ermitteln kann, kann man auch die die Masse des Exoplaneten berechnen, denn um so schwerer der Exoplanet, desto größer die Ellipsenbahn des Sternes, da eine größere Kraft auf den Stern wirkt. Des Weiteren kann man erkennen, welche Umlaufzeit der Exoplanet um seinen Stern hat. Man muss nur beobachten wie lange es dauert, dass eine Rotverschiebung einsetzt, vorübergeht und erneut einsetzt. Die gemessene Zeit beträgt ungefähr die Umlaufzeit des Planeten.
Diese Methode hat dennoch den Nachteil, dass man mit ihrer Hilfe nur größere Planeten entdecken kann, da sie eine bestimmte Massen besitzen, um den Stern in eine Rotationsbahn zu bringen. Denn ein kleiner Planet kann bei einem großen Stern kaum eine Anziehungskraft aufbringen, die groß genug ist, um zu rotieren.
Dennoch sind viele Exoplaneten sehr groß, wodurch schon durch diese Methode knapp 604 Planeten entdeckt wurden (Stand: 24. Juli 2015).
Des Weiteren sind die Formeln zum Berechnen der Massen und Größen der Exoplaneten so kompliziert, dass ich sie nicht weiter erläutern werden.
Am Ende stelle ich mir die Frage, möglicherweise Sie auch, warum man sich so einen Aufwand macht, solche Planeten zu entdecken. Die Geräte dafür sind ja ziemlich teuer und zum Beobachten benötigt man sehr viel Zeit.
Ich denke, dass einer der Hauptgründe unsere Neugierde ist. Die Frage ist ja immer noch offen, ob wir alleine in diesem Universum sind, oder ob es noch andere Lebewesen gibt.
Manche der entdeckten Planeten ähneln der Erde, aber manche sind auch nur Gasriesen.
Des Weiteren stelle ich die Vermutung auf, dass die Exoplaneten, gerade erdähnliche Planeten, irgendwann im Laufe der Menschheit eine wichtige Rolle spielen könnte.
Stelle man sich einmal das Szenario vor, dass die Rohstoffe ausgehen.
Im Nachhinein gar nicht so unwahrscheinlich. Rohstoffe, wie Wasser oder fossile Brennstoffe werden immer knapper. Es könnte ja passieren, dass wir irgendwann Exoplaneten nutzen könnten, um solche Stoffe zu gewinnen und den Fortbestand der Menschheit zu sichern.
Dazu besteht auch die Möglichkeit, dass irgendwann die Menschen ihren Lebensraum selber komplett zerstört haben, indem sie weiterhin umweltschädliche Gase in die Atmosphäre strömen lassen.
Diese Szenarien müssen ja nicht eintreten, aber es könnte passieren. In diesen Fällen wäre ein erdähnlicher Exoplanet vielleicht hilfreich.
Es ist schon bewundernswert, wie die Forschung Dinge „sichtbar“ macht, die man nicht sehen kann. (bildhaft gesprochen)
Sieht man die Verschiebung der Farbbänder auch an z.B. den Jupitermonden?
Hmmm, wenn die beiden sich um den gemeinsamen Schwerpunkt bewegen und der Planet relativ dazu ’nach vorne‘ kommt, müßte sich da nicht der Stern in den relativen Hintergrund zurückziehen?
Wo ist mein Denkfehler?
Exoplanet bewegt sich in der halben Drehung in Richtung der Erde und gleichzeitig bewegt sich auch der auch sein Stern in der halben Drehung in Richtung der Erde.
Das kann nicht funktionieren, da der Gesamtimpuls von Exoplanet plus seinem Stern zeitlich nicht konstant wäre.
Beide bewegen sich auf uns zu und dann wieder von uns weg. Das wäre ein lustiges Gespann 😉
Mein erster Gedanke war ja ‚Echternach‚, Karl-Heinz – aber (auch) die machen das nicht ;‑)
Coole Sache, das mit der Echternacher Springprozession 🙂
https://www.youtube.com/watch?v=k-n_XhVJkY0
@Pascal
Die ersten entdeckten Exoplaneten wurden sogar schon 1992 um den Pulsar PSR 1257+12 entdeckt, auch mit einer Radialgeschwindigkeitsmethode (Doppler-Effekt), allerdings auf die Pulsrate des Pulsars, nicht auf die Spektrallinien.
Korrekter wäre: die Spektrallinien (die übrigens dunkel sind), sind gegenüber den Spektralfarben verschoben. Die Position der Linien verändert sich dabei nur um einen winzigen Betrag. Das Spektrum eines für solche Messungen verwendeten Spektrographen sieht dann auch ganz anders aus als das oben im Bild. Die Farben alleine geben wenig Orientierung, die Linien sind hingegen sehr scharf und leichter zu messen (z.B. indem man sie mit einem auf der Erde erzeugten Referenzspektrum vergleicht).
Na ja, zum Einen sind die Exoplaneten so fürchterlich weit weg, dass die Menschheit sie möglicherweise niemals erreichen wird (und wenn, dann nur ein paar Menschen, die die Erde für immer verlassen werden). Zum Anderen gibt es genug Rohstoffe (außer den fossilen) im Sonnensystem, dazu braucht es nur die viel näheren Asteroiden. Und Wasser ist nicht wirklich knapp auf der Erde, sauberes Trinkwasser schon eher, aber nicht überall auf der Erde. Dafür braucht man nicht einmal in den Weltraum. Auf Curacao wird Bier gebraut – aus entsalztem Meerwasser!
Die Erforschung der Exoplaneten dient vor allem dazu, dass wir etwas über die Erde lernen: wie sie entstanden ist, wie typisch sie ist, wie typisch unser Sonnensystem insgesamt ist und was es sonst noch so gibt (z.B. Supererden). Das lernt man durch Vergleich mit den Planeten anderer Sterne.
ein Raumschiff´, das auf nur 3% der Lichtgeschwindigkeit beschleunigt und vor dem Ziel wieder abgebremst wird
, benötigt hierfür ca. das Tausendfache des jährlichen Energieverbrauchs der Erde. Wie soll die Erdbevölkerung dies so nebenbei aufbringen, v.a. wenn die Resourcen zu Ende gehen? Und wie soll diese Energiemenge in einem verhältnis kleinen Raumschiff untergebracht werden? Und diese Tatsache gilt auch für alle in Zukunft noch zu erfindenden Antriebe.
@gerhard beer:
Ekin = 1,00045 (Lorentzfaktor) * 0,5*m*v² *2 (fürs Abbremsen)
v=9*10^6 m/s
–> E/m = 8,104*10^13 J/kg
jährlicher fossiler Energieverbrauch der Menschheit: 104000 TWh (Stand 2012)
1 kWh entspricht 3,6*10^6 J.
1 TWh entspricht 3,6*10^15 J.
Welt entspricht 3,7*10^20 J (pro Jahr).
Andere Quellen geben insgesamt 5,2*10^20 J an.
Ihre Aussage wäre also nur dann richtig, wenn ihr „kleines“ Raumschiff 6 Millionen Tonnen wöge (5/8 * 10^7*10^3 („Tausendfache) kg). Das interstellare Reisen ist eben doch deutlich einfacher.
@Wizzy
Bist Du sicher das deine Formel Ekin stimmt.
Ich habe sie ein bisschen anders in Erinnerung.
@Karl-Heinz
Berechtigte Frage, bei genauerem Recherchieren hast Du mit Deiner kritischen Nachfrage wahrscheinlich recht (obwohl sich das so in meinen Grundstudiumsaufschrieben findet, der Prof war aber nicht vom Fach). Der Lorentzfaktor spielt aber bei 3%c nur eine geringe Rolle, man kann näherungswesie klassisch rechnen.
Ja, ich lag falsch. Allerdings macht das im vorgestellten Fall nur einen sehr geringen Unterschied aus. Korrekt wäre (Gamma-1)*m*c². Für Gamma –> sehr groß geht der Fehler dann gegen Faktor 2.
@Wizzy
………….
Stimmt
…………
Wird der Ausdruck Ekin = (Gamma-1)*m*c² in eine Taylor-Reihe entwickelt
Ekin = 0,5*m*v^2 + (3*m*v^4) / (8 * c^2)
, so kann man für kleine Geschwindigkeiten Glieder höherer Ordnung vernachlässigen.
Übrig bleibt dann der Term Ekin = 0,5*m*v^2.
Der optische Doppler-Effekt kann mit dem akustischen nur bedingt verglichen werden und entspricht ihm lediglich hinsichtlich des sekundären Doppler-Effekts. Aufgrund unterschiedlicher Radialgeschwindigkeiten eines Sterns werden die von ihm ausgehenden Lichtwellen nämlich keineswegs gestaucht bzw. gedehnt. Dieser von der Akustik herrührende Analogieschluß ist deshalb nicht zulässig, weil es beim Licht im Gegensatz zum Schall kein ausbreitungsgeschwindigkeitsbestimmendes Medium gibt, gegen das sich die Quelle unter damit einhergehender Veränderung der Wellenlänge bewegen könnte, wie uns das beim Schall als primärer oder eigentlicher Doppler-Effekt geläufig ist, den es beim Licht bekanntlich nicht gibt. Die zu beobachtenden Frequenzänderungen können daher nur durch unterschiedliche Relativgeschwindigkeiten zustandekommen!
Im übrigen darf die fehlerhafte Formel der Lorentz-Transformation überhaupt nicht verwendet werden, weil sie entgegen Einsteins unbewiesener Behauptung nicht einmal die unumgängliche Transitivitätsbedingung erfüllt, was bereits Max von Laue und Arnold Sommerfeld als conditio sine qua non forderten.
@Dipl.-Ing. Norbert Derksen
Das mit der Transitivitätsbedingung war mir bis jetzt unbekannt. Ich hoffe sie haben nichts gegen den unten angeführten Link.
https://www.relativ-kritisch.net/blog/kritiker/hypothesen-die-niemand-braucht-2-norbert-derksen
Den hab ich jetzt nicht verstanden …
vs.
Kannste das bitte nochmal näher erläutern?
@Bullet
Vergiss Norbert Derksen.
Seine Ansichten sind jenseits von Gut und Böse.
Auch seine Ansichten gegenüber Frauen sind nicht ohne.