Hinweis: Dieser Artikel ist ein Beitrag zum ScienceBlogs Blog-Schreibwettbewerb 2016. Hinweise zum Ablauf des Bewerbs und wie ihr dabei Abstimmen könnt findet ihr hier.

Das sagt der Autor des Artikels, „Herr Fessa“ über sich:
Ich bin Lehrer und unterrichte an der HTL Rennweg in Wien. Hin und wieder schreibe ich auf meinem eigenen Blog https://herrfessa.wordpress.com
——————————————
Komplexe Zahlen – eine geometrische Einleitung
Einleitung
Generell sind Zahlen etwas sehr Abstraktes. Es gibt z.B. nichts Konkretes worauf man zeigen und sagen könnte, das ist die Zahl drei. Es sind immer entweder drei Menschen, drei Kühe, drei Autos … Entsprechend gibt es für die Zahl drei die verschiedensten konkreten Darstellungen, z.B. 3 oder III.
Ausgehend von unseren Vorstellungen über reelle Zahlen, werden wir im Folgenden zunächst eine geometrische Darstellung der reellen Zahlen betrachten und die bekannten Rechenoperationen geometrisch konstruieren. Diese Darstellung und Konstruktionen können wir dann »leicht« zur Darstellung einer neuen Menge von Zahlen erweitern – den komplexen Zahlen.
Pfeile entlang einer Geraden
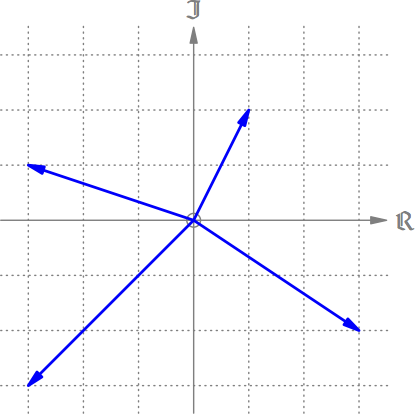
Nachdem man auf einer Geraden einen Ursprung 0 (werden wir immer als kleinen Kreis einzeichnen) und eine Einheit 1 festgelegt hat, kann man reelle Zahlen von 0 weg als Pfeile auf dieser Zahlengeraden (oder reellen Achse) einzeichnen (s. Abb. 1).
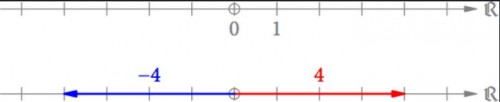
Abb. 1: Reelle Zahlen als Pfeile auf der reellen Achse. Die Pfeile der positiven Zahlen zeigen üblicherweise nach rechts.
Die Pfeile der negativen Zahlen zeigen dabei in die entgegengesetzte Richtung der entsprechenden Pfeile für die positiven Zahlen. Die Negation einer Zahl bedeutet also die Richtung umzudrehen.
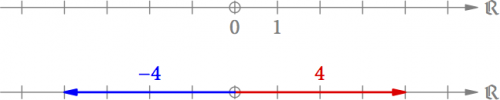
In der Zeichenebene kann man die Negation aber auch durch eine Drehung um 180° erreichen (s. Abb. 2). Die Winkel werden immer von der positiven reellen Achse aus gemessen, und irgendwann hat man sich geeinigt, dass eine Drehung gegen den Uhrzeigersinn ein vordrehen (eine positive Drehung) ist. Aus 4 wir durch so ein Vordrehen also -4 und durch ein weiteres Vordrehen -(-4) = 4, wie man es sich erwarten würde. Eine weitere Möglichkeit von -4 wieder zu 4 zu kommen, ist den Pfeil um 180° zurückzudrehen (im Uhrzeigersinn).
Abb. 2: Die Negation einer Zahl kann in der Zeichenebene auch durch ein Vordrehen um 180° erreicht werden.
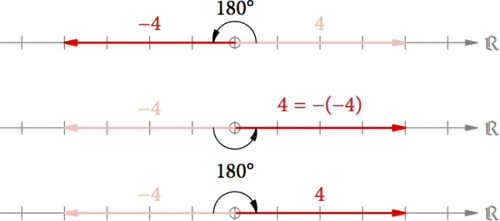
Können wir mit diesen Pfeilen auch rechnen, wie wir es mit den reellen Zahlen gewohnt sind? Ja, z.B. die Addition 2 + 3 = 3 + 2 = 5 (s. Abb. 3). Wir verschieben entweder den Pfeil für 3 parallel an das Ende des Pfeils für 2 oder umgekehrt. Die Summe ist dann der Pfeil vom Ursprung hin zur Spitze des verschobenen Pfeils. In beiden Fällen erhalten wir hier den Pfeil für 5. Bei unserer geometrischen Addition ist die Reihenfolge der Zahlen also genauso vertauschbar wie bei der rechnerischen.
Abb. 3: Die Addition 2 + 3 = 3 + 2 = 5 konstruiert durch Parallelverschiebung der Pfeile.
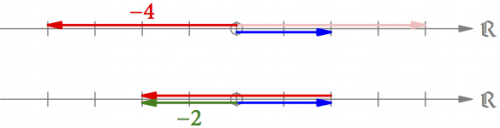
Da die Subtraktion nur eine versteckte Addition ist, können wir auf diese Art auch subtrahieren. Z.B. 2 – 4 = 2 + (-4) = -2 (s. Abb. 4). Zunächst negieren wir den Pfeil für 4 und addieren ihn dann wie gehabt zu 2 dazu.
Abb. 4: Die Subtraktion 2 – 4 ist dasselbe wie die Addition 2 + (-4) = -2.
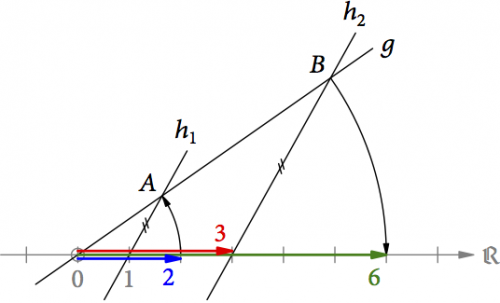
Die Multiplikation basiert auf einer Konstruktion von René Descartes. Fangen wir zunächst mit zwei positiven Zahlen an und konstruieren das Produkt 2 ⋅ 3 = 6 (s. Abb. 5). Wir zeichnen eine geneigte Gerade g durch den Ursprung 0. Dann drehen wir den Pfeil für die Zahl 2 um den Ursprung auf diese Gerade und erhalten den Punkt A. Durch diesen Punkt und die Einheit 1 auf der reellen Achse zeichnen wir die Gerade h1. Diese verschieben wir jetzt parallel ans Ende des Pfeils für die Zahl 3 (Gerade h2) und erhalten den Schnittpunkt B mit der Geraden g. Abschließend drehen wir Punkt Bzurück auf die reelle Achse und erhalten so den Pfeil für das Ergebnis 6.
Abb. 5: Die Multiplikation 2 ⋅ 3 = 6 nach René Descartes.
Die Konstruktion funktioniert, weil die Dreiecke 01A und 03B ähnlich sind. Nach dem Strahlensatz gilt daher 0B : 0A = 3 : 1, und weil 0A = 2 ist, ist 0B = 2 ⋅ 3 = 6. Hätten wir 3 ⋅ 2 konstruiert, wären nur die Steigungen der Geraden h1 und h2 anders gewesen (0B : 0A = 2 : 1 und 0A = 3). Auch in dieser Konstruktion ist wie in der Rechnung die Reihenfolge der Zahlen egal.
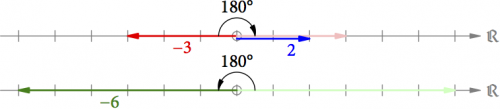
Was, wenn man eine positive mit einer negativen Zahl multiplizieren möchte, z.B. 2 ⋅ (−3) = −6? Aus der Algebra wissen wir: 2 ⋅ (−3) = −(2 ⋅ 3). Aha! Zuerst können wir aus dem Pfeil für −3 durch Drehung um 180° zurück den Pfeil für 3 machen (s. Abb. 6). Anschließend multiplizieren wir die beiden Pfeile wie oben beschrieben und erhalten den Pfeil für 6. Dieser Pfeil muss dann wieder um 180° vorgedreht werden, damit wir das Endergebnis −6 bekommen.
Abb. 6: Konstruktion der Multiplikation 2 ⋅ (-3) = -6.
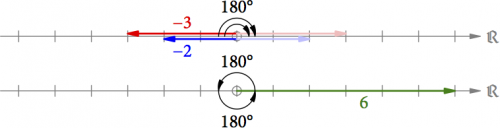
Wie sieht es zum Schluss mit der Multiplikation zweier negativer Zahlen wie (−2) ⋅ (−3) = 6 aus? Rein algebraisch gilt: (−2) ⋅ (−3) = −(−(2 ⋅ 3)). Zuerst drehen wir beide Pfeile um jeweils 180° zurück (s. Abb. 7) und multiplizieren sie wie gehabt. Weil wir aber zwei Pfeile um 180° gedreht haben, müssen wir das Ergebnis um 180° für den ersten Pfeil vordrehen plus noch einmal 180° für den zweiten Pfeil, wodurch wir wieder ein positives Endergebnis erhalten.
Abb. 7: Konstruktion der Multiplikation (-2) ⋅ (-3) = 6.
Dieses Hin- und Herdrehen bei der Multiplikation negativer Zahlen mag verwirrend sein, wird sich aber unten als Spezialfall einer allgemeineren Konstruktion erweisen.
Die Division ist die Umkehrung der Multiplikation; wir müssen den Konstruktionsgang also einfach genau von hinten nach vorne durchführen. Die Division 6 : 3 = 2 ist damit schon in Abb. 5 gezeigt.
Dass mit den obigen Konstruktionen auch die Assoziativitätsgesetze a + (b + c) = (a + b) + c und a ⋅ (b ⋅ c) = (a ⋅ b) ⋅ c gelten, kann man leicht nachprüfen. Selbiges gilt auch für das Distributivgesetz a ⋅ (b + c) = a ⋅ b + a ⋅ c, das Addition und Multiplikation verknüpft.
Da sich algebraisch alle Rechnungen mit reellen Zahlen auf diese Operationen zurückführen lassen, können wir folgern:
Alles, was man mit reellen Zahlen berechnet, könnte man genauso gut durch Konstruktionen mit Pfeilen entlang der reellen Achse erhalten.
Pfeile in einer Ebene
Wenn wir uns diese Konstruktionen aber genauer ansehen, stellt sich die Frage, warum wir uns nur auf Pfeile entlang der Zahlengeraden beschränken sollen. Das ganze können wir doch auch für beliebige Pfeile machen, die von der Geraden nach oben oder unten weg zeigen. (De facto haben wir das bei der Negation als Drehung um 180° ohnehin schon gemacht.)
Dazu fügen wir zu unserer reellen Achse eine weitere, senkrechte Achse hinzu. Aus rein historischen Gründen nennt man diese Achse die imaginäre Achse (s. Abb. 8). Im Prinzip sind reelle bzw. imaginäre Achse einfach die x– bzw. y-Achse der Ebene, man nennt sie hier nur anders. Der Ursprung 0 ist dort, wo diese beiden Achsen sich treffen. Außerdem werden die ganzzahligen Vielfachen der Einheit 1 jetzt auch nach oben und unten aufgetragen (punktiert in Abb. 8).
Abb. 8: Pfeile in der Ebene. Können wir auch damit »rechnen«?
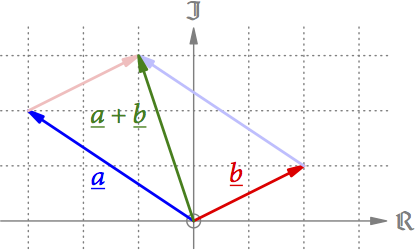
Die Addition der Pfeile a und b erfolgt wieder durch parallel verschieben des einen Pfeils an die Spitze des anderen (s. Abb. 9). (Um die Namen dieser Pfeile von gewöhnlichen reellen Variablen zu unterscheiden, werden sie oft unterstrichen.) Das ist eine völlig natürliche Erweiterung dessen, was wir entlang der Geraden gemacht haben, und die Reihenfolge der Pfeile spielt wieder keine Rolle.
Abb. 9: Addition von Pfeilen in der Ebene.
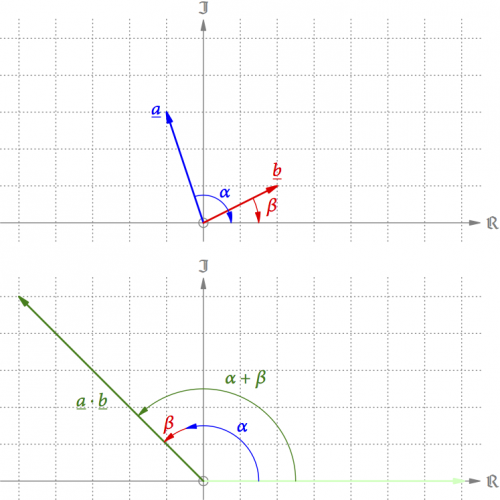
Für die Multiplikation erinnern wir uns an die Multiplikation mit negativen Zahlen zurück (s. Abb. 10). Wie dort drehen wir zuerst die beiden Pfeile um ihre jeweiligen Winkel zurück auf die positive reelle Achse. Dort multiplizieren wir sie nach der Methode von Descartes. Schließlich müssen wir dieses Zwischenergebnis zunächst um den Winkel der ersten Pfeils und dann noch um den Winkel des zweiten Pfeils nach vor drehen. Effektiv multiplizieren wir also die Längen der beiden Pfeile und addieren ihre Winkel. Geometrisch handelt es sich dabei um Drehstreckungen.
Abb. 10: Multiplikation von Pfeilen in der Ebene.
Auch diese Konstruktion ist eine natürliche Erweiterung von dem, was wir mit Pfeilen entlang der reellen Achse gemacht haben.
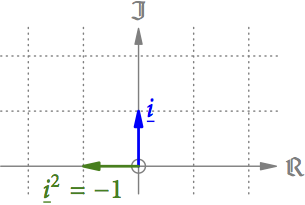
Eine interessante Folge dieser Multiplikation ergibt sich für den Pfeil i, der die Länge 1 hat und senkrecht auf die reelle Achse steht (s. Abb. 11). Multipliziert man ihn mit sich selbst (also quadriert man ihn), bleibt die Länge 1, aber der Winkel verdoppelt sich von 90° auf 180°. Man erhält also einen Pfeil, der der Zahl -1 entspricht.
Abb. 11: Quadriert man den Pfeil i (multipliziert ihn mit sich selbst), dann erhält man den Pfeil für die Zahl -1.
Zusammenfassung
Zunächst haben wir gesehen, dass man reelle Zahlen geometrisch als Pfeile entlang einer Geraden darstellen kann. Bestimmte Konstruktionen mit diesen Pfeilen führen zu Ergebnissen, die mit der bekannten Addition und Multiplikation von reellen Zahlen übereinstimmen. Alle diese Konstruktionen lassen sich auch auf Pfeile in der Ebene sinnvoll anwenden, d.h. man kann die Rechenregeln für reelle Zahlen auf Objekte erweitern, die über die reellen Zahlen hinausgehen.
Diese Pfeile in der Ebene können daher als geometrische Darstellung einer Zahlenmenge interpretiert werden, die echt größer ist als die Menge der reellen Zahlen. Man nennt diese Menge aus rein historischen Gründen die komplexen Zahlen. Für tatsächliche Berechnungen muss man sich für diese geometrische dann wieder die eine oder andere algebraische Darstellung plus Rechenregeln der komplexen Zahlen überlegen.
Ausblick
OK, wenn wir von der Geraden in die Ebene gehen, erhalten wir mit diesen Konstruktionen neue Zahlen. Was passiert, wenn wir jetzt noch die 3. Dimension dazu nehmen (oder die 4., 5., …)? Für die Addition/Subtraktion funktioniert die Sache genauso weiter, wie man sich das vorstellt (in mehr als 3 Dimensionen schon etwas schwierig).
Bei der Multiplikation hapert es aber. Unsere Konstruktion beruht darauf, dass Negation und Drehung um 180° dasselbe sind. In welcher Ebene sollen wir aber einen Pfeil im Raum um 180° drehen, um minus diesen Pfeil zu bekommen? Da gibt es unendlich viele Ebenen zur Auswahl.
Interessanterweise findet man bei Pfeilen in 4 Dimensionen fast so etwas wie eine Multiplikation. Nur auf die Vertauschbarkeit der Pfeile muss man verzichten. Diese Menge bilden daher keine »echten« Zahlen, und man nennt sie die Quaternionen.
In 8 Dimensionen gibt es nochmal Pfeile, die man multiplizieren kann, wenn man auch noch auf die Assoziativität verzichtet. Man nennt diese Menge die Oktaven (oder auch Oktonionen).
Darüber hinaus gibt es dann nichts mehr, was sich noch wie eine Zahl multiplizieren ließe. In diesem Sinne sind die komplexen Zahlen tatsächlich die größtmögliche Zahlenmenge.
ich war immer gut in mathe,
aber ich denke manch eine schüler hätte das besser verstanden, wenn er so eine tolle erklärung vor sich gehabt hätte.
sollte sofort als kopie an alle schulministerien gehen
grüssle
Faszinierend – ein Artikel über Komplexe Zahlen ohne den Begriff „Wurzel“ oder die Notationen wie a + i b bzw. der Exponentialdarstellung mit e und i.
@Mars63: Vielen Dank!
@Captain E.: Die vielen verschiedenen algebraischen Darstellungen komplexer Zahlen sind ja auch eine unerschöpfliche Quelle für Verwirrung bei Schülern.
a + i b = (a, b) = r∠phi = r e^phi
Der wirkliche Vorteil von a + i b ist, dass man beim Multiplizieren so tun kann, als würde man Binome ausmultiplizieren und sich nur i^2 = -1 merken muss.
r e^(i phi) natürlich!
@herrfessa
Wie wahr, wie wahr!
Habe den größten Teil bereits durchgearbeitet und selbst gezeichnet, werde das daheim mit Lineal und Zirkel nochmals tun. Wird meinen Mann sicher auch interessieren.
Ich gehöre zu denen, die sehr schlecht in Mathe waren, eigentlich eher in Rechnen, trotzdem war ich immer auch fasziniert davon. Besonders die imaginären Zahlen haben es mir damals angetan.
Sehr, sehr guter Beitrag! Gehört sicher zu meinen Favoriten.
@herrfessa:
Das ist die bevorzugte Notation bei Elektrotechnikern. Die nutzen die komplexen Zahlen in genau dieser Notation gerne, um Blindströme, -spannungen und -widerstände zu behandeln, die sich durch die Verwendung von Spulen und Kondensatoren ergeben.
Vielen Dank für den tollen Artikel. Das ist bisher die anschaulichste Erklärung der komplexen Zahlen die ich kenne – Klasse.
Ich beneide Ihre Schüler… Meine Mathelehrerin hat mir damals durchgehen lassen, dass ich keine Hausaufgaben mache – im Gegenzug dafür, dass ich keine unangenehmen Fragen im Unterricht stelle.
Bisher auf jeden Fall einer meiner Favoriten!
Danke für den wirklich anschaulichen Beitrag. Leider sitze ich noch im Büro, aber heut‘ Abend werde ich auch zu Geodreieck und Zirkel greifen, ich bin eher der haptische Typ 😉
@herrfessa
Das ist ja die gute alte Versor Form 😉
Ein Versor ist ein Drehzeiger in einer Schreibweise, die in der elektrotechnischen Literatur im Bereich der komplexen Wechselstromrechnung zu finden ist.
@Ursula, @Till, @Mechaniac: Danke!
@Captain E., @Karl-Heinz: Im ET-Unterricht ist die Versorform auch meine bevorzugte Wahl, weil etwas kompakter als die Exponentialform.
Bzgl. komplexe Zahlen und Wurzeln: Üblicherweise führt man C als Körpererweiterung von R zur Lösung beliebiger quadratischer Gleichungen ein. Das ist algebraisch ganz interessant. Als Physiker (und Elektrotechniker) gibt es jedoch viel wichtigere Gründe, um sich mit C auseinanderzusetzen
@herrfessa
Ja die komplexen Zahlen vereinfachen viele Berechnungen:-)
https://de.m.wikibooks.org/wiki/Komplexe_Zahlen/_Anwendung_in_der_klassischen_Physik
Zwei Schwingungen sollen addiert werden.
Eine Möglichkeit zur Lösung dieses Problems besteht darin, dass man die umständlichen Additionstheoreme anwendet.
Eine elegantere Möglichkeit ist, dass man die beiden Schwingungen in die komplexe Ebene wirft und dort die Addition durchführt.
Die Wirklichkeit entspricht dann dem Realteil des komplexen Ergebnisses.
Ich finde die Vorstellung, dass man ein Problem in der komplexen Ebene löst und und das Ergebnis in die Wirklichkeit zurück transformiert, in dem man nur den Realteil betrachtet, mehr als cool.
Ich finde es immer wieder faszinierend, wie sehr gerade die „zweidimensionalen“ komplexen Zahlen die Algebra erst zu einer runden Sache machen.
Die Anschauliche Erklärung, warum das nicht in noch höheren Dimensionen funktioniert, hat mir an diesem Artikel besonders gut gefallen.
Dennoch bleibt die Faszination, was das besondere an der „geometrischen“ Dimension Zwei ist, dass gerade in dieser die „Algebra“ so gut funktioniert?
Nicht nur die menschliche Wahrnehmung bzw. das menschliche Gehirn bevorzugt zwei Dimensionen – weil man hier aus der perspektiv der dritten alles so gut überblicken kann (unsere Schwierigkeit mit der dritten Dimension zeigt ja schon der berühmte Zauberwürfel).
Nein auch aus Sicht der Algebra ist die Zweite eine besondere Dimension.
Sehr schön, die Descartes-Multiplikation kannte ich noch gar nicht. Hab‘ lange überlegt, warum der Winkel der Geraden g keine Rolle spielt, aber mit dem Strahlensatz wie später erklärt wird es klar.
Gibt es für’s Dividieren auch eine geometrisch Konstruktion? Sollte doch dann auch irgendwie gehen.
Mit sehr sanftem Übergang vom Gewohnten zum Neuen beschrieben bzw erklärt, schick!
Exakt dieselbe, Alderamin – wie auch *räusper* bereits im Text gesagt.
@Alderamin: Die Multiplikation von Descartes ist auch interessant, weil bis dahin geometrisch gegolten hat: Strecke * Strecke = Fläche. Seine Konstruktion war die erste (so weit ich weiß) nach der Zahl * Zahl = Zahl ist.
@rolak
Ups, überlesen… aber ja, geht, wie man sich am Beispiel überlegen kann.
@Alderamin
Ich habe mir die Multiplikation von Descartes so verinnerlicht.
Die Gerade h1 normiert die Gerade g mit 1.
Runderklappen im Bogen auf R bedeutet in unserem Beispiel eine Multiplikation mit 2.
Wenn ich von Punkt A auf R im Bogen runderklappe ist in R der Wert 2. Daraus folgt beim Runderklappen von B ein Wert von 6.
Sieht nach einer grafischen Abbildung aus 😉
Ich verstehe nur nicht so ganz, warum das in höheren Dimensionen nicht funktionieren sollte?
Es kommen doch einfach nur weitere Komponenten (Länge + Winkel) hinzu … die man gleichartig behandeln sollte und damit wieder in einem eindeutigen Vektor gleicher Dimension landet?
Die „Negation“ im 3D wäre dann also ein Vektor der im 3D Raum genau in die entgegengesetzte Richtung zeigt.
Ich vermute mal, wenn ich mir nur die ersten 2 Komponenten der beiden Vektoren anschaue, sollte es dann eine 2D-Negation geworden sein.
Wo hab ich hier einen Denk- oder Visualisierungsfehler?
Als unser mathelehrer uns das so erklärt hat, sind viele Groschen gleichzeitig gefallen, die jahrelang zuvor durch abstraktere Erklärungen verklemmt waren.
Mathematik anschaulich erklärt – besser geht es nicht.
@neurino, @fragender
Die Sache mit Negation = Drehung um 180° und geht nicht in 3D und höher ist tatsächlich nur ein Plausibilitätsargument.
Dass es Divisionsalgebren nur in Dimension 1, 2, 4, und 8 gibt, hat bisher niemand algebraisch beweisen können. Die Beweise beruhen alle auf topologischen Argumenten (s. auch den entsprechenden Wikipedia-Artikel). Das ist jedenfalls nichts, was man einem Schüler (oder sonstigen Laien) so nebenbei erklären könnte.
Das ist aus meiner Sicht die beste Heranführung an komplexe Zahlen, um Schüler nicht gleich am Anfang zu verwirren, sondern zu interessieren.
Sehr gute Arbeit! Danke!
@herrfessa,
jaja da waren noch die Divisionsalgebren in Dimension 4 und 8. (Dimension 1 sind die Reellen Zahlen, Dimension 2 die Komplexen Zahlen)
@fragender:
Man kann wie von Dir beschrieben in jeder Dimension eine Addition und zugehörige Subtraktion -und damit auch Negation- definieren. (Das nennt sich Vektorrechnung.)
Das Problem ist, eine Multiplikation zu finden, zu der es auch eine passende Division gibt (sogen. Divisionsalgebren).
Außerdem erwarten man von seiner Addition und Multiplikation, dass sie einige einfache Grundeigenschaften erfüllen, damit man damit „vernünftig“ rechnen kann.
Man fordert z.B. dass A x B = B x A
oder dass A x (B + C) = A x B + A x B
sogen. Ausmiltiplizieren von Klammern
Solche grundlegenden Eigenschaften gehen in Dimension 4 und 8 schrittweise verloren,
so dass für die „richtige“ Algebra vor allem die 2 dim. Komplexen Zahlen und natürlich die 1 dim. Reellen von Interesse sind.
Gleiches gilt für Anwednungen in Elektrotechnik etc.
Die beiden höheren Dimensionen sind eher was für die „gute alte Topologie“, die rauszufinden versucht, was noch alles geht, und die sogar beweisen kann, dass Multiplikation mit Division in anderen Dimensionen überhaupt nicht möglich sind (das muss man erst mal hinkriegen).
@ herrfressa
Noch mal ein großes Kompliment für die wirklich anschauliche Darstellung dieses „komplexen“(!!!) Themas.
@neurino
Ich weiss ich oute mich jetzt wieder als Vollpfosten
.
mul und div sind ja auch nur wiederholte add und sub. Also dass Proplem liegt darin das es in den höheren Dimensionen keine gültige Algebra gibt. Hab ich dass so einigermahsen richtig verstanden?
@tomtoo
Multiplikation ist nicht gleich Multiplikation.
Kennst die russische Bauernmultiplikation ?
😉 🙂
@tomtoo
Die Anschauung von Multiplikatiin und Division als wiederholte Addition und Subtraktion haben wir von den reellen Zahlen
Also 2 x A = A + A etc.
Das geht auch noch wenn wir eine reelle Zahl (z.B. „2“) mit einer komplexen Zahl (a+ib) multiplizieren
z.B.: 2 x (a+ib) = 2a + 2ib = (a + ib) + ( a + ib)
Aber wenn wir zwei komplexe Zahlen mit einander multiplizieren dann müssen wir ausmultiplizieren
z.B. (2 + 3i) x (a + ib) = 2a + 2ib + 3ia – 3b(!)
Da funktioniert die einfache Anschauung mit der Adition nicht mehr so ganz. Da kommt dann die Anschauung mit der Derhung ins Spiel die in diesem Artikel so toll beschreiben ist.
Wirklich guter Beitrag, mit Text und Bild didaktisch perfekt aufgebaut, verständliche Sprache.
Gerade für Leute, die eher zu „bildhaftem Denken“ neigen, ist die Darstellung der Zahlenwerte als bewegliche (anwachsend und sich drehend) „Teile“ sehr verständnisfördend.
Wenn diese Darstellungweise eine eigene Erfindung des Autors ist, was mir nicht ganz klar ist, dann ist das Spitze!
@nourino
Danke ! Eben hatts click gemacht .
@Withold Ch.
Auf diese Art und Weise habe ich es sonst nirgends gesehen. Was aber nicht heißt, dass es andere nicht schon vorher gemacht haben.
Einer der ersten, der über die geometrische Interpretation der komplexen Zahlen geschrieben hat, war Caspar Wessel.
Richard Feynman hat in der 2. Robb Memorial Lecture (ab etwa 1:10:50; diese Lectures wurden dann das Buch QED) eine etwas andere geometrische Interpretation gebracht.
@nourino
Kleiner Nachtrag Thilo hatte so einen Beitrag über Hamilton also hab ich das Netz bemüht also die Biographie. Und das mit seinem Multiplikationsproplem das ihn wohl so lange umtrieb nicht verstanden. Jetzt ist das schon klarer
@ tomtoo
Freut mich sehr!
Für alle:
tomtoo hat mich auf einen interessanten Artikel gebracht der in diesem Blog erwähnenswert ist:
https://didaktik.mathematik.hu-berlin.de/files/2011_quaternionen.pdf
Dieser zeigt, dass Quaternionen (die vier dimensionale Erweiterung der Komlexen Zahlen) eine direkte Anwendung in der heutigen PROGRAMMIERUNG VON COMZUTERSPIELEN haben,
weil man damit DREHBEWEGUNGEN IM RAUM effizient darstellen kann.
Ich finde das ist eine starke Anwendung und ein weiteres Beispiel, wie eine mathematisch-theoritische „Spielerei“ viele Jahre später in der Praxis ankommen kann.
Der Beitrag von @herrfessa ist eine ideale anschauliche Grundlage dafür.
@tomtoo
vielen Dank für den Hinweis