Der Mond ist immer ein schöner Anblick am Himmel. Bei ihm gibt es immer was zu sehen. Mal ist Vollmond, dann Halbmond; mal ist er groß am Himmel zu sehen, mal untertags und mal gar nicht. Mal schiebt er sich vor die Sonne und mal wird er selbst ganz dunkel. Diese Dynamik in seinem Anblick wird von der komplexen Bewegung unseres Satelliten verursacht. Grund genug, sich der Bewegung des Mondes in einer eigenen Folge der Sternengeschichten zu widmen.
Und wie immer gibt es weiter unten eine Transkription des Podcasts.
Die Folge könnt ihr euch hier direkt als YouTube-Video ansehen oder direkt runterladen.
Den Podcast könnt ihr unter
abonnieren beziehungsweise auch bei Bitlove via Torrent beziehen.
Am einfachsten ist es, wenn ihr euch die „Sternengeschichten-App“ fürs Handy runterladet und den Podcast damit anhört.
Die Sternengeschichten gibts natürlich auch bei iTunes (wo ich mich immer über Rezensionen und Bewertungen freue) und alle Infos und Links zu den vergangenen Folgen findet ihr unter https://www.sternengeschichten.org.
Und natürlich gibt es die Sternengeschichten auch bei Facebook und bei Twitter.
Transkription
Sternengeschichten Folge 189: Die Bewegung des Mondes
Der Mond bewegt sich. So viel ist klar. Aber die Details sind knifflig und äußerst interessant. Der Mond bewegt sich um die Erde herum; das wusste man schon immer. Was man erst so richtig im 17. Jahrhundert verstanden hat war allerdings die Tatsache, dass das beim Mond tatsächlich etwas Besonderes ist. Bis dahin war man ja der Meinung, alle Himmelskörper würden sich um die Erde bewegen; nicht nur der Mond. Der Mond bewegt sich natürlich auch mit der Erde gemeinsam um die Sonne. All das macht seine Bewegung ziemlich kompliziert.
Der Mond braucht für eine Runde um die Erde ungefähr einen Monat. Das ist kein Zufall – unser Kalender basiert einerseits auf der Bewegung der Erde um die Sonne, andererseits aber auch auf der Bewegung des Mondes um die Erde und die Einteilung des Jahres in Monate stammt genau daher. Heute ist die Dauer eines Monats – aus historischen Gründen vergleichsweise willkürlich – auf 28, 29, 30 oder 31 Tage festgelegt. Die reale astronomische Dauer unterscheidet sich davon. Und es gibt auch mehr als nur eine Art, einen Monat zu definieren.

Da gibt es den siderischen Monat. So bezeichnet man den Zeitraum der vergeht, bis der Mond von der Erde aus gesehen in Bezug auf den als unveränderlich angenommenen Sternenhimmel wieder die gleiche Position am Himmel erreicht hat. Er beträgt 27 Tage, 7 Stunden, 43 Minuten und 11,6 Sekunden. Das ist kürzer als der synodische Monat, der in Bezug auf die Position der Sonne gemessen wird. Denn hier muss man auch die Bewegung der Erde um die Sonne berücksichtigen. Während ein siderischer Monat vergeht, bewegt sich auch die Erde ein Stück um die Sonne herum. Der Mond muss sich dann also noch ein wenig weiterbewegen, um diese veränderte Position in Bezug auf die Sonne auszugleichen und wieder genau so zu stehen wie zuvor. Das braucht knapp 2 Tage weswegen der synodische Monat insgesamt 29 Tage 12 Stunden 44 Minuten und 2,9 Sekunden dauert.
Da die relative Position von Sonne, Mond und Erde auch bestimmt, welche Mondphasen wir sehen können, ist das auch der Zeitraum, während der alle Mondphasen von Neumond über Halbmond bis Vollmond und wieder zurück zum Neumond durchlaufen werden. Beziehungsweise es ist fast der Zeitraum, denn der Mond folgt keiner exakten Kreisbahn um die Erde. Seine Bahn ist leicht elliptisch und nach dem zweiten Keplerschen Gesetz bewegt er sich unterschiedlich schnell je nachdem ob er der Erde ferner oder näher ist. Gravitative Störungen der anderen Planeten verändern die Bahn während längerer Zeiträume zusätzlich, so dass die Zeit zwischen zwei Neumonden nicht immer gleich lang ist. Die durchschnittliche Lunation, wie ein kompletter Durchlauf aller Mondphasen genannt wird, dauert 29,53 Tage.
Neben Lunation, synodischem und siderischem Monat hat die Astronomie noch drei weitere Monate parat. Da wäre der anomalistische Monat. Das ist die Zeit, die der Mond von Apogäum zu Apogäum beziehungsweise Perigäum und Perigäum braucht. Also die Zeit zwischen zwei Durchgängen durch den erdfernsten beziehungsweise erdnächsten Punkt der Mondbahn. Die Lage dieser Punkte ändert sich ebenfalls im Laufe der Zeit. Einmal in 8,85 Jahren dreht sich die Mondbahn einmal um die Erde herum. Grund dafür sind wieder die gravitativen Störungen der anderen Planeten. Der erdnächste und erdfernste Punkte bewegen sich dabei in der gleichen Richtung wie der Mond selbst und der anomalistische Monat ist deswegen ebenfalls ein wenig länger als der siderische Monat. Es braucht aber hier nur ein paar Stunden, bis der Mond die Drehung seiner Bahn ausgeglichen hat und der anomalistische Monat dauert daher 27 Tage, 13 Stunden, 18 Minuten und 33,1 Sekunden.
Neben Perigäum und Apogäum gibt es zwei weitere wichtige Punkte auf der Umlaufbahn des Mondes. Nämlich die Punkte, in denen sie die Umlaufbahn der Erde um die Sonne schneidet. Die Bahn des Mondes ist um wenig mehr als 5 Grad gegenüber der Erdbahn geneigt und die beiden Schnittpunkte werden in der Astronomie Knotenpunkte oder auch Drachenpunkte genannt. Der Name bezieht sich auf den alten Mythos des Drachen, der den Mond oder die Sonne verschluckt, wenn eine Finsternis stattfindet. Denn Mond- oder Sonnenfinsternisse kann es nur geben, wenn der Mond genau in oder zumindest in unmittelbarer Nähe von einem der beiden Schnittpunkt steht. Nur dann können sich Sonne, Mond und Erde in einer Linie befinden und einander so verdecken, dass entweder Mond oder Sonne verdunkelt werden.
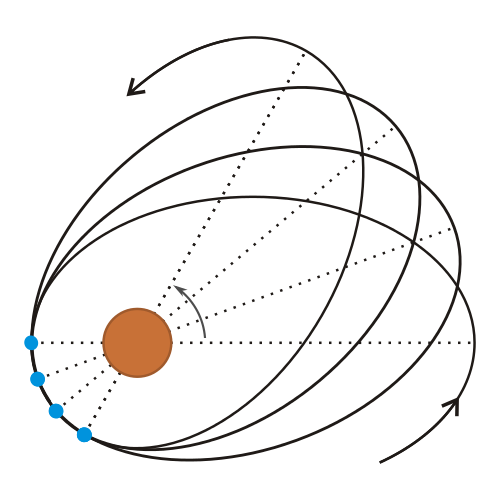
So wie Apogäum und Perigäum sind auch die beiden Knotenpunkte nicht fix, sondern verändern im Laufe der Zeit ihre Lage. Diesmal aber entgegengesetzt zur Bewegungsrichtung des Mondes, weswegen ein Umlauf des Mondes von Knotenpunkt zu Knotenpunkt ein wenig kürzer als ein siderischer Monat ist. Ein sogenannter drakonitischer Monat dauert 27 Tage, 5 Stunden, 5 Minuten und 35,9 Sekunden.
Als letztes gibt es dann noch den tropischen Monat. Hier wird die Position des Mondes auf den Frühlingspunkt bezogen, also den Schnittpunkt zwischen der Ebene der Erdbahn und dem Himmelsäqutor, also den auf den Himmel projizierten Äquators der Erde. Würde die Erdachse genau senkrecht auf die Umlaufbahn der Erde stehen, wäre diese identisch mit der Ebene des Himmelsäquators. Die Rotationsachse unseres Planeten ist aber um 23,5 Grad aus der Senkrechten geneigt. Meistens zumindest, denn auch dieser Winkel schwankt im Laufe der Zeit. Darum bewegt sich auch der Frühlingspunkt und zwar entgegen der Bewegungsrichtung von Erde und Mond. Der Zeitraum zwischen zwei Durchgängen des Mondes in Bezug auf den Frühlingspunkt ist also ebenfalls ein wenig kürzer als der siderische Monat. Allerdings nur um ein paar Sekunden, er dauert 27 Tage, 7 Stunden 43 Minuten und 4,7 Sekunden.
Aber all diese Genauigkeit und die Angabe auf den Bruchteil einer Sekunde genau ist eigentlich sowieso hinfällig. Die Erd- und auch die Mondbahn sind durch die gravitativen Störungen der anderen Planeten ständigen Veränderungen unterworfen. Ein Monat ist also genaugenommen niemals exakt gleich lang wie der vorhergehende und die verschiedenen Schwankungen können, je nachdem wie sie gerade zusammenspielen, durchaus auch Unterschiede von mehreren Stunden verursachen. Trotzdem lässt sich mit den annähernden Werten der verschiedenen Monate durchaus einiges anfangen.
Der griechische Astronom Meton hat im fünften Jahrhundert vor Christus zum Beispiel den heute nach ihm benannten Meton-Zyklus entdeckt. Zumindest vermutet man das, die historischen Quellen sind dürftig. Jedenfalls hat man irgendwann festgestellt, dass ein durchschnittliches Jahr, also ein Umlauf der Erde um die Sonne, 365,25 Tage dauert. Ein synodischer Monat dauert, wie vorhin erklärt, 29,53 Tage. Rechnet man ein wenig herum, dann findet man heraus, dass 19 Jahre mit 6939,75 Tage fast genau so lange dauern wie 235 synodische Monate mit 6939,55 Tage. Alle 6940 Tage wiederholt sich also eine bestimmte Konstellation zwischen Sonne, Erde und Mond. Und da ein synodischer Monat der Zeitraum ist, der den Wechsel der Mondphasen beschreibt, findet eine Mondphase – zum Beispiel Vollmond – die in einem Jahr an einem bestimmten Tag stattgefunden hat, 6940 Tage oder 19 Jahre später wieder am selben Tag des Jahres statt.

Neben dem Meton-Zyklus, der sich mit den Mondphasen beschäftigt, gibt es natürlich auch noch entsprechende Zyklen für die Abläufe von Mond- oder Sonnenfinsternisse. Die Sache mit den Finsternissen ist allerdings wirklich komplex. Ein wenig habe ich schon in Folge 57 der Sternengeschichten erzählt. Kurz zusammengefasst: Sonne oder Mond können sich nur dann verfinstern, wenn sie exakt in einer Linie mit der Erde stehen. Das kann nur passieren, wenn der Mond gerade in unmittelbarer Nähe eines der beiden Knotenpunkte steht. Außerdem muss dann aber auch noch gerade Voll- oder Neumond herrschen. Ist Vollmond, dann steht die Erde genau zwischen Mond und Sonne und der Erdschatten verdunkelt den Mond. Ist Neumond, dann steht der Mond zwischen Sonne und Erde und es gibt eine Sonnenfinsternis. Wie schon gesagt verändert sich die Position der Knotenpunkte aber im Laufe der Zeit. Steht der Mond in einem Jahr an einem bestimmten Tag im Knotenpunkt und gibt es eine Finsternis, dann erreicht der Mond im folgenden Jahr den Knotenpunkt schon 10 Tage früher. Dann passt die Konstellation nicht mehr so ganz und es wird eventuell keine Finsternis mehr geben, höchstens noch eine partielle Bedeckung. Man kann wieder das gleiche Rechenspiel anstellen wie beim Meton-Zyklus. 242 drakonitische Monate, die ja in Bezug auf die Knotenpunkte gemessen werden sind ziemlich genau gleich lang wie 223 synodische Monate die die Mondphasen beschreiben. Dieser Zeitraum entspricht 18 Jahren und 11,3 Tagen und so lange dauert es, bis der Mond nicht nur wieder die selbe Position in Bezug auf Sonne und Erde sondern auch zum Knotenpunkt einnimmt.
Sonnen- und Mondfinsternisse wiederholen sich also nach 18 Jahren und 11,3 Tagen und diese Periode, die auch Saros-Zyklus genannt wird, wurde schon im Altertum bei den Babyloniern zur Vorhersage von Finternissen benutzt. Sie stimmt allerdings nicht exakt; all die verschiedenen Störungen, Schwankungen und anderen Variationen führen zu Abweichungen. Und über die Mondbahn selbst gäbe es auch noch jede Menge zu sagen. Aber das hebe ich mir für eine andere Folge der Sternengeschichten auf…

„Das braucht knapp 2 Tage weswegen der synodische Monat insgesamt 29 Tage 12 Stunden 44 Minuten und 2,9 Sekunden dauert.“
29d 12h (synodischer Umlauf, steht oben)
-27d 7h (siderischer Umlauf, steht oben)
= 2d 5h (Differenz) sind nicht „knapp 2 Tage“
sondern gut 2 Tage. Oder hab ich da irgendwas falsch verstanden
@Jürgen: Ja, nämlich das „knapp“ in anderen deutschsprachigen Ländern nicht das gleiche bedeuten muss wie in Deutschland…
Asteroidenwitze… schon nerdig, das muß man sagen. Aber gut, einen habe ich:
Ein Asteroid zum anderen: „Nimmt einen doch immer wieder mit, so eine AGB-Phase“.
Das verstehe ich nicht ganz. Finsternisse entstehen, wenn der Mond aus Sicht der Sonne vor oder hinter der Erde steht. Aber die Schnittpunkte von Mond- und Erdumlaufbahn befinden doch aus Sicht der Sonne rechts und links neben der Erde.
An den Punkten, an denen der Mond die Erdbahn schneidet, müsste seine Position ca. 90 Grad von der Sonne entfernt und er für uns als Halbmond zu sehen sein.
Warum erscheint mir das Bild, das der Artikel schildert, um 90 Grad verdreht? Habe ich irgendwas übersehen?
@Dampier:
Ja. Den Satz unmittelbar unter dem Bild:
„So wie Apogäum und Perigäum sind auch die beiden Knotenpunkte nicht fix, sondern verändern im Laufe der Zeit ihre Lage. „
Die Halbachsen der Mondbahn drehen sich halt auch – und mit ihnen die Drachenpunkte.
Wie kann ein Schnittpunkt von Mond- und Erdbahn zwischen Erde und Sonne liegen?
moin Dampier, die so phantasievoll benannten Drachenpunkte sind die Schnittpunkte von Mondbahn und (Erd)Ekliptik – und sowas kann schon mal zwischen Erde und Sonne liegen.
@rolak, danke, jetzt ergibt es Sinn. Im Artikel steht „Bahn“, das ist etwas irreführend.
@rolak:
Danke für die Präzisierung.
@Dampier:
Schon gleich nachdem ich das abgeschickt hatte war mir klar, dass ich das zu ungenau formuliert hab. Aber @rolak hats ja klar gemacht …
@ FF
Entschuldigung, daß ich das Wörtchen „knapp“ falsch interpretiert habe. Ich werde also künftig, wenn meine Frau sagen sollte „Die Hose ist aber knapp !“ erstaunt fragen „Wieso, die Hose schlampert doch gar nicht an mir herum. Die sitzt doch angegossen, wie ’ne Wurstpelle !“
Florian, für die Menschen in deinem jetzigen Umkreis (Jena, Thüringen) bedeutet knapp, etwas weniger als. Und das ist auch für die meisten anderen deutschsprachigen Menschen so. Und auch für die meisten nicht deutschsprachigen Menschen ist das so, weil auch im Wörterbuch (Langenscheidt: Neues Großwörtebuch Englisch) nur die Bedeutung „Etwas weniger als / zu wenig“ (mit Abwandlungen) steht. ein ungefähr gibt es da nicht.
Florian, ich bin kein Krümelkacker, mir gefällt dein Artikel auch so sehr gut. Ich wollte dich nur auf das ungewöhnliche Gefühl aufmerksam machen, was viele Menschen haben, wenn sie das lesen.
@Jürgen: „Florian, für die Menschen in deinem jetzigen Umkreis (Jena, Thüringen) bedeutet knapp, etwas weniger als.“
Ich kommuniziere nicht ausschließlich mit und für Thüringer. Wir können ja abstimmen lassen, welche Wörter ich verwenden darf und welche nicht. Und wenn ich dann mit knapper Mehrheit gewonnen habe – habe ich dann „etwas weniger als“ die für eine Mehrheit nötigen Stimmen bekommen oder nicht?
Ist eigentlich die Gravitationskraft die der Mond auf die Erde ausübt auch etwas abhängig von der Mondphase ?
Der 25h Umlauf des Mondes verursacht die Gezeiten – klar ! Aber müsste der Gezeitenhub bei Neumond nicht etwas stärker sein ?
Schliesslich müssten sich ja die Anziehungskräfte von Mond und Sonne bei Neumond addieren …
@ATC
Nein, Ja, Ja
@Franz:
verstehe ich jetzt nicht ganz…..
Mondphasen spiegeln doch die Positionsverhältnisse von Sonne, Erde, Mond wieder.
@A.T.C:
Genau. Deshalb die zwei ‚ja‘ von @Franz.
Bei Neumond und bei Vollmond, wenn Sonne, Mond und Erde in einer Linie stehen, ist der Gezeitenhub geringfügig höher als im Mittel: Springtide.
Das „Gegenteil“ ist die Nipptide.
Was die Gravitationswirkung des Mondes angeht, ist die Antwort von Franz nur in erster Näherung richtig.
Auch die Umlaufbahn des Mondes um die Erde ist ja nicht kreisförmig sondern eine Ellipse. Dh. mal ist der Abstand Mond / Erde geringfügig grösser, mal kleiner. Da die Anziehung zwischen den Beiden nur von der Masse und dem Abstand abhängt, ist damit auch die Gravitationswirkung des Mondes auf die Erde unterschiedlich. Der Unterschied ist allerdings nicht sehr groß.
Du kannst den Unterschied mal Spasseshalber selber nachrechnen, in dem du dir aus dem Wikipedia-Artikel über den Mond die kleinste und grösste Entfernung Erde-Mond raus suchst und die beiden Werte in die bekannte Gleichung für die Gravitationskraft einsetzt:
F = G * m1 * m2 / r^2
Du wirst sehen, dass der Unterschied so klein ist, das man Franz ohne Weiteres recht geben kann …
Danke für den Link.
Eine gute Darstellung habe ich auch hier gefunden:
https://en.wikipedia.org/wiki/Tide#/media/File:Tide_schematic
https://en.wikipedia.org/wiki/Tide#/media/File:Tidalwaves1.gif
@PDP10, ATC
Sorry für die kurze Antwort, hatte grad keine Zeit 🙂
Ist eigentlich die Gravitationskraft die der Mond auf die Erde ausübt auch etwas abhängig von der Mondphase ?
Diese Frage kann man IMO aus zwei Blickwinkeln sehen. Es gibt keinen ursächlichen Zusammenhang zwischen Mondphase und Gravitation, da Gravitation nur von Masse und Entfernung abhängt und die Mondphase aus dem Beleuchtungswinkel der Sonne entsteht. Es entsteht aber ein scheinbarer Zusammenhang weil sich Sonnengravitation und Mondgravitation in verschiedener Stärke addieren bei verschiedenen Mondphasen.
By the way, wie war die Frage gemeint ?
@Franz
Frage war so gemeint:
Ist die Spring-Tide bei Neumond (für einen normalen Beobachter) stärker als bei Voll-Mond ?
https://de.wikipedia.org/wiki/Gezeiten#.C3.9Cberlagerung_der_vom_Mond_und_von_der_Sonne_verursachten_Gezeitenkr.C3.A4fte
Hier zb. lautet es:
In der oben genannten Periode von etwa 29½ Tagen liegen Sonne, Erde und Mond zweimal auf einer Linie und die von ihnen verursachten Gezeitenkräfte addieren sich…..
Kann das stimmen ? Das liest sich so als würde bei Vollmond (genauso wie bei Neumond) die Gravitationskraft des Mondes sich mit der, der Sonne addieren.
@Franz:
Exakt. So wollte ich das sagen, habs aber ein wenig zu allgemein aufgefasst.
Es ist ja so: Da die grosse und kleine Halbachsen der Mondbahn selber präzessieren, fällt manchmal der kleinste Abstand Mond-Erde zB mit dem Vollmond zusammen. Manchmal aber auch mit dem Neumond.
@A.T.C:
Jein. Das würde man intuitiv annehmen. Das ist aber nicht so einfach, weil da nicht die einfache Anziehung zwischen den beiden Körpern die Hauptsache ausmacht, sondern die Gezeitenkräfte die deutlich unintuitiver zu verstehen sind.
Such mal hier im Blog nach dem Stichwort. Florian hat gerade zu diesem Thema einige sehr anschauliche Artikel geschrieben.
@A.T.C.:
Das ist auch so. (dein Post hat sich mit meiner Antwort auf den vorherigen überschnitten)
Siehe oben.
@PDP10
Ergänzung: Dies dauert über 18 Jahre. Aber bereits innerhalb eines Jahres wandert die Position des Vollmondes (wie auch aller anderen Mondphasen) einmal um die Mondbahn herum, weil Erde und Mond die Sonne umkreisen. Haben wir etwa im Herbst einen „Super-Vollmond“ in Erdnähe, so haben wir Frühjahr entsprechend einen „Mini-Vollmond“ in Erdferne. Die Drehung der Mondbahn sorgt dafür, dass sich diese Zeitpunkte allmählich ändern und in 18,3 Jahren einmal um das Jahr herum verschieben.
@A.T.C
Zur Frage „Ist die Springtide bei Neumond stärker als bei Vollmond?“
Zur Antwort kommt man, indem man sich die Gezeitenentstehung noch mal anschaut: Der Flutberg in Richtung des Mondes entsteht dadurch, dass die Oberfläche dort stärker vom Mond angezogen wird als der Erdmittelpunkt. Der Flutberg in der anderen Richtung entsteht dadurch, dass die Oberfläche weniger stark angezogen wird als der Erdmittelpunkt. Diese Differenzen der Anziehungskraft sind zwar nicht exakt identisch, aber der Unterschied ist so gering, dass er praktisch unmerklich ist.
Die von der Sonne erzeugten Gezeiten funktionieren ähnlich, hier ist der Unterschied zwischen sonnenzugewandter und abgewandter Seite noch geringer.
Bei der Überlagerung von Mond- und Sonnengezeiten dominiert klar der Mond, so dass es zu Springtiden kommt, wenn die Flutbergkomponenten sich überlagern, und zu Nipptiden, wenn sie im rechten Winkel zueinander stehen.
Wenn man arg theoretisch ist, könnte man sagen, dass die Flut in Richtung von Sonne und Mond bei Neumond die größte ist, gefolgt von der in Richtung des Mondes bei Vollmond, gefolgt von der in Richtung der Sonne bei Vollmond, gefolgt von der gegen Sonne und Mond bei Neumond… die Unterschiede dürften aber unterhalb des Messfehlers liegen.
@Ambivalent
Zumal die Neigung der Erdachse und die Topologie der Kontinente und Kontinentalschelfe ohnehin dafür sorgen, dass von den beiden theoretischen Flutbergen in der Praxis nicht viel übrig bleibt…
Mal ne Frage: Die Distanz des Mondes beeinflusst die Gezeiten des Meeres auf der Erde und auch ihre Intensität.
Ein kleiner Meteorit der Mond trifft beeinflusst nun nicht relevant dessen Bahn und Abstand zur Erde und damit Gezeiten.
Meine Frage bezieht sich nun auf ein Szenario mit einem so großen Asteroiden, der zwar die Erde verfehlt aber einen Volltreffer auf dem Mond landet der so stark ist, dass es Rückwirkungen auf dessen Bahn und samit Abstand zur Erde und der Intensität der Gezeiten hätte.
Die Frage bezieht sich also darauf ob es hier grundsätzliche Denkfehler gibt oder das grundsätzlich so vorkommen könnte und eine ganz grobe Einschätzung um was für eine Größe des Asteroiden es sich da handeln müsste.
Kann das so funktionieren, wie sähe der Mond nach so einer gigantischen Kollision optisch im Sonnenlicht von der Erde aus, also alles so ungefähre Einschätzungen aber eben mit einem Hintergrund aus Fachwissen, das ich so nicht habe. Danke.
@Bumms: „und eine ganz grobe Einschätzung um was für eine Größe des Asteroiden es sich da handeln müsste.“
Damit sich die Bahn des Mondes maßgeblich ändert, muss man da mindestens etwas drauf schmeißen, dass annähernd so groß wie der Mond selbst ist. Also eher unwahrscheinlich…
@Bumms
Ich (Laie) glaube, ein Asteroid von der Größe würde Stücke aus dem Mond heraussprengen, die dann drohen, auf der Erde einzuschlagen. Eine Veränderung der Gezeiten wäre dann wohl das weitaus geringere Problem.
Schöne „what if“-Frage. Bin gespannt, was die Fachleute sagen …
@PDP10 (#5, #9) Danke für deine Antworten! (hatte ich völlig vergessen, sorry. Ist eigentlich nicht meine Art, jemanden wortlos stehenzulassen ;))
Ja danke schon mal für die Antworten bisher, klar wäre das unwahrscheinlich, ich dachte nur mal dass sowas ein Szenario ist, über das ich eigentlich noch nie was von fachlicher Seite gelesen habe, es geht immer nur um Einschläge auf der Erde und so apokalyptische Megakatastrophen im Zusammenhang mit Asteroiden, aber was wäre eben wenns mal den Mond trifft und es so „mittelmässige“ Auswirkungen gäbe, also sagen wir mal einfach durchschnittlich maximal eine Verdopplung der Gezeitenhöhen, oder Verdreifachung. Da würde es schon ziemlich brausen auf den Meeren, die Menschheit aber existiert weiter mit jedoch plötzlich ganz neuen Herausforderungen u.a. im Welthandel etc.
Ich fand das eine spannende neue Überlegung, eben in dem Fall dass es gerade NICHT ein total apokalyptisches „Alles-aus-Szenario“ wäre und weil es eben diesmal um den Mond ginge. Schlägt etwas auf dem Mars ein, kanns uns ja egal sein und wenn es auf der Erde in großem Stil einschlägt ist finito, aber mein Gedanke war eben, was ist beim Mond und wie wären da die Größenordnungen.
Dass das Ding so groß sein müsste wie der Mond selbst erstaunt mich nun sehr, weil es mir ja gerade nicht um eine solche „Alles aus Katastrophe“ geht wo es den Mond zerreißt und uns um die Ohren haut, sondern es geht mir um eine Einschätzung wie wenn man die Massen sagen wir mal ausgehend vom Tscheljabinsker Ding weiter steigern würde, bis man zur ersten Mal sagen wir auch nur eine Gezeitenerhöhung von 1 m feststellen kann. Klar kann man das nicht exakt umrechnen auf eine Größes des Asteroiden aber es überrascht mich wenn ich lese dass erst bei fast gleicher Größe wie der Mond da sich was täte, wahrscheinlich liegt es aber auch daran, was man unter dem Begriff „massgeblich“ hier versteht. Mir geht es wie gesagt um eine Annnäherung an eine Größenordnung wo es zuerst mal nur eine ganz leichte aber dennoch klar messbare Zunahme der Gezeitenhöhen käme und eben dann davon ausgehend den Bereich, in dem die Menschheit durchaus noch weiterexsitieren, aber auf die Veränderung reagieren müßte…..
@Bumms: „Dass das Ding so groß sein müsste wie der Mond selbst erstaunt mich nun sehr“
Stell es dir so vor: Was müsste ich auf dich werfen, damit du umfällst? Ne Erbse? Nen Apfel? Eine Wassermelone? Einen Autoreifen? Ein Auto? Du hast ne Masse und für dich gilt – so wie für den Mond – das 1. Newtonsche Axion: Du willst deinen Bewegungszustand nicht ändert. Es gilt auch das zweite: Wenn du den Bewegungszustand ändern willst, brauchst du eine Kraft. Eine Kraft ist Masse mal Beschleunigung. Um dich umzuschmeißen brauche ich also etwas mit ausreichend Masse. (Oder etwas das enorm schnell ist – das sind Asteroiden aber nicht; zumindest wenns um Mondzerstörung geht).
@Florian
Ja genau, so hab ich mir das auch gedacht, nur dass es viel eher mit „schwimmend“ gelagerten Massen zu vergleichen wären die ihre Richtung ändern und nicht mit einem „umwerfen“.
Man weiß ja wie bei einem Schiff mit sehr großer Masse ein an einem Seil ziehender Mensch mit sehr kleiner Masse durchaus etwas bewirken kann, stellt man das Schiff dagegen an Land versauen die Reibungskräfte einem alles.
Im All gibt es aber keine solchen Reibungskräfte und deshalb hab ich den Einfluss einer relativ kleinen Masse hier schon viel höher eingeschätzt. Man stelle sich also mal ein Menschlein vor, das sich mit einem Ruck ins Seil wirft oder vom Ufer in ein tonnenschweres Boot spring
Da ist dann nach meinem Verständnis schon eine sehr kleine Masse wie von einem 100 kg Mensch ausreichend ein viele Tonnen wiegendes Schiff messbar zu beeinflussen, bei einem Flugzeugträger merkt man natürlich nix in dem Fall.
Und bei der Mondbahn geht es ja auch nur um ein Eiern von einer gewissen Anzahl von Kilometern was schon messbare änderungen der Gezeitenhöhen ergibt, so riesig groß müsste der Impuls doch gar nicht sein, hm?
Na ja, OK, ich will nicht nerven, wenn aber noch interessante Vertiefungen dazu kommen, gerne.
@Bumms: „Im All gibt es aber keine solchen Reibungskräfte und deshalb hab ich den Einfluss einer relativ kleinen Masse hier schon viel höher eingeschätzt. „
Die relevante Größe ist der Impuls: Masse mal Geschwindigkeit. Und beim Mond hast du VIEL Masse die sich mit hoher Geschwindigkeit durchs All bewegt.
„Und bei der Mondbahn geht es ja auch nur um ein Eiern von einer gewissen Anzahl von Kilometern was schon messbare änderungen der Gezeitenhöhen ergibt, „
Ja? Ich kann mir nicht vorstellen, dass ein paar km Änderung der Mondbahn die Gezeiten messbar verändern. Der Mond ändert seinen Abstand zur Erde ja im Lauf eines Monats um ein paar zehntausend km (weil er einer elliptischen Bahn folgt). Außerdem entfernt er sich jedes Jahr 4cm von der Erde (wegen der Gezeitenreibung).
Nachtrag:
Gut dass Du auch die Geschwindigkeit erwähnt hat, wobei „nicht besonders schnell“ wohl eher beim „Überholen“ des Mondes gelten würde, bei „frontal entgegenkommend“ oder „von der Seite“ wären aber solche 20.000 km/h doch durchaus ein Faktor der die für eine messbare Wirkung benötigte Masse um einige Stellen vor dem Komma erniedrigen würde. Käme der Asteroid „von hinten“ mit was weiß ich nur 20.000 km/h so würde er den Mond mit seinen 3.600 km/h zwar auch ganz schön anboxen, aber eben um 20 % weniger als von der Seite kommend oder gar von vorne.
Gut dass Du die Geschwindigkeit erwähnt hast, also ich wüßte jetzt nicht warum bei einer solchen fünfstelligen Geschwindigkeit nicht auf der anderen Seite die für eine messbare Einwirkung benötigte Masse sich nicht ebenfalls mehrstellig ruduzieren sollte, gerade wegen den von Dir erwähnten Gleichungen.
Naja OK, ich hab mir mal ein erstes Bild machen können, besten Dank und ich schau gern mal wieder rein ob sich noch was ergeben hat….
Sorry, jetzt istz mir doch noch was Gutes eingefallen:
Also eine Gewehrkugel oder Schrotladung mit ihren 4000 km/h kann wie man zumindest in Filmen immer wieder sieht, einen Menschen durchaus „umwerfen“ und meines Wissens ist sowas zumindest bei einer Schrotladung auch durchaus realistisch.
Na da hätten wir dann doch eine Größenordnung, oder?
Ein Asteroid mit seinen ca. 20.000 km/h trifft den Mond mit seinen 3.600 km/h egal aus welcher Richtung in jedem Fall immer noch mit mehr als Projektilgeschwindigkeit.
Und ein Projektil mit seinen 5-30 Gramm kann einen ca. 500 Mal so schweren Menschen mit seinen 100 kg schon „ziemlich aus der Bahn werfen“, also OK, so kann ichs mir nun eigentlich vorstellen, falls da nicht ein entscheidender Denkfehler drin wäre….
@Bumms: „OK, so kann ichs mir nun eigentlich vorstellen, falls da nicht ein entscheidender Denkfehler drin wäre….“
Der Mond hat eine Masse von 70 Trilliarden Kilogramm! 22 Nullen hinter der 7…
@Bumms:
Kugeln durchschlagen einen Menschen, aber sie werfen ihn nicht um. Autos explodieren ja auch nicht, nur weil sie irgendwo gegengefahren oder abgestürzt sind.
Ich glaube dass ein Einschlag eines Asteroiden auf dem Mond für die Erde doch problematischer sein könnte. Und zwar aus einem anderen Grund:
Der Impakt könnte dermassen viel Gesteinsmaterial in den Weltraum schleudern, welches dann auf die Erde zutreibt. Selbst wenn die kleineren Brocken vermutlich nie die Erde selbst erreichen, so verdampfen diese doch in der Erdatmosphäre.
Das könnte zu einem thermischen Problem für die Erde werden.
Wie gross müsste ein derartiger Asteroid sein um solch einen Effekt auszulösen ?
@Bumms:
Wie @Captain E. schon angemerkt hat: Nein.
Die kinetische Energie ist winzig im Vergleich zur Energie die man aufwenden müsste um die träge Masse meines hier vor dem PC sitzenden Arsches auch nur einen Millimeter / s^2 zu beschleunigen.
Das gleiche gilt auch für Asteroid vs. Mr. Mond.
Was man in den Filmen sieht ist Unsinn.
Da gabs sogar mal eine Mythbusters Folge zu …
Oh, wer beim Militär war weiß, dass der Rückschlag eines Gewehrschusses ganz schön in die Schulter geht und blaue Flecken macht… Die Kraft muss nur über genügend Fläche verteilt werden, dann gibt’s kein Loch. (OT: mein Großonkel, der im Krieg war und angeschossen wurde, erzählte mir mal, getroffen zu werden fühle sich so an, als ob man von einem Stein getroffen würde; nur wird’s dann an der Stelle dann heiß und nass).
Aber die meisten Asteroiden sind ja weniger als 1 km groß, das macht natürlich im Vergleich zum Mond mit 3500 km Durchmesser (also größenordnungsmäßig der 3500³ = ca.40-Milliarden-fachen Masse) nicht viel aus. Einige sind ein paar 10 km groß, dann reden wir immer noch über ein Massenverhältnis von 1:mehrere Millionen. Das steckt der Mond locker weg.
Umgekehrt ist eine Methode, einen Asteroiden von bis zu 1 km auf Kollisionskurs mit Erde abzulenken, eine Raketenstufe mit ihm kollidieren zu lassen. Das lenkt den Asteroiden dann um Zentimeter/s von seiner Bahn ab, so dass er nach Jahren die Erde knapp verfehlt. Ein paar Tonnen Raketenstufe stören so einen Asteroiden nicht besonders. Einen 10 km durchmessenden schon gar nicht.
Wenn ein richtig großes Objekt auf dem Mond einschlagen würde (sagen wir mal: Ceres mit rund 1000 km Durchmesser und 1/40 Mondmasse), sähe das anders aus. Allerdings wäre die Chance groß, dass der Mond nicht zentral getroffen würde und ein Teil des Impulses in Drehimpuls umgesetzt würde. Außerdem gibt es nur eine Ceres, und nur eine handvoll Asteroiden ähnlicher Größenordnung im Asteroidengürtel (im Kuiper-Gürtel gibt’s allerdings viel mehr). Und keiner von denen kommt Erde und Mond nahe.
@Alderamin:
Wobei wir auch ganz entspannt bei Newtons 3. Gesetz gelandet wären (hätt mir auch früher als anschauliche Begründung einfallen können).
Wenn jemand im Film von einer Kugel getroffen wird und dann zwei Meter rückwärts durch die Gegend fliegt müsste dem Schützen nach Newton genau das gleich passieren … und nicht nur ein blauer Fleck an der Schulter …
OK, Will Smith passiert das mit seiner Mini-Wumme in MIB tatsächlich 🙂
Das ist aber auch das einzige mal, dass ich das in einem Film gesehen habe.
Wenn ein 80 kg schwerer Profi-Weitspringer mit 10 m/s anläuft, abspringt aber dann nicht in die Sandgrube sondern in KungFu-Manier gegen eine Stahltüre springen würde um sie aufzubrechen, ergibt das einen Schlag von 4 KiloJoule.
Wenn jedoch eine Nato-Scharfschützen- oder Maschinengewehrpatrone mit 12 mm Dicke und 10 cm Länge die 40 Gramm wiegt auf die Stahltüre geschossen wird, ergibt das laut zugerhöriger Tabelle eine Schlagenergie von 20 KJ, also so wie wenn 5 KungFu-Kämpfer gleichzeitig gegen die Türe springen.
Also manche hier scheinen das völlig zu unterschätzen.
Klar geht die durchs Fleisch durch bzw reißt ganze Löcher oder Körperteile ab, aber wenn diese Wucht absorbiert wird wie das beim Mond der Fall wäre, dann haut sowas einen Menschen definitiv um.
Und jetzt versuche ich mal die Mondgeschichte in die Relation zu setzen zu diesem Fall, wo so ein Projektil mit einer Wucht wie 5 fliegende KungFu-Kämpfer gleichzeitig einen Menschen definitiv umhaut.
40 Gramm gegenüber einem 100 kg Mensch macht den Faktor 250. Und die vierfache Geschindigkeit des Asteroid gegenüber der Kugel macht den Faktor 4, gibt zusammen den Faktor 1000 um den der Asteroid kleiner sein kann als der Mond bei gleichem Effekt.
Und wenn man sich sagt, wieso 5 KungFu-Kämpfer, einer reicht doch schon, dann wäre es der Faktor 5000.
Verdoppelt sich der Durchmesser einer Kugel (hier als geometrischer Körper), so verachtfacht sich die Masse.
Das bedeutet, dass wenn eine Asteroiden-Kugel mit dem 5000 sten Teil der Masse des Mondes ausreichen würde, so kann man mit dem Faktor 8 auf den Durchmesser umrechnen und das ergäbe dann ca die Zahl 600 .
Also eine geometrische Kugel mit dem 600-sten Teil des Durchmessers des Mondes würde wegen der riesigen Geschwindigkeit hier ausreichen um den Effekt zu erbringen als ob ein Karatekämpfer mit 80 kg und 10 m/s einen Mensch anspringt und umhaut.
Der Mond hat einen Durchmesser von sagen wir 3500 km und das durch 600 ergibt ca 6 km.
Also müßte ein Asteroid mit lediglich 6 km Durchmesser wegen seiner reisigen Geschwindigkeit ausreichen einen solchen Effekt auf den Mond auszuüben, als wenn ein 80 kg Karatekämpfer waagrecht in der Luft fliegend mit 10 m/s einen anderen Menschen anspringt und definitv damit „aus der Bahn wirft“.
Oder?
@Bumms: Nochmal: Der Mond hat eine Masse von 70 Trilliarden Kilogramm… ein 6km Asteroid ist dem völlig egal.
Oder hätte ich 250 nicht mit 4 und dann mit 5 multiplizieren dürfen sondern das addieren? Dann wäre es ein Asteroid mit ca. 100 km Durchmesser, na ja, dennoch praktikabel…..
@Bumms: Siehe auch hier: https://www.popsci.com/science/article/2013-07/could-asteroid-impact-knock-moon-earth
@ Florian
Meine Umrechnung hatte noch weitere Fehler, wie ich gemerkt habe und OK, ich gebs auf das Ding jetzt besonders klein rechnen zu wollen und lasse mich mal von Dir und dem Artikel überzeugen dass es ein großes Ding sein müßte.
Schön dass dort dann auch auf das Thema mit den Gezeiten eingegangen wurde.
Das klingt also dann so, als sei es grundsätzlich möglich den Kurs so zu verändern, dass die Gezeitenintensitäten sich verachtfachen.
Bestan Dank, damit gebe ich mich zufrieden, jetzt ist nur noch die Frage, wie sowas von der Erde aus aussehen würde. Ich nehme mal an, dass dies in jedem Fall soviel Material rausschleudern würde, dass es nachts vor lauter Sternschnuppen ein regelrechtes Feuerwerk am Nachthimmel gäbe, oder?
Würde es auf der Erde passieren, würde es zusätzlich die Atmosphäre und damit Sonne verdunkeln wie bei einem Vulkanausbruch, aber wie ist das wenn es im All passiert, dass soviel Staub und Zeug so in der Nähe der Erde hochgeschleudert würde, würde das auch die Sonne verdunkeln?
Und wie würde dann so ganz ungefähr der Mond aussehen, wenn er nach dem Hochschleudern all dieses Staubs und Materie von der Sonne angeleuchtet würde. Würde er da so weißlich wie bisher erscheinen und nur gedämpfter, oder würde das auch die Farbe verändern aus unserer Perspektive?
Wobei mir das Beispiel mit dem 4-jährigen in dem Artikel nicht gefällt, denn der NFL-Mann kann ja beim nächsten Schritt nach der Kollision mit der Masse des 4-jährigen sofort einen etwaigen seitlichen Impuls durch seine Fußstellung und Gewichtsverlagerung in den Boden ableiten, im All oder im Wasser bei einem Schiff geht sowas nicht, ein eingebrachter Impuls, eine eingebrachte Kraft wirkt hier viel besser und da kann doch die Masse eines Vierjährigen die Masse eines Erwachsenen durchaus beeinflussen. Wenn jetzt ein Erwachsener auf eine Schale spingt die auf dem Eis mit wenig Reibung schlittern kann, dann wird die sich mit ihm in die Richtung bewegen in die er aufgesprungen ist. Springt jetzt von der Seite auch nur ein Vierjähriger auf, dann muss das meiner Überzeugung nach einfach zu einer messbaren Bahnänderung führen und auch wenn man eine Kugel auf die Person schiessen würde.
Wenn keine Reibung im Spiel ist, kann ich mir einfach auch jetzt noch nicht vorstellen, wie auch ein relativ kleiner Impuls sich nicht doch in einer Bahnänderung auswirken soll. Wenn der große Körper anfangs nach vorne fliegt und es reibungsfrei und ohne dass die Kraft abgeleitet werden kann einen seitlichen Impuls gibt, muss es auch eine Bahnänderung geben. Und 15 kg gegenüber 100 kg ist hier einfach schon sehr viel, wenn es ohne Reibung und Ableitmöglichkeit seitlich einwirkt…..
@Bumms: Nochmal: Ja, es gibt eine Bahnänderung. Immer. Auch wenn ein Staubkorn auf den Mond fällt, ändert sich dadurch dessen Bahn. Aber du willst (warum eigentlich?) unbedingt beweisen, dass ein kleiner Asteroid eine relevante und auf der Erde merkbare Bahnänderung verursacht. Das passiert aber nicht. Weil die Physik nicht so funktioniert. Sondern eben laut den Newtonschen Gesetzen. Und da brauchst du eben eine große Masse, wenn du eine andere große Masse beeinflussen willst.
Ich fand einfach dass das ein bisher zu wenig beachtetes Thema ist und konnte dann mit der ersten Auskuft die Massen müßten gleich groß sein nichts anfangen, das weckte meinen Ehrgeiz. Dann las ich im Artikel „This orbital momentum is so great that it would overwhelm the impact force “
und dachte OK, Momentum?, vielleicht ja auch weil die Erde mit ihrer Schwerkraft weiter am Mond „zieht“ und es nicht nur so Bewegungen frei umherschwebender Körper sind…
Aber was solls, eine Abschätzung der Größe die ein „mittleres Ereignis“ bedeuten wird klappt wohl einfach nicht, für den Fall „gleich groß“ geht man im Artikel ja von einem Stopp des Mondes aus, für den Fall „Ceres“ geht man von fast keiner Reaktion aus und das mit einer Begründung die ich nicht nachvollziehen kann und dann wird der Fall einer relevanten Abweichung der Bahn doch noch erwähnt, aber im Fall welcher Größe zwischen „Ceres“ (minimale Ablenkung) und „gleichgroß“ (Stopp) kommt nicht so zum Ausdruck, dass es nachvollziehbar und die Herleitung verständlich wäre im Artikel.
Dennoch danke für die Mühe und Geduld, vielleicht befasst sich ja mal jemand speziell mit dieser Fragestellung so, dass man zum Beispiel für eine dreifache Gezeitenhöhe die zugehörige Bahnabweichung uind die zugehörige Asteroidenmasse konkret berechnet, dann gerne Hinweis an mich.
@Bumms:
Ähm, nein. „Momentum“ ist der Impuls (beliebter Fehler, den man als Physikstudent am Anfang immer wieder gerne macht).
Das heißt, das „orbital momentum“ ist der Bahndrehimpuls – nicht das Drehmoment …
Mit dem Impuls kannst du dir das aber vielleicht ein wenig klarer machen – es gilt ja die Impulserhaltung.
Lass uns mal annehmen, Ceres und Mond würden, jeweils mit gleicher Geschwindigkeit, aufeinander zu rasen. Ceres hat aber nur ungefähr ein Hundertstel der Masse des Mondes. Dh. ihr Impuls (p = m * v) ist in unserem Beispiel (gleiche Geschwindigkeit) hundert mal kleiner.
Bewegen sich die beiden jetzt entgegengesetzt zu einander und rauschen zusammen muss der Impuls konstant bleiben. Dh. der Mond verliert (umgekehrtes Vorzeichen bei seiner Geschwindigkeit) ungefähr ein hundertstel seines Impulses wenn er den Impuls von Ceres vollständig „aufnimmt“.
1%. Mehr nicht.
(Für die Spezialisten hier: Ich weiß, dass das eine Milchmädchenrechnung ist. Aber zur Veranschaulichung reichts, denke ich.)
@Bumms
Das ist leider falsch eingeschätzt, weil sich an der Masse ja nix ändert, nur weil Du die Reibung weg machst.
Ja, den Eindruck, den Du da hast, den kann ich schon verstehen. Ich war auch sehr erstaunt, als ich, am Steg stehend, die 14 m lange Motoryacht einfach so mit der Hand hin und her schieben konnte. Das hatte ich nicht erwartet. Aber im Wasser ist die Reibung einfach so niedrig, daß meine Kraft ausreichte.
Der Vergleich mit den Massen ist aber unfair.
Schließlich habe ich geschummelt. Die Yacht hatte fast keine Reibung mehr gegen das Wasser. Also ähnlich wie der Mond im All, der gar keine Reibung gegen den „Untergrund“ hat. Aber ich stand ja am Bootssteg mit voller Haftreibung und konnte nur deshalb mit meiner kleinen Masse was gegen die große Motoryacht ausrichten. Wenn Du ehrlich sein willst, dann musst Du bedenken, daß Dein Meteor, der den Mond schubsen soll, ja auch nicht auf einem Bootssteg steht und sich dank Haftreibung dagegen stemmen kann, sondern genauso leer im All hängt wie der Mond.
Du darft bei dem Versuch mit der Motoryacht also nicht auf dem Bootssteg stehen, sondern musst schon selber auch ins Wasser springen und dann von dort aus schwimmend (ich würden eine Schwimmweste nehmen) versuchen die Motoryacht mit Deinen 100 kg zu beeindrucken.
Was glaubst Du, was dabei raus kommt?
Ein flotter Sprung der 100kg vom Steg aufs Boot wäre eine bessere Analogie zu einem Asteroideneinschlag.
Und dessen Anschub-Wirkung kann man dann ja mal mit dem Effekt durch stetiges Drücken vergleichen – da wird schon ein Unterschied sein.
@ Kyllyeti
Jo, den flotten Sprung vom Steg auf die Motoryacht haben wir auch öfter gemacht.
@Basilios:
Jep.
Dein Beispiel mit dem Boot gefällt mir:
Man nehme einfach mal an, dass du das Boot nicht mit ein paar cm/s mit der Hand bewegt hättest, sondern dass es mit 20 km/h auf den Steg zu schwimmt und ihn zu rammen droht …
20 km/h entsprechen ungefähr 600 cm/s. Da die Geschwindigkeit in den Impuls linear eingeht, reden wir hier also von einem etwa 100fach größerem Impuls (und da der Impuls in die kinetische Energie quadratisch eingeht, von einer 10.000 fach höheren kinetischen Energie).
Du möchtest nicht am Steg stehen und das Boot mit der Hand anhalten – Reibung hin oder her :-).
@PDP10
Dein Beispiel ist total unrealistisch.
Unsere Motoryacht hatte eine maximal mögliche Höchstgeschwindigkeit von ziemlich genau 15 km/h. Deine 20 km/h………..also das geht total über meine Vorstellungskraft.
^_^
Aber ich gebe Dir Recht: Mit der Hand hätte ich das Trumm von Boot schon bei der typischerweise realistischen Reisegeschwindigkeit von 10 km/h nicht mehr anhalten wollen.
^_____^
Also wenn ich mit Schung in meinen Kanadier springe, dann treibt der anschließend ein bisschen in die Richtung weiter davon (Vorausgesetzt ich mache keinen doppelten Rittberger und lande elegant im Wasser).
Der gleiche Hoppser in die Motoryacht lässt diese vielleicht ein ganz klein wenig auf und ab Schwanken, ändert aber nix daran, daß die immer noch am Steg liegt. Der Kanadier hat aber nur rund ein Viertel unserer VergleichsMenschenNormMasse von 100 kg und die kleine Motoryacht hat dann ca. 60 Mal soviel.
Wieviel mehr Masse hatte der Mond im Vergleich zum angenommenen Impaktor?
0_0
@Basilios:
Nun, im Fall von Ceres hab ich das ja oben schon geschrieben (die Zahlen hab ich aus der Wikipedia).
Verhältnis Masse (ca.) Ceres 1 : Mond 100. Also deutlich schlechter, als Du vs. Motoryacht :-).
Und einen größeren Impaktor als Ceres muss man im Sonnensystem, glaube ich, erst mal finden.
:-).
Jepp.
OK, interessante Übrlegungen hier, danke, aber bei meiner Überlegung geht es ja gerade nicht um eine Kollision von vorne sondern von der Seite und von hinten.
Aber selbst bei einer Kollision von vorne und Deinen 1% , wenn das zu einer relevanten Bahnabweichung führen würde dann reicht das doch schon. Wenn nicht nehmen wir den Fall von der Seite oder von Hinten.
Löst Euch vom Vergleich mit den üblichen apokalyptischen Szenarien wo man dann sagt gegenüber dem ist 1 % harmlos.
Es geht nicht um 1 % oder 80 % , es geht nicht um die Auslöschung der Menschheit und auch nicht den Fall dass gar nichts passiert, sondern ich wollte über so ein Szenario nachdenken, wo sich die Mondbahn soweit ändert, dass es eine moderate Gezeitenändrung von vielleicht dem doppelten oder dreifachen gibt.
Das betrifft zuerst nur die Küste aber über den Welthandel dann doch immer mehr Menschen und man muss und kann irgendwie darauf reagieren.
„Alles-aus-Katatstrophen“ sind „langweilig“, da gibts nichts mehr zu tun,,,,
@Bumms: „sondern ich wollte über so ein Szenario nachdenken, wo sich die Mondbahn soweit ändert, dass es eine moderate Gezeitenändrung von vielleicht dem doppelten oder dreifachen gibt. Das betrifft zuerst nur die Küste aber über den Welthandel dann doch immer mehr Menschen und man muss und kann irgendwie darauf reagieren.“
Schreibst du ein Buch oder bastelst du an irgendeiner Privattheorie oder warum hast du dich da so sehr festgebissen? Die Gezeitenkraft ist ein ziemlich kompliziertes Dingens: https://scienceblogs.de/astrodicticum-simplex/?p=21340?all=1 Da spielen so enorm viele Faktoren mit rein; viel mehr als der reine Abstand zwischen Mond und Erde der sich ja – wie schon gesagt – sowieso ständig ändert. Dem Mond ist der Einschlag eines typischen Asteroiden völlig egal. Das sieht man ja auch daran, dass er ständig von typischen Asteroiden getroffen wird und wurde!
@Florian
Mich interessierts halt enfach und festgebissen hab ich weil ich mich teils nicht gut verstanden fühle aber auch danke für nützliche Infos die kamen. Das Konkreteste was sich bisher aus den Links ergeben hat ist, dass eine Halbierung des Mondabtands zu einer Verachtfachung der Gezeitenhöhe führt. Bravo und danke, das ist eine konrete Antwort.
Ausserdem ist es Allgemeinwissen dass durch Kollisionen Bahnänderungen vorkommen.
Also fragte ich wie groß so ein Körper sein müsse, damit es eine moderate aber doch wahrnehmbare Änderung der Gezeiten gibt.
Da hiess es dann zuerst „etwa gleich gross wie der Mond“
Dann jedoch lese ich in einem Artikel, dass bei „gleich gross und schnell von vorne“ der Mond natürlich ganz stehn bleibt und dann auf die Erde fällt.
Und da fühle ich mich dann nicht verstanden, weil unter dem Strich mir alles zu sehr in Extremen bleibt.
Und weil ich bei Asteroiden eben eine ca. 5-fache Mondgeschwindigkeit kenne und über m*v würde ja dann schon sowieso ein Fünftel der Masse reichen, zusätzlich dazu dass es ja dann einen Stop gäbe und es mir gar nicht um einen Stop geht
Das eine Extrem „gleich gross“ wo sich dann herausstellt dass es hier gar nicht um eine BAHNÄNDERUNG geht sondern einen Stopp und es auch dann noch fünfmal zu gross wäre. Und dann das andere Extrem wo es so wie in Deinem letzten Beitrag gar keine Auswirkung hat.
Fakt nach allen Beiträgen hier ist jetzt, dass es dankenswerte Infos gab, aber eine Abschätzung der Größenordnung für mich immer noch nicht ausreichend möglich war. Das ist kein Vorwurf, wenns hier nicht möglich ist gehts halt nicht, ich danke ja für die Geduld, will halt nur sagen um was es mir geht.
Aussagen wie „halbe Monddistanz bringt achtfache Gezeiten“ sind doch OK und in die richtige Richtung, das stand in einem Deiner Artikel und hat mir weitergeholfen, jetzt ist für mich die Frage, was kann eine solche Bahnänderung bewirken, „gleichgross“ ist es nicht, denn das bringt ja einen Stopp bzw. schon ein Fünftel davon bringt den bei entsprechender Geschwindigkeit.
Aber OK, wie gesagt, ich will nicht nerven, was hier nicht geht geht halt nicht aber wenn man viel schreibt wünscht man sich halt verstanden zu werden.
Vielleicht sollte man es auch erstmal unabhängig vom Mond sehen, kennt jemand gute anschauliche Infoquellen zum Thema Kollisionen und Bahnänderungen?
Wenn ich dann mal eine Reihe Kollisionen und Bahnänderungen studiert habe kann ich vielleicht besser abschätzen und qualifizierter dann Restfragen formulieren. Besten Dank.
@Bumms: „aber eine Abschätzung der Größenordnung für mich immer noch nicht ausreichend möglich war.“
Das ist auch nicht möglich weil die Frage sehr unkonkret gestellt ist. Wie schon gesagt: So direkt ist der Zusammenhang zwischen Mondentfernung und Gezeiten nicht. So einfach funktioniert die Himmelsmechanik auch nicht; der ABstand zwischen Mond und Erde ändert sich STÄNDIG.