„am dritten Tage auferstanden von den Toten, aufgefahren in den Himmel“, heißt es im Apostolischen Glaubensbekenntnis der römisch-katholischen Kirche. Auferstanden und aufgefahren soll natürlich Jesus Christus höchst selbst sein und stattgefunden hat die Fahrt in den Himmel 40 Tage nach Ostern; also heute (bzw. genau genommen heute, aber früher (bzw. ganz genau genommen gar nicht)), weswegen der gerade stattfindende Feiertag ja auch Christi Himmelsfahrt heißt. Wie ihr den freien Tag nutzt weiß ich nicht – hier in Thüringen spaziert man jedenfalls traditionell durch die Wälder und betrinkt sich dabei (vermutlich ganz ohne theologische Rechtfertigung). Da ich morgen aber arbeiten muss, setze ich beim Freiluftbesäufnis diesmal aus und schreibe lieber einen kurzen Text über die eigentliche Bedeutung der Ascensio, wie die Himmelfahrt in der Sprache der Kirche ja offiziell heißt.

Mich interessiert aber nicht irgendeine Aszension, sondern die „rechte“. Es geht um die Rektaszension, die allen schon mal begegnet ist, die sich mit der Beobachtung des Himmels beschäftigt haben. Wie man die Position von Objekten am Himmel angibt, habe ich früher schon recht ausführlich erklärt. Es gibt jede Menge mögliche Koordinatensysteme für die verschiedensten Anwendungen. Am häufigsten ist aber dasjenige, bei dem jedem Himmelskörper zwei Zahlen zugewiesen werden: Rektaszension und Deklination. Die spielen im wesentlichen die Rolle, die die geografische Länge und Breite auf der Erde spielen. Während Länge und Breite den Abstand zum Nullmeridian in Greenwich und zum Äquator messen, müssen wir uns bei der Rektaszension auf den Himmelsäquator konzentrieren.
Der Himmelsäquator ist der auf den Himmel projizierte Äquator der Erde. Stellen wir uns vor, wir befinden uns in der brasilianischen Stadt Macapá. Nachdem wir uns die Citadelle – offensichtlich eine von zwei lokalen Sehenswürdigkeiten – angesehen haben, können wir zur zweiten Sehenswürdigkeit spazieren: Dem Zero-Monument, das die Position des Äquators markiert, der genau durch die Stadt verläuft. Sollten wir eine Stelle mit freiem Blick auf den Horizont finden, dann würden wir feststellen, dass er den Himmelsäquator genau im rechten Winkel schneidet. Und nachdem wir das festgestellt haben, können wir die Sterne betrachten die in der – hoffentlich – klaren Nacht aufgehen und sich über den Himmel bewegen. Am Äquator tun sie das in einer geraden Linie, direkt vom Horizont nach oben über unseren Kopf hinweg und dann wieder zurück bis zum Untergang. Das ist nicht überraschend: Die Sterne bewegen sich ja nicht wirklich; es ist die Drehung der Erde um ihre Achse die die scheinbare Bewegung der Himmelskörper verursacht.
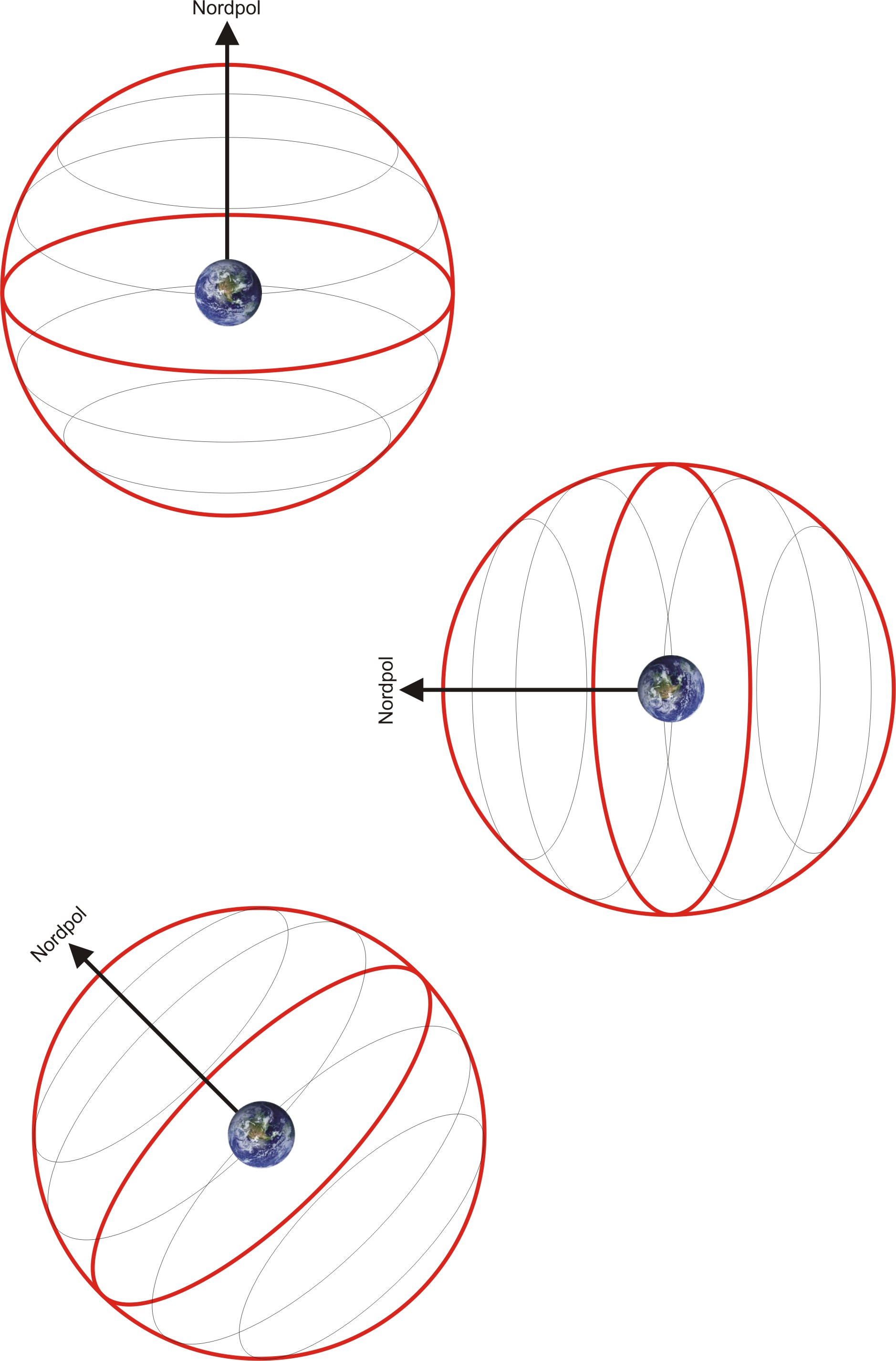
Stünden wir genau am Nord- oder Südpol, würden wir sehen können, wie sich die Sterne alle parallel zum Horizont bewegen und weder auf- noch untergehen. Zum Glück sind wir aber im warmen Brasilien und sehen hier am Äquator jeden Stern auf- und untergehen und zwar in rechtem Winkel zum Horizont. Der Aufstieg der Gestirne erfolgt also gerade. Oder wie man früher gesagt hat: Es handelt sich um eine ascension recta. Eben die Rektaszension.
In der modernen Astronomie bezeichnet die Rektaszension einen Winkel der vom Frühlingspunkt aus entlang des Himmelsäquators bis zum Fusspunkt unter dem Sterns gemessen wird. Der Frühlingspunkt ist der Nullpunkt des Koordinatensystems; es handelt sich um den Schnittpunkt zwischen Himmelsäquator und der Ekliptik, also der scheinbaren Bahn der Sonne um die Erde (die der realen Bahn der Erde um die Sonne entspricht). Vereinfacht gesagt: Wenn man einen Stern betrachtet, dann ist des Höhe über dem Himmelsäquator seine Deklination. Zieht man vom Stern einen Kreisbogen nach unten der im rechten Winkel auf dem Himmelsäquator trifft und misst den Abstand von diesem Punkt zum Frühlingspunkt, erhält man die Rektaszension.
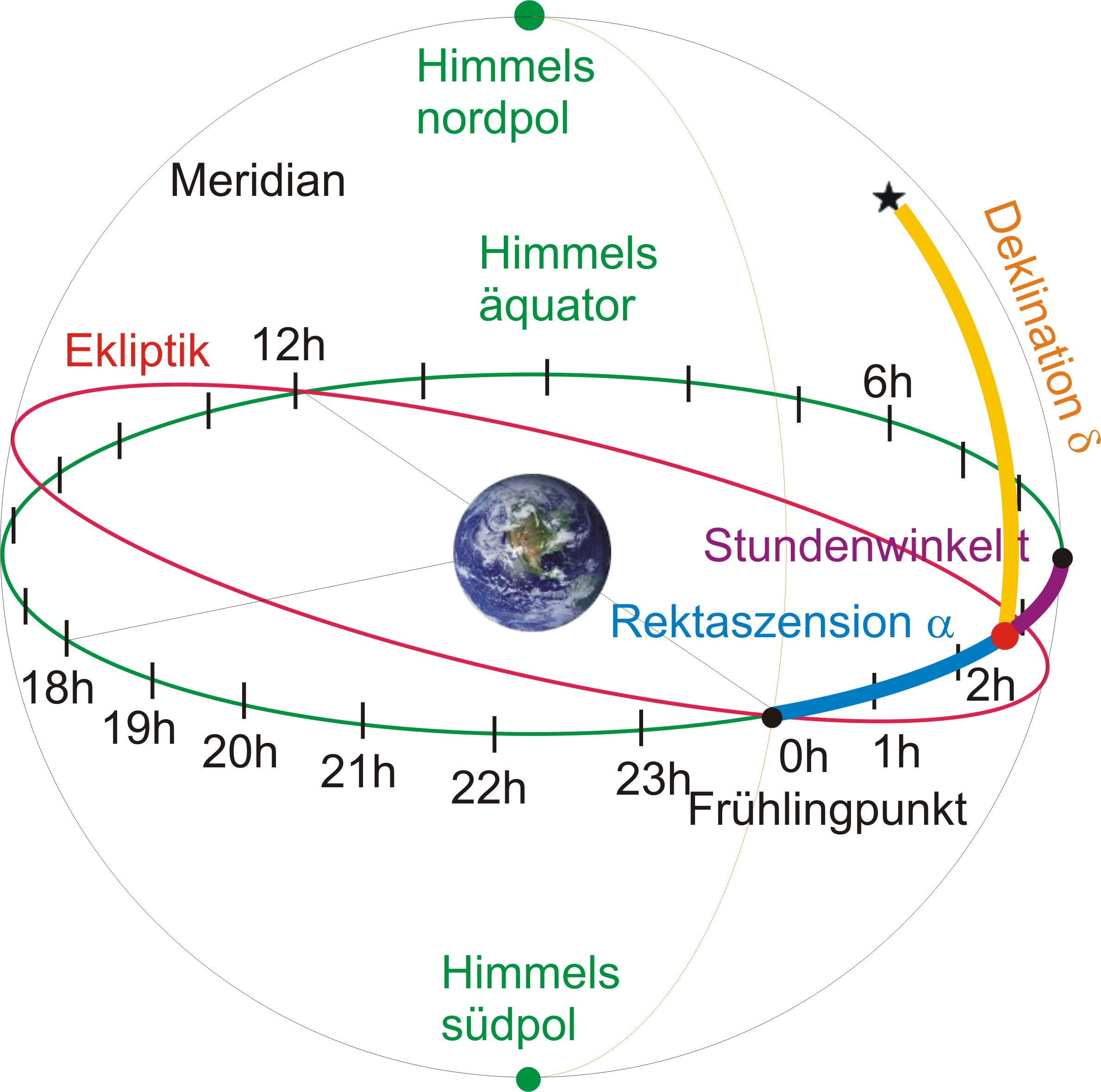
Alles ganz einfach, oder? Auf jeden Fall viel einfacher als die christliche Theologie mit den lebenden Toten die zwischen Himmel und Erde herum sausen ohne vorab vernünftige Koordinatensystem zu entwickeln!
Wie kommt es nur, dass ich beim Lesen des Artikeltitels nicht an religiöse Verzällscher, sondern an dieses Video denken musste?
Das stimmt in dieser Präzision nicht. Je nachdem, welche Stelle im NT bezüglich der „Himmelfahrt“ aufschlägt, war es entweder am Tag der „Auferstehung“, vier Tage, viele Tage oder aber 40 Tage danach, wobei man letztere wohl hauptsächlich deshalb für das entsprechende Fest gewählt hat, um einen gewissen zeitlichen Abstand zu Ostern zu bekommen.
Wie man sieht, widerspricht sich die Bibel also auch in diesem Punkt.
@Jonas: „Das stimmt in dieser Präzision nicht.“
Christi Himmelfahrt wird 40 Tage nach Ostern gefeiert. Darum ist es ja auch immer ein Donnerstag. Dass Jesus in der Realität nicht in den Himmel aufgefahren ist, muss nicht extra betont werden. Ich habe halt nur erwähnt, WAS das heute für ein Feiertag ist und warum er heute gefeiert wird. Die Kirche hat sich auf diesen Tag festgelegt.
Was ich mich schon immer gefragt habe: Wie kommt man von den scheinbaren Bahnen am Himmel auf die realen Bahnen im All?
Vielleicht könntest du ja darüber mal eine Serie schreiben.
@BerndB: Die Frage versteh ich nicht. Was genau meinst du? Sterne? Planeten? Ich hab mich jetzt hier ja nur mal auf die Sterne bezogen; deren Bewegung in erster Näherung ja nur durch die Rotation der Erde entsteht. Ansonsten ist es halt einfach ne Koordinatentransformation. Je nachdem worauf sich deine Koordinatensystem bezieht und wo der Nullpunkt ist, beschreibst du verschiedene Bewegungen. Aus Sicht der Erde; aus Sicht der Sonne; aus Sicht des galaktischen Zentrums, usw.
@Florian
<nitpick>Das tun streng genommen nur diejenigen Sterne, die genau im Osten aufgehen. Sterne nördlich und südlich davon ziehen dazu parallele Bögen, die nicht durch den Zenit gehen. Der durch die Refraktion angehobene Polarstern zieht einen kleinen Dreiviertelkreis am Nordhorizont.</nitpick>
I know, die Tyrannei der Präzision, aber dafür sind ja die Kommentare gut… 😉
Meine Frage war eher allgemeiner Natur und ich nahm nur den Artikel zum Anlass.
Wir können ja auf der Erde erstmal nur in unserem erdgebundenen Bezugssystem aus beobachten und Winkel-Koordinaten angeben.
Aber wie werden daraus dann die Bahnen im Sonnensystem (Bezugssystem Sonne als Mittelpunkt) für Kometen und Asteroiden berechnet. Für die haben wir ja meistens erstmal keine Entfernung.
Bei Sternen bzw. Galaxien stelle ich mir das einfacher vor. Da kann man ja inzwischen die ungefähren Entfernungen mit verschiedenen Methoden berechnen/messen und kann dies so mit den Winkelkoordinaten in ein 3D-Modell übertragen.
Netter Aufhänger für einen Artikel über die Benennung von perspektivischen Effekten auf den Eindruck vom (Nacht)-Himmel.
Aber es ist eigentlich viel einfacher.
„Und es geschah, als er sie segnete, schied er von ihnen und fuhr auf gen Himmel.“ (Lk 24,51)
„Und als er das gesagt hatte, wurde er zusehends aufgehoben, und eine Wolke nahm ihn auf vor ihren Augen weg. Und als sie ihm nachsahen, wie er gen Himmel fuhr, siehe, da standen bei ihnen zwei Männer in weißen Gewändern.“ (Apg 1,9 f.)
„Nachdem der Herr Jesus mit ihnen geredet hatte, wurde er aufgehoben gen Himmel und setzte sich zur Rechten Gottes.“ (Mk 16,19)
Eine Richtung ist nirgends angegeben. Nur immer „gen Himmel“, also im Zweifel senkrecht nach oben. (Wenn er irgendwie schief, schräg oder in einem kühnen Bogen aufgefahren wäre, hätten die Chronisten das bestimmt überliefert.)
Und das tat er natürlich von Jerusalem aus. Jetzt muss man also nur noch feststellen, wo genau sich die Erde zum Zeitpunkt der Auferstehung im Bezug auf ein geeignetes Koordinatensystem befand, und dann natürlich noch berücksichtigen, dass die genaue Uhrzeit wichtig ist. Weil sich Jerusalem ja jeden Tag einmal rundrumdreht. Und dann geht man einfach von da aus senkrecht nach oben. Und da ist dann der Himmel.
@BerndB: da niemand mit Kompetenz bisher antwortet, versuche ich es mal als Laie.
Es ist eher anders herum: in unserem Sonnensystem können wir Entfernungen echt gut messen, nennt sich Parallaxen-Methode:
https://de.wikipedia.org/wiki/Parallaxe
Damit hast Du die dritte Koordinate für 3D.
Bei den Abständen zu den Sternen standen die Astronomen lange Zeit auf dem Schlauch, bis Henrietta Leavitt eine neue Methode gefunden hat. Die Parallaxen-Methode funktionierte (bis zur Einführung von Weltraumtelesopen) nur für die nächsten Nachbarsterne, und die muss man erst mal finden.
@BerndB: So ganz versteh ich die Frage immer noch nicht. Nur weil wir auf der bewegten Erde sind, folgt daraus ja nicht das es irgendwie per se problematisch ist, festzustellen wie sich anderes Zeug anderswo bewegt. Das sind einfach Transformationen zwischen verschiedenen (bewegten) Koordinatensystemen. Du kannst aus Rektaszension/Deklination die heliozentrischen Bahnelemente von Himmelskörpern berechnen. Oder die galaktischen Koordinaten. Oder umgekehrt. Und so weiter. Natürlich ist die Mathematik nicht trivial – aber jetzt auch nicht dramatisch schwer. Siehe zB hier: https://www.stjarnhimlen.se/comp/tutorial.html
Als ich ganz klein war, gab es wohl mal am Himmelfahrtstag einen Raketenstart im Fernsehen (könnte ein Apollo gewesen sein). Seitdem dachte ich, dass Himmelfahrt der Tag ist, an dem die Menschen immer zum Mond fliegen.
@Stefan, schöner Text :))
Ja, die Koordinatentransformation meinte ich. Für dich ist das vielleicht logisch, aber für Otto-Normalbürger nun nicht unbedingt. Wenn ich, sagen wir mal, einen neuen Asteroiden finde, dann habe ich ja erstmal nur wenige Datenpunkte am Himmel. Diese möchte ich nun zu einer Bahn vervollständigen.Wieviele Datenpunkte braucht es da und wie kommt man halt von der scheinbar geraden Bahn am Himmel auf die elliptischen Bahndaten, damit es dann so schöne Diagramme gibt, wie die Teile sich um die Sonne bewegen.
@BerndB
Man braucht 3 Positionen, die möglichst weit auseinander liegen, um eine Bahnellipse zu bestimmen. Die Entfernung ist dabei nicht einmal nötig (Kepler hat z.B. die Bahn des Mars relativ zur Astronomischen Einheit bestimmen können, lange bevor man eine Idee hatte, wie groß diese ist). Natürlich muss man wissen, wo genau sich jeweils die Erde befindet. In den drei Richtungen zum Objekt steckt implizit schon dessen Bewegungsgeschwindigkeit und damit die Entfernung drin. So ein Objekt kann ja nicht jede beliebige Bahn vollführen, sondern es muss eine Keplerellipse sein, das schränkt die möglichen Lösungen ein, so dass drei Richtungen ohne Entfernung ausreichen, um die Bahn zu bestimmen. Wenn man mehr Positionen hat, kann man die Bahn genauer bestimmen, aber am wichtigsten ist, wie gesagt, dass wenigstens eine der Positionen hinreichend weit von den anderen entfernt liegt, denn durch drei nahe beieinander liegende Positionen mit Messfehlern kann man viele Bahnen ziehen, die am Ende stark voneinander abweichen.
Viel Glück beim Berechnen der Himmelfahrtskommando-Routen!
Hier https://neo.jpl.nasa.gov/risk/a99942.html
steht „99942 Apophis (2004 MN4)
Analysis based on 13 radar delay, 7 Doppler, and
4147 optical observations spanning 3635.5 days“.
Wurde also 13 mal nur die Laufzeit und nicht auch noch die Phasenverschiebung gemessen?
@Mac-FD
Was willst Du denn mit der Phasenverschiebung messen, die Wellenlänge des Radars ist doch sehr klein gegen das Objekt, und man möchte nur dessen Position (Entfernung, Richtung) möglichst genau bestimmen Außerdem wurde der Doppler, also die Bewegung auf uns zu bzw. von uns weg, gemessen, sowie der optische Ort (geht, glaube ich, noch genauer als Radar, welches wiederum die Entfernung viel genauer messen kann).
Noch wichtiger ist, die Messungen in hinreichendem zeitlichem Abstand zu machen, damit man mehrere Orte entlang der Bahn des Asteroiden bestimmt hat. Und das steckt in den 3635,5 Tagen drin, das sind ja fast 10 Jahre und somit mehrere Umläufe um die Sonne. Die Bahn von Apophis ist also sehr genau bekannt.
Das man seit fast 10 Jahren die Bahn vermisst musste ich auch noch nicht. Das war mehr als Info für BerndB gemeint. VK184 brauchte min. 2 Jahre bis er bei NEO mit 0 in der Torino-Scale war (Siehe https://neo.jpl.nasa.gov/torino_scale.html).
Das mit der Wellenlänge vom Radar habe ich nicht Bedacht.
Aber WO ist denn nun der Unterschied zwischen den 13 Radar und den 7 Doppler Beobachtungen?
Ich wüsste gerne mit welchen „Instrumenten“ die Radar-Messungen gemacht werden und wo die Unterschiede sind.
Möchte Wetten es gibt hier schon was dazu.
@Mac-FD: Das macht man mit Radioteleskopen. Siehe hier: https://scienceblogs.de/astrodicticum-simplex/2014/06/05/mit-dem-fahrrad-zu-den-asteroiden-abschnitt-9-bei-den-radioteleskopen-in-der-wachau/?all=1
Vielen Dank für die Info
Die 7 Doppler waren also dazu da die Form zu Bestimmen.; also ein „Foto“ zu machen!(?)
Man muss aber dazu doch wohl die „Instrumente“
(Siehe https://scienceblogs.de/astrodicticum-simplex/files/2014/05/ADU-1000-3-500×666.jpg ) zu einem VLB-Array vereinigen!(?)
Deswegen also nur 7 „Doppler“ (Laut Wiki ist der Begriff Doppler eh falsch)
@Mac-FD
Man muss für so eine Abbildung kein Array zusammenschalten, sondern nur Laufzeit und Doppler messen. Die sogenannten „Radar-Bilder“ der Asteroiden plotten in der Horizontalen den Doppler aufgrund der Drehung des Objekts – die eine Seite ist zu längeren Frequenzen verschoben, weil sie sich von uns wegdreht, die andere zu kürzeren, weil sie auf uns zu kommt. Dabei spielt die räumlich Orientierung keine Rolle, das Diagramm ändert sein Aussehen nicht, wenn Du den Asteroiden in Gedanken um eine Achse entlang der Sichtlinie zur Erde rotieren lässt. Allerdings wirkt sich die Orientierung der Achse des Asteroiden aus: zeigt die nämlich genau auf uns zu, dann würde er schmäler erscheinen, als wenn man auf den Äquator guckt. Da nicht alle Asteroiden gleich schnell rotieren, müsste es da auch schmalere und breitere geben, aber vermutlich normiert man alles auf die Breite des Diagramms.
In der Senkrechten wird die Laufzeit aufgetragen. Punkte des Asteroiden, die näher sind, erscheinen an einem Ende der Achse, fernere am anderen. Das heißt, das gleich weit entfernte Punkte nördlich und südlich der Mittellinie (mit gleichem Doppler) an der selben Stelle im Diagramm landen.
Was man erhält, sieht zwar wie ein Bild des Asteroiden aus, aber es ist keines. In der Realität sähe das Objekt vermutlich völlig anders aus. Man kann aber durchaus die Größe des Objekts auf diese Weise abschätzen.
Dass die Zahl der Doppler-Messungen kleiner ist als die der Radar-Messungen überhaupt könnte daran liegen, dass nicht alle Radarmessungen mit einem Gerät erfolgten, dass den Doppler hinreichend genau (oder überhaupt) bestimmen kann. Dann wären die Doppler-Messungen eine Teilmenge der Radarmessungen überhaupt. Soviel ich weiß machen nur Arecibo und Goldstone abbildende Dopplermessungen.