Heute ist der 14. März. Schreibt man das auf die (zugegebenermaßen umständliche) amerikanische Weise, dann lautet das Datum heute 3/14. So beginnt auch die Kreiszahl Pi und deswegen wird an diesem Tag der Internationale Pi-Tag gefeiert. Ein Ereignis, das ich als offizieller Pi-Botschafter nicht einfach vorüber gehen lassen kann.
Es mag ein wenig seltsam anmuten, einer Zahl einen Feiertag zu widmen oder gar „Botschafter“ einer Zahl zu sein. Aber noch seltsamer wäre es, sich nicht mit Pi zu beschäftigen. Ich kann mich ihrer Faszination jedenfalls nicht entziehen.

Die Zahl Pi könnte kaum einfacher definiert sein. Ein Kreis hat einen Umfang und einen Durchmesser. Teilt man das eine durch das andere, erhält man eine Zahl, die für jeden Kreis identisch ist: Pi. Und trotz dieser absoluten Einfachheit und der für jeden verständlichen Definition taucht diese Zahl überall auf. Und wenn ich „überall“ sage, dann meine ich auch überall.
Nicht nur bei der Berechnung von Eigenschaften eines Kreises. Die Zahl findet man genau so in den Formeln die die Entstehung des Universums beschreiben oder den Aufbau der Materie. Man findet sie in den fundamentalen Gleichungen der Relativitätstheorie und der Quantenmechanik. Die Ausbreitung des Lichts, die Bewegung von Himmelskörpern; bis hin zur Technik des Alltags: All das lässt sich nur mit Kenntnis der Kreizahl Pi verstehen.
Ein Beispiel: Das heute Pi-Tag gefeiert wird, ist ja eine recht willkürliche Angelegenheit. Würden wir ein anderes Zahlensystem oder einen anderen Kalender verwenden, dann gäbe es eine andere Übereinstimmung zwischen Zahl und Datum. Aber so wie es nun mal ist, ist der 14.3. der Tag, an dem Pi gefeiert wird. Und an diesem Tag ist natürlich auch jede Menge anderes passiert. Albert Einstein wurde geboren (und über den Zusammenhang zwischen seiner Arbeit und Pi habe ich früher schon geschrieben). Karl Marx ist gestorben. Und im Jahr 1784 hat der Astronom Wilhelm Herschel an diesem Tag die NGC 4394 entdeckt.

Es handelt sich dabei um eine sogenannte Balkenspiralgalaxie, der gleiche Typ zu dem auch unsere Milchstraße gehört. Eine Balkenspiralgalaxie hat nicht nur Spiralarme, die aus einem Zentrum – dem Bulge hervorgehen, sondern zusätzlich eine balkenartige Struktur, die dazwischen sitzt und den Bulge mit den Spiralarmen verbindet. Wieso Galaxien solche Balken entwickeln; ob sie das früh in ihrer Existenz tun und ihn später wieder verlieren oder umgekehrt und wie sich der Balken genau ausbildet: Das alles sind Fragen, auf die die Astronomen noch keine abschließende Antwort gefunden haben.
Deswegen ist die Untersuchung der Morphologie von Galaxien ein immer noch sehr aktives Forschungsgebiet. Und da NGC 4394 einen wirklich schönen und ausgeprägten Balken besitzt, dient sie oft als Ausgangspunkt für solche Arbeiten. Wie zum Beispiel im Artikel „A Technique for Separating the Gravitational Torques of Bars and Spirals in Disk Galaxies“ den Ron Buta von der Universität Alabama und seine Kollegen im Jahr 2003 veröffentlicht haben.
Die Arbeit ist ziemlich technisch und gehört zu den eher wenig spektakulären Beispielen astronomischer Forschung. Was nicht heißt, dass sie nicht wichtig ist! Buta und seine Kollegen haben sich überlegt, mit welchen Methoden man bei Aufnahmen von Galaxien am besten den Anteil des Lichts der vom Balken stammt vom Licht der restlichen Galaxie trennen kann. Wenn man das nicht kann, ist es auch schwer, den Balken im Detail zu erforschen und Antworten auf all die offenen Fragen zu finden, die ich oben aufgelistet habe.
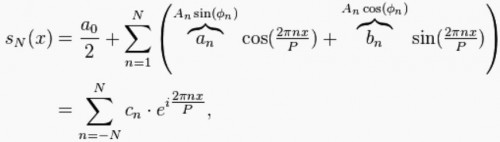
Ich will die Methode gar nicht im Detail erklären; es reicht für heute zu wissen, dass sie auf der Technik der Fourierreihen basiert. Damit ist es möglich, eine (komplizierte) mathematische Funktion als Summe von (weniger komplizierten) anderen Funktionen darzustellen. Fourierreihen findet man auch so gut wie überall in den Naturwissenschaften – und selbstverständlich benötigt man zur Berechnung dieser komplexen Summen auch die Kreiszahl Pi!
Wenn wir also wissen wollen, wie Galaxien funktionieren, dann geht das nur, wenn wir dabei auch die Zahl benutzen, die das Verhältnis von Umfang zu Durchmesser eines simplen Kreises beschreibt. Und was für die Galaxien gilt, gilt auch für den Rest des Universums. Ohne Kreiszahl gibt es keine Erkenntnis.
Deswegen: Nutzt diesen Tag, um ein wenig über die erstaunlich simple, erstaunlich komplizierte und erstaunlich wichtige Kreizahl Pi nachzudenken. Ich wünsche einen frohen Pi-Tag!
Na dann alles Gute zum Pi-Tag! 🙂
Mich hat vor einiger Zeit vor allem der Zusammenhang zwischen Pi und den Primzahlen fasziniert (Pi²/6). Aber ebenso auch der Zusammenhang zu den Quadratzahlen und selbst zu den ungeraden Zahlen (Pi/4 = 1/1 – 1/3 + 1/5 – 1/7 + 1/9 – 1/11 …).
Der Grund dafür ist ja noch unbekannt. Aber er zermürbt mir auf jeden Fall kräftig den Kopf, wenn ich darüber nachdenke.
Florian, hast Du heute schon fleißig die ersten hundert Stellen von Pi vorgetragen ? 🙂
@Grant:
Naja, Eulers Lösung des Basler Problems zeigt doch ziemlich offensichtlich, warum die Summe der reziproken Quadratzahlen gleich π²/6 ist (obwohl sie natürlich formal nicht ganz sauber ist). Unbekannt ist der Grund also nun wirklich nicht. Zumal: Was heißt „Der Grund dafür ist ja noch unbekannt.“ wenn doch Beweise für diese Formeln vorliegen?
@Grant:
Über eine philosophische Sichtweise, (oder sogar was für Querdenker?)
ist hier recht Ungewöhnliches über Pi zu bestaunen. 🙂
P.S.: Der Rest ist auch nicht ganz ohne Reiz. 😉
Ich sag mal so. Nachdem es in der Physik oft drum geht, dass Kräfte zwei Massen in Kreisbahnen zwingen und/oder es zu harmonischen Schwingungen kommt, muss die Zahl PI geradezu überall drin vorkommen. Trotzdem faszinierend wie das alles zusammenhängt, so wie die Formel in der fast alle mathematischen Konstanten vereint sind:
e^^(i * PI) -1 = 0
ich wage mal eine andere Annäherung an das Thema
Warum können Seeräuber keine Kreisberechnungen?
weil sie Pi raten.
oh… den kanntet ihr schon?
Das ist so wie:
Warum gehen Fliegen nicht in die Kirche:
Sie sind Insekten.
Aber Vorsicht: So bloß nicht zu Pi-phemisch hier 🙂
@Hugo
sorry, ich bezog mich eigentlich auf die Primzahlen, war nicht ganz deutlich.
@Vortex
danke für den Link. Schöne Seite, ist gleich gebookmarkt.
@Grant:
Welchen Zusammenhang zwischen Pi und den Primzahlen meinst du genau? Mir würde eine Reihe von Formeln einfallen die (mehr oder weniger direkt) beides beinhalten. Aber was der Zusammenhang sein soll, ist mir nicht klar.
Selbstverständlich wurde heute Kuchen mit auf Arbeit genommen – allerdings ein herzhafter, bzw zwei, Striezel, einmal mit Frischkäse+Paprika-, der andere mit Hackfleisch+Sauce-Füllung. Yummy!
moin hugo, ich kann zwar nicht garantieren, daß ich Grants Assoziation richtig errate (but I can grant not to be Grant), doch die Angaben führen mich zu Rieman, seiner Vermutung, seiner Zeta-Funktion und da insbesondere zu Zeta(2).
Ich hätte ja sehr gerne dieses Bier hier: https://www.tapitbrewing.com/beer/pi-golden-ale/?age-verified=d2d66fa7b7
Aber das scheint in Deutschland/Österreich kaum irgendwie erhältlich zu sein…
@rolak:
Hm. Aber ζ(2) ist doch gerade das Basel-Problem, und das meint Grant ja anscheinend nicht.
ich meinte diesen Zusammenhang:
(2²/(2²-1)) * (3²/(3²-1)) * (5²/(5²-1)) * (7²/(7²-1)) * … = π²/6
Ach Fourier-Reihen sind extrem wichtig in unserer Zeit. Man kann sie zum Beispiel dazu verwenden um in einem Bild die „wichtigen“ von den „unwichtigen“ Informationen zu trennen, was die Grundlage von JPEG ist. Dank des Algorithmuses den man „Schnelle Fourier Transformation“ nennt, kann man bestimmte Sachen sehr viel schneller berechnen als sonst. GSM Mobiltelefone nutzen das zum Beispiel um den genauen Zeitpunkt des gesendeten Signales zu bestimmen um zu wissen, welches Bit denn wo im Burst ist, usw.
@Grant:
Aber das ist doch nur die Darstellung von ζ(2) als Euler-Produkt. D.h. wenn man auf Rigorosität nicht so viel Wert legt, braucht man nur den Hauptsatz der elementaren Zahlentheorie (Eineindeutigkeit der Primfaktorzerlegung) um auf die Summe der Inversen der Quadratzahlen so kommen.
@rolak / #9:
Aus dem Archiv hier eine aktuelle Ausgabe (August 31, 2015)
proof-riemann.pdf … falls noch von Interesse?
P.S.: Da ich neugierig war, versteh darin aber fast gar nichts.
Ich wünsche die Aufnahme von in den Glaubenskanon seiner Nudeligkeit. Immerhin sind Hackbällchen rund.
„von Pi“
Liest hier eigentlich noch jemand zur Korrektur mit?
@Franz #4:
Die Eulersche Identität lautet exp( i * Pi ) + 1 == 0 oder exp( i * Pi ) == (–1 + 0*i) .
Es dürfte aber auch gelten:
exp( i * 2Pi ) == (1 + 0*i) und exp( i * Pi/2 ) == (0 + 1*i) .
Western Digital hat zu Ehren des Pi-Day etwas ganz besonderes präsentiert. 🙂
Dann kommt auch noch der 22/7 Day