So gut wie alle Energie die wir nutzen kommt von der Sonne. Aber wie kriegt die Sonne das eigentlich hin? Was stellt sie an, um diese großen Mengen an Energie zu produzieren? Klar, dort findet Kernfusion statt. Wasserstoff wird zu Helium. Aber wenn man die Sache genau betrachtet, ist es schon ein klein wenig komplizierter. Wie unser Stern aus Materie Energie macht und damit unsere Lebensgrundlage sichert, ist das Thema der aktuellen Folge der Sternengeschichten.
(Und weiter unten gibt es wie immer eine Transkription des Podcasts zum Nachlesen)
Die Folge könnt ihr euch hier direkt als YouTube-Video ansehen oder direkt runterladen.
Den Podcast könnt ihr unter
abonnieren beziehungsweise auch bei Bitlove via Torrent beziehen.
Am einfachsten ist es, wenn ihr euch die „Sternengeschichten-App“ fürs Handy runterladet und den Podcast damit anhört.
Die Sternengeschichten gibts natürlich auch bei iTunes (wo ich mich immer über Rezensionen und Bewertungen freue) und alle Infos und Links zu den vergangenen Folgen findet ihr unter https://www.sternengeschichten.org.
Und natürlich gibt es die Sternengeschichten auch bei Facebook und bei Twitter.
Transkription
Sternengeschichten Folge 168: Die Energie im Inneren der Sonne – Teil I
So gut wie die gesamte Energie die wir auf der Erde verwenden, stammt von der Sonne. Bei Solarenergie ist der Zusammenhang direkt erkennbar. Aber auch beim Rest steckt am Ende die Sonne dahinter. Wind entsteht durch die Temperaturunterschiede in der Erdatmosphäre die von der Sonne verursacht werden. Der Wasserkreislauf wird durch die Sonne angetrieben. Fossile Brennstoffe enthalten die Sonnenenergie, die vor Jahrmilliarden dort gespeichert wurde. Selbst die Kalorien in unserer Nahrung sind ultimativ auf die Sonne zurück zu führen: Pflanzen nutzen ihr Licht direkt für die Photosynthese und wandeln es in chemische Energie um und wenn wir Fleisch essen, dann haben diese Tiere ihre eigene Energie zuvor ebenfalls aus Pflanzen oder anderen Tieren die Pflanzen essen gewonnen. Mit der Ausnahme von Kernenergie stammt alles von der Sonne (und die radioaktiven Elemente wurden immerhin in anderen Sternen produziert).
Aber wie genau schafft es die Sonne, die großen Mengen an Energie bereit zu stellen? Klar, dort wird Wasserstoff zu Helium fusioniert. Aber wie läuft das im Detail ab? Und wie gelangt das, was im Inneren unseres Sterns erzeugt wird dann am Ende zur Erde?

Die Entstehung eines Sterns ist ein ziemlich kniffliges Thema, und eines, über das man ziemlich viel erzählen muss, um es komplett zu verstehen. Ein wenig davon habe ich schon in den Folgen 1 und 110 der Sternengeschichten erzählt. Für diese Folge reicht es, wenn wir die ganzen Frühphasen der Sternentstehung überspringen und gleich zu einem fertigen Stern wie unserer Sonne springen.
Damit ein Stern überhaupt Wasserstoff zu Helium fusionieren kann, muss die Temperatur hoch genug sein. Je höher die Temperatur, desto schneller bewegen sich die Atome und je schneller sie sich bewegen, desto größer ist die Wucht, mit der sie bei Kollisionen aufeinander prallen. Und nur wenn die groß genug ist, kann die Abstoßungskraft überwunden werden, die zwischen ihnen wirkt.
Denn die Wasserstoffatome sind ja elektrisch geladen und stoßen einander ab, wenn sie zu nahe kommen. Beziehungsweise die Kerne der Wasserstoffatome sind es und um die geht es bei der Fusion auch. Die Temperaturen im Inneren von Sternen sind im Allgemeinen immer so hoch, dass die negativ geladenen Elektronen der Atomhülle sich lösen und nur noch der elektrisch positiv geladene Kern übrig bleibt. Und wenn da die Temperatur noch höher als ungefähr 3 Millionen Grad ist, können die Atomkerne verschmelzen, wenn sie aufeinander treffen.
Im Kern der Sonne liegt die Temperatur bei ungefähr 15 Millionen Grad; das reicht also für die Kernfusion. Neben der Temperatur muss es aber auch noch genug Teilchen geben, damit am Ende ausreichend Energie erzeugt wird. Aber im Inneren von Sternen ist auch die Dichte enorm groß. In der Sonne liegt der Druck bei 200 Milliarden Bar, ist also 200 Milliarden mal größer als der normale atmosphärische Druck auf der Erdoberfläche.
Es gibt also sehr viele Teilchen auf sehr wenig Raum die sich sehr schnell bewegen. Sie können kollidieren, verschmelzen und dabei Energie freisetzen. Aber das ist natürlich noch längst nicht alles! Wasserstoff kann auf verschiedene Art und Weise zu Helium werden. Ein wichtiger Weg ist die sogenannte „Proton-Proton-Reaktion“.
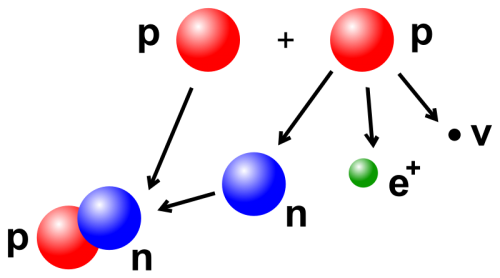
Sie beginnt, wenn zwei Wasserstoffkerne zu Kern eines Deuteriumatoms verschmelzen. Deuterium ist noch kein Helium sondern ein Isotop des Wasserstoffs. Ein normales Wasserstoffatom hat im Kern ja nur ein einziges Proton; ein Wasserstoffkern ist nichts anderes als ein Proton. Treffen zwei davon aufeinander, kann eines in ein Neutron umgewandelt werden und man bekommt einen neuen Kern der aus einem Proton und einem Neutron besteht. Dieses Element nennt man Deuterium und zusätzlich wird bei der Reaktion noch ein Positron und ein Neutrino frei. Das Neutrino saust sofort davon, da diese Teilchen ja so gut wie nie mit anderer Materie reagieren. Das Positron ist das Antiteilchen des Elektrons und von denen gibt es im Kern der Sonne ebenfalls jede Menge (all die Elektronen zum Beispiel, die früher mal Teil der Atomhüllen der Wasserstoffatome waren). Das Positron trifft also ziemlich schnell auf ein Elektron, beide vernichten sich gegenseitig und es wird Energie in Form von Gammastrahlung frei.
Die Sache geht aber noch weiter: Der Deuteriumkern kann nun mit einem weiteren Wasserstoffkern reagieren. Nun entsteht ein Atom mit zwei Protonen und einem Neutron im Kern; also sogenanntes „Helium-3“. Typischerweise reagieren im nächsten Schritt nun zwei Helium-3-Kerne um am Ende endlich das stabile und normale Helium-Atom mit zwei Protonen und zwei Neutronen zu erzeugen. Zusätzlich werden hier auch noch zwei Wasserstoffkerne frei, die für neue Reaktionen zur Verfügung stehen.
In ungefähr neun Prozent aller Fälle kann in der Sonne aber auch noch ein anderer Weg eingeschlagen werden. Die Sonne gehört ja zur dritten Generation der Sterne, enthält also neben dem beim Urknall erzeugten Elementen Wasserstoff und Helium auch schon andere, schwerere chemische Elemente die zuvor in anderen Sternen erzeugt worden sind. Die können nun ebenfalls für Kernreaktionen verwendet werden. Aus Helium-3 und normalen Helium kann zum Beispiel Beryllium entstehen, das zu Lithium zerfällt und das wiederum kann mit Wasserstoff zu Helium fusionieren. Ein weiterer Weg führt über die Verwendung von Beryllium und Bor. Welche Reaktion mit welcher Häufigkeit stattfindet, hängt von der Temperatur ab. Damit die Kernreaktionen mit Beryllium, Bor oder Lithium wirklich effektiv laufen braucht es aber Temperaturen, die höher sind, als sie derzeit im Inneren der Sonne herrschen; diese Prozesse werden also erst später so richtig relevant, wenn unser Stern ein wenig heißer geworden ist. Und in Sternen, die noch viel größer sind als unsere Sonne gibt es wieder ganz andere Prozesse.
Zum Beispiel den sogenannten Bethe-Weizsäcker-Zyklus. Damit dieser Prozess funktioniert muss ein Stern nicht nur Wasserstoff und Helium besitzen, sondern auch schon geringe Mengen an Kohlenstoff. Dann kann eine komplexe Kette von Reaktionen aus Wasserstoff Helium machen. Alles beginngt mit Kohlenstoff und Wasserstoff, die zu Stickstoff verschmelzen. Dieses Stickstoff-Atom ist allerdings instabil und zerfällt zu einem Isotop des Kohlenstoffs, das nun mit einem weiteren Wasserstoff zu stabilen Stickstoff verschmelzen kann. Der fusioniert mit Wasserstoff, erzeugt ein instabiles Sauerstoffatom, das zu einem anderen Isotop stabilen Stickstoffs verschmilzt. Das kann nun ein weiteres Mal mit Wasserstoff fusionieren und erzeugt jetzt endlich Helium und ein neues Kohlenstoffatom; genau von der Art das auch schon ganz zu Beginn beteiligt war. Am Ende ist also über einen großen Umweg aus Wasserstoff Helium geworden und der Kohlenstoff ist nicht verbraucht worden sondern wurde nur als Katalysator verwendet.
Welcher Prozess für die Energieproduktion der Sonne verantwortlich war wusste man übrigens lange nicht. Man kann ja nicht in den Kern hinein schauen und nachsehen, welche Atome da herum sausen und verschmelzen. Bethe-Weizsächer-Zyklus und Proton-Proton-Reaktion unterscheiden sich aber in der Art und der Menge der Neutrinos, die dabei frei werden. Diese Teilchen zu detektieren ist aber enorm knifflig, wie ich in Folge 103 der Sternengeschichten ja beschrieben habe. Es hat bis in die 1960er Jahren gedauert, bis man Neutrinos aus dem Inneren der Sonne nachweisen und feststellen konnte, dass die Energieproduktion dort über die Proton-Proton-Reaktion stattfindet.
Mittlerweile weiß man auch, dass der Bethe-Weizsäcker-Zyklus erst ab Temperaturen von mehr als 14 Millionen Grad funktioniert und erst ab 30 Millionen Grad so richtig effektiv wird. Er spielt also vor allem in großen Sternen eine wichtige Rolle, aber nicht bei so kleinen und vergleichsweise kühlen wie unserer Sonne.
Genaugenommen wäre es aber in der Sonne nicht einmal heiß genug, um die normale Proton-Proton-Reaktion ablaufen zu lassen. Im allerersten Schritt müssen da ja zwei Wasserstoffkerne zu einem Deuteriumkern verschmelzen. Bei den Temperaturen im Kern der Sonne kommt das aber nur sehr selten vor. So selten, dass es eigentlich nicht reichen würde, um die Menge an Energie zu erklären, die sie produziert. Die Abstoßungskraft ist zu stark und die durchschnittliche Geschwindigkeit der Wasserstoffkerne zu gering. Warum es trotzdem funktioniert hat man erst verstanden, als die Quantenmechanik entwickelt wurde. Der sogenannte „Tunneleffekt“ sorgt bei Teilchen dafür, dass sie einander auch nahe kommen können, obwohl die Abstoßungskraft zu groß ist. Da ein Teilchen in der quantenmechanischen Beschreibung keinen eindeutigen Aufenthaltsort hat, sondern mit einer gewissen Wahrscheinlichkeit überall zu finden ist, besteht auch eine gewisse Wahrscheinlichkeit, dass sich zwei Protonen nahe genug für eine Fusion kommen; die abstoßende Barriere der elektrischen Kräfte wird also quasi durchtunnelt.
So oder so: Am Ende ist aus vier Wasserstoffkernen ein Heliumkern geworden. Dieser Heliumkern hat ein bisschen weniger Masse als die beiden einzelnen Wasserstoffkerne zusammengenommen. Die überschüssige Energie ist die, die bei der Fusion abgegeben wird. Nimmt man alle Reaktionen zusammen, bleiben am Ende knapp 25 Mega-Elektronenvolt, die im Inneren der Sonne frei werden. Das klingt viel, ist aber eigentlich ziemlich wenig. In einem halben Liter Bier oder einem 50-Gramm-Riegel Schokolade stecken ungefähr 250 Kilokalorien. Das sind 6500 Billiarden Mega-Elektronenvolt! Oder anders gesagt: 1040 Billiarden Wasserstoffkerne müssen zu 260 Billiarden Heliumkernen verschmelzen, damit die gleiche Menge an Energie frei wird, die in einem großen Glas Bier oder einem kleinen Schokoriegel steckt. Aber das ist kein Problem: In jeder Sekunde werden in der Sonne 564 Millionen Tonnen Wasserstoff in 560 Millionen Tonnen Helium umgewandelt und vier Millionen Tonnen ihrer Masse in Energie. Das ist genug für einige Gläser Bier… für ein 343 Trillionen pro Sekunde um genau zu sein.
Aber noch ist die Energie im Kern gefangen. Bis sie zu uns auf die Erde gelangt, hat sie noch einen weiten Weg vor sich. Aber dazu dann mehr in der nächsten Folge der Sternengeschichten.

Zitat: „So oder so: Am Ende ist aus zwei Wasserstoffkernen ein Heliumkern geworden“ – ist in dieser Rechnung nicht ein Fehler? 2*1H wird zu 4He?
In der oben beschriebenen Proton-Proton-Reaktion passiert doch 2*(3*1H->3He)->4He+2*1H, also 4*1H->4He. Die Rechnung mit dem Bier ist dann wohl ebenso falsch (500… -> 250…).
@Georg: „Am Ende ist aus zwei Wasserstoffkernen ein Heliumkern geworden” – ist in dieser Rechnung nicht ein Fehler? 2*1H wird zu 4He?“
Ich hab damit nicht die Reaktion an sich beschrieben, sondern den Effekt. Aus zwei Wasserstoffatomen wird ein Heliumatom (und dazwischen passiert natürlich noch jede Menge anderes Zeug)
Und mit Ausnahme geothermischer Energie.
Geothermische Energie ist zu einem großen Teil „Kernergie“, genauer: Die Wärme aus dem radiaoktiven Zerfall von – wenn ich mich richtig erinnere – hauptsächlich Thorium und Uran.
Ansonsten gibts da noch bewegtes Wasser durch Gezeiten – da kommt die Energie hauptsächlich aus der Erdrotation. Fällt aber im großen und ganzen auch nicht wirklich ins Gewicht.
@Richard: „Ansonsten gibts da noch bewegtes Wasser durch Gezeiten“
Für die zu einem nicht unwichtigen Teil auch die Sonne verantwortlich ist 😉
@Florian
Ich komme auch auf 4 H1 -> 1 He4. Aus 4 Protonen (+4 rumschwirrende Elektronen) des Wasserstoffs werden 2 Protonen, 2 Neutronen und 2 Elektronen (die übrigen 2 lösen sich mit den 2 Positronen in Energie auf) – und 2 Neutrinos und Energie.
@Ambivalent: Du hast recht. Da hab ich tatsächlich was durcheinander gebracht.
„oder einem 50-Gramm-Riegel Schokolade stecken ungefähr 1000 Kilokalorien.“
Ist sicherlich nicht so wichtig, aber gemeint sind kJ,oder?
1g Fett entspricht 9,3 kcal oder 39 kJ.Die meisten Arten von Schokolade haben einen physiologischen Brennwert zwischen 2.100 und 2.500 kJ pro 100 Gramm (= 500 bis 600 kcal),demzufolge 50 Gramm um die 1000kJ- 1250kJ.
@Anderer Michael: Hmm – ich meinte, das in 50g Schoko ca 250 kcal stecken; so wie in 0,5L Bier. Schon der zweite Zahlendreher in dem Text; da war ich wohl unkonzentriert (lag sicher an ner Gravitationswelle)
Schöne Sternengeschichte!
Was ich allerdings immer noch nicht ganz verstehe: Wie kommt der Tunneleffekt genau zustande?
Liegt das wirklich nur an den „Aufenthaltswahrscheinlichkeiten“, die Schrödinger berechnet hat?
Den Vergleich mit dem Bier finde ich übrigens klasse. Gleich mal zum Kühlschrank, gucken ob noch Energie da ist….
Wenn man das Bier in seine Elemente zerlegen würde und sie den gleichen Bedingungen, wie sie im Innern der Sonne herrschen, aussetzen würde….da wäre ein halber Liter mit Sicherheit zu erstaunlichen Dingen imstande 🙂
Woher hat der Stern denn das Barium? Ba ist ein sehr schweres Element (deshalb heißt es ja auch so), vieeel schwerer als Eisen, und entsprechend selten. Glaubt man Wikipedia, dann kommt im Sonnensystem auf 10¹² Atome H gerade mal ein Ba-Atom.
Sicher, daß an dieser Stelle nicht von Bor die Rede ist?
Ich finde es etwas unfair, daß Du hierein einzelnes He-Atom gegen eine makroskopische Menge chemischen Treibstoff antreten läßt. 25 MeV pro gebildetes He-Atom sind für chemische Verhältnisse eine gigantische Energie, eine Million mal mehr als beim Verbrennen eines Moleküls Glucose frei wird (allerdings hat so ein Molekül 24 Atome, und nur ein Teil der 2.8 MJ/mol Energie kann vom Körper genutzt werden).
Oder anders gesagt: die 5·10¹⁷ H-Atome wiegen ungefähr ein Mikrogramm, also größenordnungsmäßig so viel wie ein Kristall Speisesalz. Und sie liefern gleich viel Energie wie ein Glas Bier.
@Chemiker: Ach verdammt; natürlich ist es Bor und nicht Barium. Hab nur das „B“ in der Gleichung falsch übersetzt. Das kommt davon, wenn man zwischen der ganzen Reiserei zwischen Österreich und Deutschland auch noch Podcasts schreibt. Bei der Folge war ich wohl wirklich zu unkonzentriert. Stimmt denn wenigstens jetzt alles? Dein Vergleich mit dem Salzkristall ist auch recht schön; aber die 1000 Billiarden H/250 Billiarden He-Atome stimmen auch? Ich will das Material demnächst für ne andere Sache verwenden und da sollte ich ein paar Vergleiche zur Auswahl haben…
[…] Energie durch Kernfusion in ihrem Inneren. So viel ist klar und so viel habe ich auch schon in der letzten Folge erklärt. Aber wie kommt die Energie aus dem Kern wieder heraus und bis zu Erde? Das klingt […]
„564 Millionen Tonnen Wasserstoff in 560 Tonnen Helium“
Hier fehlt noch ein „Millionen“
Ich hatte das alles nur π mal Tangens Daumen runtergeschätzt, jetzt eine genauere Rechnung, mit ein paar Zwischenschritten und allen verwendeten Zahlen. Ein Mol hat 6·10²³ Atome/Moleküle/Wasauchimmer, und 1 eV entspricht 96485 J/mol (der Teufel soll dieses Chaos mit den Energie-Einheiten holen). Deine Schokolade liefert 1050 kJ pro 50 g.
Laut Wikipedia hat die p-p-Reaktion (pp I branch) eine Gesamtenergie von 26.7 MeV bzw. 2.58 TJ/mol (bezogen auf das He, pro Proton ist es dann nur ein Viertel).
Die Verbrennungsenergie von Glucose ist 2.81 MJ/mol, also ungefähr ein Millionstel davon. Ein Glucose-Molekül (M=180 g/mol) ist aber ca. 45 mal schwerer als ein Heliumkern bzw. vier Protonen. Glucose hat die Formel C₆H₁₂O₆, daher besteht ein Molekül aus 24 Atomen.
50 Gramm Glucose sind 0.28 mol bzw. 0.17·10²⁴ Moleküle (aus 4·10²⁴ Atomen) und liefern also ca. 780 kJ Wärme. Dasselbe wird von 300 nmol He (eigentlich 1.2 µmol Wasserstoff) erbracht — das sind 1.2 µg oder 180·10¹⁵ He-Atome.
Bei der Bildung von 180·10¹⁵ (sind das Billiarden?) He-Atomen bzw. 1.2 µg entsteht also gleich viel Energie wie bei der Verbrennung von 50 g Glucose, was ungefähr 40 g Schokolade entsprechen dürfte.
Salz hat eine Dichte von 2.1 g/cm³. Pro Kubik-Millimeter sind es also 2.1 mg, ein Würfel mit einem Zehntelmillimeter Kantenlänge würde 2.1 µg wiegen (das ist klein, aber mit freiem Auge noch zu sehen). Das wäre dann ungefähr der richtige Größenbereich als Vergleich für unsere 1.2 µg Helium.
Ich habe auf die Schnelle keine Angabe für die Größe von handelsüblichen Salzkristallen gefunden, würde sie aber auf 0.3 bis 0.5 mm Kantenlänge schätzen. Das wären dann grob 100 µg.
Ein Beispiel: Salzkristall mit 0.36 mm Kantenlänge als Vergleichsobjekt … 100 µg … 25 µmol He … 15·10¹⁸ He-Atome … 64 MJ Fusionsenergie … 23 mol Glucose (14·10²⁴ Moleküle bzw. 330·10²⁴ Atome) … 4.1 kg Glucose bzw. 3.1 kg von Deiner Schokolade.
Oder wir beginnen mit der Schokolade und rechnen alles darauf um: 50 g Schokolade … 1.05 MJ … 0.37 mol Glucose (67 g, 0.22·10²⁴ Moleküle, 5.4·10²⁴ Atome) … 0.41 µmol He (244·10¹⁵ He-Atome) … 1.63 µg He … entspricht einem Salzkristall von 0.092 mm Kantenlänge.
Ich hoffe, daß da keine Rechenfehler drin sind.
In jedem Fall sieht man: Die Kernreaktion liefert pro Atom oder auch pro Gramm ein paar Millionen mal mehr Energie als chemische Reaktionen, so als Faustregel.
@Chemiker: Danke!
@Carsten:
Ja.
Das ist eine putzige und unintuitive Spezialität der Quantenmechanik, die aber inzwischen (meint in den letzten ca. 70 Jahren) interessanterweise zu jeder Menge technischer Anwendungen geführt hat.
Das ist also nicht nur eine Theoretische Sache, die man zur Beschreibung der Vorgänge im Inneren von Sternen braucht.
Guckst du:
https://de.wikipedia.org/wiki/Tunneleffekt
@Chemiker:
Das hast du aber schön vorgerechnet!
*hierisdeinschokokeks* :-).
Nein im Ernst: Schöne quantitative Abschätzung! Ich mag sowas und lese sowas immer wieder mit wachsender Begeisterung!
@PDP10: Danke sehr!
Faszinierend, was damit alles möglich ist.
Hallo Florian: Du schreibst
„In jeder Sekunde werden in der Sonne 564 Millionen Tonnen Wasserstoff in 560 Millionen Tonnen Helium umgewandelt und vier Millionen Tonnen ihrer Masse in Energie.“
Wie kommst du auf diese Zahlen? Ich habe sie, so glaube ich, woanders schon mal gesehen.
Nur erscheinen mir sie zu klein.
In der englischen Wikipedia steht etwas von 620 Millionen Tonnen Wasserstoff die umgewandelt werden.
https://en.wikipedia.org/wiki/Sun#Core
Falls ich annehme, dass die gesamte Energie aus der Wasserstofffusion stammt komme ich auf 610,2 Millionen Tonnen Wasserstoff, die pro Sekunde in 605,9 Millionen Tonnen Helium umgewandelt werden.
Woher ist die Diskrepanz?
Vielleicht ist das nur im Rahmen der Messgenauigkeit? Die Beobachtung der Sonne muss naturgemäß aus weiter Entfernung erfolgen.
Ich muss wieder einmal Widerspruch anmelden. Natürlich nicht bei der Fusion als solcher, aber bei ihrer Darstellung als stellare Energiequelle.
Denn Fusion kommt ja, ganz wie Florian beschreibt, nur zustande, weil so enorme Drücke und Temperaturen im Kern herrschen, und die sind das Endresultat des Kollaps einer Gaswolke unter der eigenen Gravitation (›Fahrradpumpe‹). Ohne sie würde der Stern einfach immer weiter kollabieren, Druck und Temperatur würden einfach weiter steigen, das Gas würde immer stärker glühen und die umgewandelte potenzielle Energie abstrahlen. Kurz gesagt: der Stern würde immer kleiner und heißer. Gäbe es keine Fusion, würde die Gaswolke ohne Umweg über die Hauptreihe im HR-Diagramm direkt zum weißen Zwerg zusammenfallen (im wahrsten Wortsinn).
Dass Fusion einsetzt, /bremst/ diesen Vorgang lediglich, indem abgestrahlte Energie auf einmal durch umgewandelte Masse ersetzt wird. So betrachtet verhindert die Fusion die schnellere Kontraktion und die damit verbundene Aufheizung; überspitzt könnte man sagen, sie /kühlt/ den Stern.
Aber die eigentliche Energiequelle ist der Gravitationskollaps der Sternmasse, nicht die Fusion in seinem Inneren.
@#20 (ohne jetzt die Zahlen nachgerechnet zu haben): aus der Massedifferenz des Fusionsprozesses. Wenn ein Prozess die Energie e freisetzt, muss das Endprodukt gemäß Einstein um die Masse m=e/c² leichter sein.
@#20: meine vorige Antwort #23 löschen, bitte, das war Quatsch, ich habe die Frage nicht richtig gelesen.
Ich nehme an, die Diskrepanz kommt daher, dass alles, was wir wissen, ja ›bloß‹ aus Modellrechnungen stammt. In einen Stern hinein schauen kann ja keiner, und auf eine Waage legen können wir die Sonne auch nicht. Und bei unterschiedlichen Modellen wird es Unschärfen geben, vermute ich.
Was trotz- und alledem nichts daran ändert, dass das Wasserstoff- und ggf. Helium-, Kohlenstoff-, Neon-, Sauerstoff- und Siliziumbrennen für den Hauptteil der Energiefreisetzung in einem Stern verantwortlich ist. Ein Weißer Zwerg glüht dagegen nur noch nach, das dann zugegebenermaßen aber noch ziemlich lange (falls er nicht doch noch per Akkretion zur Supernova vom Typ Ia wird).
Matthias Wolf # 22,24,24
1, Selbstverständlich besteht unser gesamtes Weltbild nur aus Modellen, je weiter Du in die Naturwissenschaften einsteigst, desto modellhafter wird das ganze.
Aber jetzt mal zu Deinem Hauptpunkt, dass die Hauptenergiequelle der Sonne die Wärme durch Kompression der Gase ist (adiabatische Kompression). Das kannst Du selber nachrechnen, habe ich auch gemacht vor mehr als 30 Jahren in den Physikübungen an der Uni. Das haben auch andere schlaue Leute gemacht, Helmholtz, Lord Kelvin etc.
Das Problem ist dabei, dass DIESES Modell einfach nicht stimmig ist. wie gesagt, es sei an Dir das selber einmal durchzurechnen.
Du kannst dann selbstverständlich auf Deinem, bzw auf Kelvins (hat er ja schon vor Dir postuliert) Modell bestehen, dann hast Du aber das Problem, jede Menge andere Fakten schlicht zu leugnen. Der elegantere Weg wäre, Du akzeptierst, dass die Kompressionswärme keine Rolle spielt beim Strahlungshaushalt der Sonne.
Bedenke immer, Dein Modell ist etwa 150 Jahre alt, ich glaube man hat seitdem ein wenig gelernt.
Captain E., Folke Kelm & Alderamin, Joker:
Vorab: die Einwände sind richtig! Und irgendwie auch wieder nicht, aber dazu unten mehr. Ich gebe aber unumwunden zu, dass ich unsorgfältig formuliert habe.
Stellen wir außer Streit: die über die Lebensdauer abgestrahlte, kumulierte Energiemenge kommt hauptsächlich aus dem Massendefekt der diversen Fusionsvorgänge. Und so betrachtet ist die Hauptenergiequelle ganz eindeutig die Fusion.
Die Erklärungen allerdings, die dann folgten, habe ich so verstanden, dass es in der Sonne heiß ist, weil dort Fusion statt findet. Aber diese oft gebrachte Erklärung ist eben falsch (und Florian hat das auch nicht gesagt, wie ich beim nochmaligen Lesen festgestellt habe!) Richtig ist nämlich das Gegenteil: in der Sonne findet Fusion statt, weil es dort heiß ist. (Das /hat/ Florian gesagt!)
Denn hier kommt eben eine etwas andere Betrachtungsweise ins Spiel: wenn jemand von der ›Energiequelle‹ redet und damit die /kumulierte/ abgegebene Energie meint, so ist die Aussage völlig richtig, dass die Fusion die Quelle ist. (Mit der gesamt abgegebenen Energiemenge bzw. der Lebensdauer hatten ›Helmholtz et al.‹ Schwierigkeiten, nicht mit der Temperatur. Die lässt sich mit Kontraktion spielend erklären.)
Wenn man aber nur den Moment betrachtet und fragt: wieso ist die Sonne so heiß, wie sie ist, so spielt die Fusion dabei /keine/ Rolle, denn die Temperatur kommt aus der Kontraktion. Und das meinte ich mit ›Quelle‹. (Vermutlich nicht wenige Hörer denken bei ›der Energiequelle‹ an die augenblickliche Temperatur und nicht an die Gesamtmenge. Bei der E-Herdplatte sind die beiden Quellen identisch, beim Stern nicht.)
Die Fusion ist ›lediglich‹ der Mechanismus, der sie so lange aufrecht erhalten kann, indem sie abgestrahlte Energie ersetzt und so verhindert, dass sich der Stern weiter zusammenzieht und dabei noch weiter aufheizt (jedenfalls, bevor Materie ›entartet‹ und Dichte, Druck und Temperatur entkoppelt werden – aber davon ist ja bei der Sonne nicht die Rede).
Nein, das ist eben gerade nicht so. Waren wir und darüber nicht bereits einig geworden? Der Massedefekt der Kernfusion sorgt für wirklich eine Menge an freiwerdender Energie. E = cmc (unter Vermeidung von „hoch zwei“).
Räum ich ja oben ein, oder? Jedenfalls täuschst Du Dich, denn die beiden Dinge widersprechen einander nicht. Sie betrachten nur andere Aspekte (Gesamtenergiemenge / Aufheizung). Wie auch immer: Details nachzulesen im u.a. Textbuch (*sehr* empfehlenswert!). Ich denke mir das nicht aus, wenn ich etwas sage.
Ryan, S.G., Norton, A.J. ›Stellar Evolution and Nucleosynthesis‹, Cambridge University Press, 2010, ISBN 978-0-521-13320-3, https://www.cambridge.org/9780521133203
Sogar die Textstelle habe ich gefunden – Ch. 2.6 Why are Stars hot? Putting fusion in its place:
»Stars are hot because they have collapsed from large diffuse cloud, and gravitational potential energy has been converted to kinetic energy. That is why stars are hot. The role of nuclear fusion is to delay the collapse for long enough that planets, human life and astrophysics courses could develop.«
@Matthias Wolf:
Keiner von denen, mit denen Du hier diskutierst, geht davon aus, dass sich Sterne erst durch Fusion aufgeheizt haben.
Für mich lesen sich Deine Kommentare wie ein Rückzugsgefecht, weil Du komplett falsch lagst mit #22.
Krypto, wie sich meine Kommentare für Dich lesen, geht mir eigentlich völlig hinten vorbei. Dass ich unsorgfältig formuliert habe, habe ich in #27 gleich am Anfang gesagt. Dann habe ich auf die gültige Aussage eingeschränkt und belegt.
Wenn das jemand nicht zur Kenntnis nimmt, ist das weder meine Schuld noch mein Schaden.
Eigentlich also nichts mehr zu tun, so lange kein Argument jenseits von ›du liegst falsch‹ gebracht wird.
@ Matthias Wolf
„astrophysics courses could develop“
Okay, danke für die Erläuterungen. Ich glaube, verstanden zu haben, und denke tatsächlich, wir liegen gar nicht mehr auseinander. In #22 war mit ’stellarer Energiequelle‘ nicht das gemeint, was ich unterstellt hatte.
Die durch Fusion gewonnene, nach außen gerichtete Strahlungsenergie verhindert, dass der Stern sich durch Kontraktion weiter aufheizt. Interessante Sichtweise, nicht unlustig. So deutlich formuliert war mir das noch nicht bewusst. Wieder was gelernt.
Danke, Joker! (Und: bitte, gern geschehen!)
Bis zum Beweis des Gegenteils, der Hausherr kann dazu bestimmt etwas sagen, gehe ich allerdings davon aus, dass die durch Gravitationskollaps zu erzielende Energie um einiges geringer ausfällt als die, die die durch Kernfusion frei wird.
@Captain E.
Das sagt er doch (#27)… Er sagt nur, dass der Stern heiß genug zur Fusion wird, weil die Kontraktion die nötige Aufheizung liefert. Die würde sogar noch eine Weile weiter heizen, wenn die Fusion nicht starten und den Kollaps durch ihren Strahlungsdruck verzögern würde.
Erlischt eine Fusionskette (z.B. Proton-Proton-Kette), dann kontrahiert der Stern wieder und wird noch heißer, bis die nächste Kette zündet usw. So gesehen ist die Kontraktion die Heizung. Wie beim Dieselmotor. Selbstzünder.
Danke, Alderamin. Der Diesel als Selbstzünder ist schön! Das werde ich mir klauen, wenn’s recht ist.
@Alderamin:
Aber nur mit einem ziemlich großen „Ja, aber…“. Ich sehe da in seinen Ausführungen immer noch ein „Primat der Kontraktionswärme“, um das einmal so zu nennen. Dabei geht es ja nun wirklich lediglich um die Bedingungen, die im Inneren eines Sterns notwendig sind, um die Kernfusion zu starten. Dabei unterschlägt Matthias sogar noch den durch die Kontraktion hervorgerufenen Druck. Dieser stammt nun wirklich nur aus der von der eigenen Masse des Sterns verursachten. Die Kernfusion generiert bekanntlich einen Strahlungsdruck, der dagegen wirkt. Und die Wirkung des Drucks ist nicht zu unterschätzen. Da wir diesen in unseren Fusionsreaktoren nicht auch nur annähernd nachbilden können, müssen wir zu noch einmal erheblich höheren Temperaturen greifen, um überhaupt Atome zur Fusion anzuregen. (Und ja, die Temperaturen im Inneren der Reaktoren haben tatsächlich nichts mit der Kernfusion zu tun, aber ein Reaktor ist halt keine Sonne.)
@Captain E.
Na ja, Druck und Temperatur hängen ja direkt (adiabatisch) zusammen.
Ich gehe davon aus, dass der Stern durch den Start der Fusion innen auch heißer wird, als er es vor dem Zünden war, denn es besteht ja eben kein adiabatischer Zustand mehr, wenn Energie ins Gas hinein gepumpt wird, insofern heizt ihn dann auch die Fusion von innen auf und kühlt ihn nicht etwa ab. Es wird lediglich die Kontraktion als Energiequelle temporär gestoppt.
»Ich sehe da in seinen Ausführungen immer noch ein “Primat der Kontraktionswärme”, um das einmal so zu nennen«
@Captain E.: Du siehst es vielleicht, aber zu unrecht. Oder wie verstehst Du meinen Satz (#27): »Vorab: die Einwände sind richtig! … Stellen wir außer Streit: die über die Lebensdauer abgestrahlte, kumulierte Energiemenge kommt hauptsächlich aus dem Massendefekt der diversen Fusionsvorgänge. Und so betrachtet ist die Hauptenergiequelle ganz eindeutig die Fusion.« Danach rede ich von der Energiequelle für die A̲u̲f̲h̲e̲i̲z̲u̲n̲g̲.
Kein ›ziemlich großes Aber‹ also. Alderamin hat ganz genau zusammengefasst. Auch unterschlage ich keineswegs Druck – bitte lies genau, bevor Du widersprichst. Sonst machst Du denselben Fehler wie ich eingangs.
Ich empfehle nochmals das wirklich gute Buch
Ryan, S.G., Norton, A.J. ›Stellar Evolution and Nucleosynthesis‹, Cambridge University Press, 2010, ISBN 978-0-521-13320-3, https://www.cambridge.org/9780521133203
@Alderamin: nein, der Stern wir nicht heißer, wenn die Fusion einsetzt! (Jedenfalls nicht laut dem Standardmodell.) Das ist ja der Punkt, um den es geht: er ist im (bzw. sehr nahe am) hydrostatischen Equilibrium, und die FUsion ersetzt exakt die abgestrahlte Energie und stoppt daher die Kontraktion! Würde er heißer, müsste er sich aufblähen.
(@Captain: das dürfte widerlegen, dass den meisten der Zusammenhang klar ist.)
@Alderamin: die Gleichung für das Hydrostatische Gleichgewicht ist:
Tc ∝ Mµ/R
Tc … Kerntemperatur
M … Masse
µ … Metallizität
R … Radius
Sonst geht da nichts ein. Der Gedankengang: wir wissen, dass der Hauptreihenstern *sehr*, sehr nahe beim h.E. arbeitet. Wir wissen auch, dass der Protostern sehr nahe am h.E. zusammenfällt. Das Eine geht ins andere über, und der Stern ist geboren (Beim Übergang wird’s schon ein paar Oszillationen geben, aber der gezündete Stern leuchtet nicht auf, oder? Das müsste er aber.)
@Matthias Wolf
Das muss aber eine grobe Näherungsformel sein. Hier auf Seite 20 stehen die Grundgleichungen des Sterns, und da hängt T auch von der Energieproduktion L ab. 2 Seiten weiter wird dann aber der Druck und die Temperatur im Inneren der Sonne mit einem vereinfachten Modell, das die Energieerzeugung nicht berücksichtigt, berechnet. Der berechnete Druck ist zwei Größenordungen zu klein, aber die Temperatur stimmt ungefähr.
@Alderamin, die Gleichung kann ich herleiten (s.u.), aber vorher zu Deinen Folien: dort steht eigentlich genau, was ich meine, wenn auch nicht so explizit:
Seite 2:
»The star is stabilised (i.e. nuclear reactions are kept under control) by a pressure-temperature thermostat.«
Seite 3:
»Suppose the fusion rate increases, then
* temperature increases
* pressure increases
* core expands
* density and pressure decrease
* fusion rate decreases«
Seite 4:
»* Suppose that there was no energy generation in the core. The pressure would still be high, so the core would be hotter than the envelope.
* Energy would escape (via radiation, convection,…) and so the core would shrink a bit under the gravity
* That would ̲m̲a̲k̲e̲ ̲i̲t̲ ̲e̲v̲e̲n̲ ̲h̲o̲t̲t̲e̲r̲«
Und unten:
»In stars, nuclear fusion plays this role.«
Hier die Herleitung der Gleichung:
Das Gesetz für ideale Gase lautet
P(r) = ρ(r) kT(r) / m̅
P(r) … Druck in Entfernung r vom Mittelpunkt
ρ(r) … Dichte in Entfernung r vom Mittelpunkt
k … Boltzmannkonstante
T(r) Temperatur in Entfernung r vom Mittelpunkt
m̅ … durschnittliche Masse eines Partikels im Stern
Aufgrund der Homologieannahme können wir davon ausgehen, dass dP(r) (Druckänderung) gleich skaliert wie Pc (Druck im Mittelpunkt), ein radiales Intervall dr und r skalieren gleich wie der Oberflächenradius R. m(r) (die von r eingeschlossene Masse) skaliert wie die Gesamtmasse M und ρ(r) skaliert wie der durchschnittliche Druck ϼ (ich habe kein überstrichenes ρ im Zeichensatz).
Das erlaubt uns, eine Skalierungsrelation für den Druck im Mittelpunkt aufzustellen:
Pc ∝ ϼTc / µ
Die 4 Gleichungen für die Sternstruktur (Deine Folie 20) können wir gleich außer Streit stellen: ich habe hier die gleichen vor mir liegen.
Deine zweite Gleichung ist die des hydrostatischen Equilibriums: dP/dr = – Gmρ / r²
( Bei mir ist sie noch einen Tick detaillierter aufgeschrieben: dP(r)/dr = – Gm(r)ρ(r) / r²
indem Druck, Masse und Dichte als Funktion von r angeschrieben sind.)
Aufgrund der Homologieannahme skaliert der Druck P(r) wie der Druck Pc im Kern, die Dichte ρ(r) wie die Durchschnittliche Dichte ϼ und die Temperatur T(r) skaliert wie die Kerntemperatur Tc (und da wird es interessant).
Die Skalierungsrelation können wir also folgendermaßen aufschreiben:
Pc/R ∝ Mϼ/R²
und weiter
Pc ∝ Mϼ / R
Wir haben jetzt eine Skalierungsrelation für Pc aus der Gleichung für ideale Gase und eine aus dem hydrostatischen Gleichgewicht. Die können wir gleichsetzen und erhalten
ϼTc / µ ∝ Mϼ / R
die durchschnittliche Dichte kürzt sich weg und wir erhalten
Tc ∝ Mµ/R
die Gleichung, die ich vorhin gegeben habe.
Ich schnalls nicht: was sind das für Umwandlungen? Ich kann mit dem Begriff Skalierungsrelation nichts anfangen. Ich glaube ich sehe, was da jeweils in was umgewandelt wird, aber wieso verschwinden zB k und G? Kann das jemand erklären?
@Dobby: gerne. Du hast ganz richtig erkannt, dass für die Skalierungsrelation eine Gleichung umgewandelt wird, indem bestimmte Terme einer Gleichung durch andere ersetzt werden. Vor allem aber wird das = durch ∝, die Proportionalität (wie in Volumen ∝ Kantenlänge³ ) ersetzt!
So etwas kann interessant sein, wenn man sich nicht in den Details einer Gleichung verheddern will, sondern grundsätzliche Aussagen braucht (bei uns bspw. die Frage: geht die Energieproduktion in die Temperatur ein?)
Allerdings sind die Ersetzungen alles andere als beliebig: Du musst Dich an genaue Regeln halten. Im Fall von Hauptreihensternen (die durch die 4 Grundgleichungen beschrieben werden, die Alderamin in #43 verlinkt hat) kannst Du u.a. die Ersetzungen vornehmen, die ich im Text genannt habe. Dadurch werden bspw. P(r) (der Druck an einer Stelle), dP(r) (die Druckänderung an einer Stelle) durch P(0) ersetzt (ich habe geschrieben Pc, der Druck im Zentrum), wodurch die Relation schon einmal deutlich weniger verschiedene Ausdrücke enthält und einfacher wird. Was noch dazu kommt: ›Relation‹ sagt ja nur etwas über Verhältnisse aus, nicht über absolute Größen! Damit aus einer Relation eine Gleichung wird, müsste man einen ›Proportionalitätsfaktor‹ einführen: A∝B gilt für alle Gleichungen A=B, A=2B, A=5B usw. (die Proportionalitätsfaktoren sind hier 1,2,5.)
Solche Details interessieren uns aber gerade /nicht/, wir wollen nur wissen, wie sich die Temperatur irgendwo verhält, wenn sie im Zentrum auf das Doppelte steigt. Und gemäß der Skalierungsrelation steigt sie an jeder anderen Stelle im Stern auch auf das Doppelte. Deswegen kann man konstante Ausdrücke weglassen: sie werden vom (in einer Relation nicht angeschriebenen) Proportionalitätsfaktor ›verschluckt‹.
Warum funktioniert das? Das funktioniert in diesem Fall eben aufgrund der 4 Grundformeln für die Sternstruktur. Die beschreiben die innere Strukur eines Sterns, und aus denen geht hervor, dass sich verschiedene Größen ganz analog zu einander Verhalten (eben unsere Ersetzungen). Das, gemeinsam mit den anderen erwähnten Eigenschaften, ist die ›Homologieannahme‹.
@Matthias Wolf
Danke übrigens für die Herleitung. Scheinst recht zu haben, soweit ich das überblicken kann.
Gerne! (Ist natürlich nicht ›meine‹.)