Nichts bewegt sich schneller als das Licht! Das ist eine der großen physikalischen Erkenntnisse des 20. Jahrhunderts. Aber unser Verständnis der Naturgesetze ist nicht für alle Ewigkeiten in Stein gemeißelt, sondern einem stetigen Prozess der Veränderung unterworfen. Je genauer wir die Natur betrachten, desto genauer wird auch unsere Beschreibung. Als Albert Einstein vor fast 100 Jahren intensiv über Gravitation nachdachte, fand er am Ende ein Modell, das die Realität ein klein wenig genauer beschrieb als die Gravitationstheorie von Newton. Und in 100 Jahren wird vielleicht jemand anderes zeigen können, dass man eine noch bessere Annäherung an die Natur als Einstein finden kann. Mit der Lichtgeschwindigkeit als Geschwindigkeitslimit könnte es vielleicht ähnlich sein. Gerade macht eine Arbeit des Physikers Robert Ehrlich die Runde in den Medien („Six observations consistent with the electron neutrino being a tachyon with mass: m2νe=−0.11±0.016eV2“) in der nahegelegt wird, dass Neutrinos sich schneller als das Licht bewegen.
Ich sage sicherheitshalber gleich zu Beginn, worum es in diesem Artikel nicht gehen wird: Um überlichtschnelle Raumfahrt, Warp-Antriebe, freie Energie aus dem Nichts und ähnliche Grenzgebiete der Science-Fiction und Pseudowissenschaft. Es geht um Elementarteilchen und theoretische Physik – aber die Sache ist trotzdem äußerst interessant.

Neutrinos sind sehr faszinierende Elementarteilchen. Sie wurden 1930 vorhergesagt und 1956 nachgewiesen. Sie interagieren so gut wie gar nicht mit normaler Materie (Neutrinos sind „dunkle Materie“, das heißt sie senden keine elektromagnetische Strahlung aus und absorbieren sie auch nicht sondern interagieren nur über die schwache Kernkraft mit dem Rest der Materie). Wir haben aber mittlerweile gelernt, sie trotzdem zu registrieren (siehe hier und hier) und diese Teilchen verraten uns viel darüber, was im Universum vor sich geht.
Eine der immer noch ungelösten Fragen bei diesem Thema ist die Masse der Neutrinos. Ursprünglich dachte man, sie hätte gar keine Ruhemasse; so wie zum Beispiel auch die Photonen des Lichts. Und als masselose Teilchen würden sich die Neutrinos dann auch mit Lichtgeschwindigkeit bewegen. Diverse Experimente und theoretische Überlegungen haben aber mittlerweile zu der Überzeugung geführt, dass sie doch eine sehr, sehr kleine Ruhemasse besitzen und daher auch ein klein wenig langsamer als das Licht sind. Der genaue Wert der Masse ist allerdings noch unbekannt.
Und hier kommt die Arbeit von Robert Ehrlich ins Spiel: Er behauptet, die Neutrinos hätten eine imaginäre Masse. Das klingt nicht nur ziemlich seltsam. Das ist auch ziemlich seltsam. Imaginäre Zahlen werden die meisten noch aus dem Schulunterricht kennen. Man hat sie eingeführt, um Gleichungen wie x² = -1 lösen zu können. Mit den „normalen“ Zahlen geht das nicht, denn egal ob man eine positive oder eine negative Zahl mit sich selbst multipliziert; am Ende ist das Ergebnis immer positiv. Der Ausweg aus diesem Dilemma waren die imaginären Zahlen. Man hat einfach per Definition festgelegt, dass eine Zahl mit der Bezeichnung „i“ existieren soll, die gleich der Wurzel aus -1 ist. Dann ist i² = -1 und die Lösung für die oben gestellte Gleichung lautet einfach x=i. Mit imaginären Zahlen kann man genau so rechnen wie mit normalen Zahlen und die moderne Mathematik bzw. Physik würde mittlerweile nicht mehr ohne diese Erweiterung des Zahlenraums auskommen. Aber eine Entsprechung in der realen Welt haben die imaginären Zahlen nicht. Was also soll es dann bedeuten, wenn behauptet wird, die Masse der Neutrinos wäre imaginär?
Dazu muss man sich eine der wichtigsten Formeln der speziellen Relativitätstheorie von Albert Einstein ansehen:
Sie beschreibt die Energie eines Teilchens. Die muss immer eine reale, beobachtbare Größe mit einem positiven Wert sein. Und das ist normalerweise auch kein Problem. Ist die Geschwindigkeit v eines Teilchens kleiner als die Lichtgeschwindigkeit c, dann wird in der Formel der Ausdruck unter der Wurzel positiv und der Wert der Energie ist eine normale Zahl. Ist die Geschwindigkeit eines Teilchens aber größer als die Lichtgeschwindigkeit, dann ist die Zahl unter der Wurzel negativ. Und wenn man die Wurzel einer negativen Zahl zieht, bekommt man eine imaginäre Zahl. Damit am Ende die Energie trotzdem eine normale Zahl sein kann, muss als Ausgleich die Masse m über dem Bruchstich ebenfalls eine imaginäre Zahl sein. Dann hat man zwei imaginäre Zahlen, die durcheinander geteilt werden und das Ergebnis so einer Rechnung ist immer eine normale Zahl.
Kurz gesagt: Die Masse eines Teilchens das sich schneller als das Licht bewegt, muss imaginär sein!
Eigentlich könnte man ja denken, man müsste sich mit so etwas gar nicht beschäftigen. Denn immerhin sagt Einstein ja, dass sich nichts schneller als das Licht bewegen kann. Aber das ist nicht ganz korrekt. Seine Theorie besagt nur, dass man unendlich viel Energie benötigen würde, um ein Objekt auf Lichtgeschwindigkeit zu beschleunigen. Es ist also unmöglich, irgendetwas schneller als das Licht zu beschleunigen. Es ist aber – zumindest rein theoretisch – möglich, dass Teilchen entstehen, die schon von Anfang an schneller als das Licht sind! Man kann von Unterlichtgeschwindigkeit nicht zur Überlichtgeschwindigkeit wechseln. Aber Teilchen die sich immer mit Überlichtgeschwindigkeit bewegen, sind kein Widerspruch zur Relativitätstheorie.
Solche hypothetischen Teilchen nennt man Tachyonen (und sie tauchen heutzutage meistens in der Esoterik auf; darum soll es hier aber nicht gehen) und sie haben eine imaginäre Masse. Die Idee, dass es sich bei Neutrinos um genau solche Tachyonen handeln könnte, ist nicht neu – sie ist schon in den 1980er Jahren aufgetaucht. Und tatsächlich gab es früher Messdaten, die damit nicht in Widerspruch standen. Sie lieferten einen negativen Wert für das Quadrat der Masse der Neutrinos, also eine imaginäre Masse. Innerhalb der Fehlergrenzen waren die Werte aber auch mit einer normalen oder gar keiner Masse vereinbar und die Experimente selbst stellten sich später als fehlerbehaftet heraus.
Robert Ehrlich aber hat nun in seiner Arbeit diverse Daten zusammen getragen, die erneut zeigen sollen, dass die Masse von Neutrinos imaginär ist. Eine seiner Überlegungen hat zum Beispiel mit dem „Knie“ in der kosmischen Strahlung zu tun. Die Argumentationskette ist ein wenig knifflig: Es beginnt mit Teilchen, die aus dem Weltraum zur Erde gelangen. Davon gibt es jede Menge; Sterne und andere kosmische Phänomene schicken ständig diverse Teilchen durch die Gegend und wenn sie zu uns auf die Erde gelangen, kann man ihre Energie messen und deren Verteilung aufzeichnen. Tut man das, bekommt man ein Diagramm mit einem „Knie“, also einer Region, in der ein bisschen weniger Teilchen einer bestimmten Energie vorhanden sind, als man eigentlich erwarten würde.
Die Auswertung ist komplex, denn wir wissen immer noch nicht genau über alle Prozesse Bescheid, die kosmische Strahlung produzieren; können also auch nicht exakt sagen, wie viele Teilchen einer bestimmten Energie wir eigentlich erwarten. Aber eine mögliche Erklärung für dieses „Knie“ wären überlichtschnelle Neutrinos. Denn wenn es die gibt, dann folgt daraus unter anderem, dass Protonen nicht stabil sein können. Protonen die sehr hohe Energien haben zerfallen zu Neutronen und Neutrinos und deswegen gibt es weniger davon als man erwarten würde.
Das ist natürlich ein sehr, sehr indirektes Indiz und das gilt auch für die fünf anderen Argumentationslinien, die Ehrlich in seinem Artikel verfolgt. Es handelt sich dabei immer um Messdaten anderer Wissenschaftler, die jede für sich auch ganz ohne überlichtschnelle Neutrinos erklärt werden können. Aber Ehrlich hat die Daten neu und anders ausgewertet und kam dabei zu dem Schluss, das sie alle auf die gleiche und eben imaginäre Neutrinomasse hindeuten, wie dieses Diagramm aus seiner Arbeit zeigt:
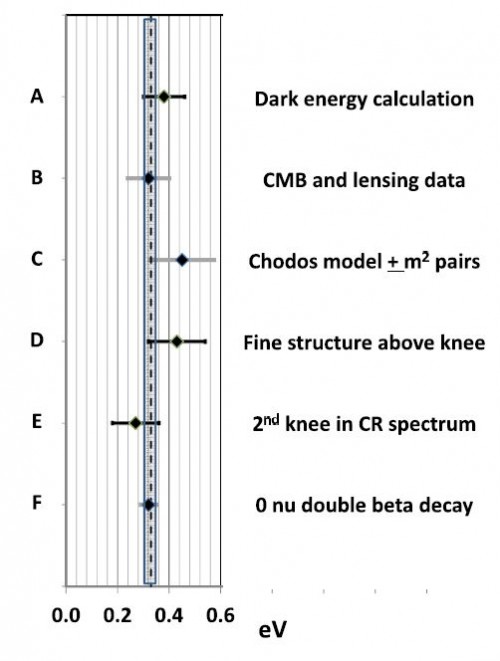
Die sechs Punkte entsprechend seiner Auswertung der Daten und geben die Neutrinomasse an. Innerhalb der Fehlerbalken stimmen sie überein und geben eine Masse an, die imaginär ist und zwei dreimillionstel der Masse eines Elektrons entspricht (mit der angeblichen „Entdeckung“ überlichtschnellen Neutrinos am CERN hat das übrigens erst Mal nichts zu tun; beim CERN ging es um eine andere Art von Neutrinos als denjenigen, mit denen sich Ehrlich beschäftigt).
Man darf ob dieser Behauptung durchaus skeptisch sein. Es ist immer ein wenig schwierig, Experimente im Nachhinein unter anderen Gesichtspunkten zu interpretieren und nicht so zu betrachten, wie sie eigentlich gedacht waren. Und es gibt durchaus auch Argumente, die gegen eine imaginäre Neutrinomasse sprechen. Man sollte dann zum Beispiel eine der Tscherenkow-Strahlung ähnlich Strahlung beobachten können, was man aber nicht getan hat (Tscherenkow-Strahlung entsteht, wenn sich Teilchen in einem Medium schneller als die lokale Lichtgeschwindigkeit bewegen – siehe hier). Mit überlichtschnellen Neutrinos könnte man auch theoretisch rückwärts in der Zeit kommunizieren, was zu allerlei Paradoxien führt weswegen viele Physiker davon ausgehen, dass sie in der Natur nicht existieren können.
Aber natürlich sollte man die Möglichkeit auch nicht völlig ausschließen, solange sie nicht einwandfrei widerlegt ist. Eine imaginäre Masse ist in anderen Bereichen der Teilchenphysik zumindest nicht völlig unbekannt. Bei Quantenfeldern kann es sogenannte „Tachyonenfelder“ geben, die imaginäre Massen haben. Das heißt in diesem Fall aber (sehr vereinfacht gesagt) nichts anderes als dass diese Felder nicht stabil sind, sondern spontan zu einem niedrigeren Energiezustand wechseln können und das bei diesem Vorgang Teilchen entstehen, die dann aber eine normale Masse haben (das Higgs-Feld ist zum Beispiel so ein Tachyon-Feld).
Hätten Neutrinos wirklich eine imaginäre Masse, dann wäre das natürlich eine ziemlich große Sensation. Ihre Masse wäre dann nicht negativ und nicht positiv und auch nicht gleich null. Sie wäre irgendetwas anderes und man müsste sich ein völlig neues Konzept dessen ausdenken, was „Masse“ bedeutet. Solche Paradigmenwechsel gibt es immer wieder in der Physik. Die allgemeine Relativitätstheorie hat ein völlig neues Konzept der Gravitation entwickelt; die Quantenmechanik hat unser Verständnis dessen, was ein „Teilchen“ ist komplett revolutioniert. Wenn ein „Teilchen“ weder ein Teilchen, noch eine Welle ist sondern „etwas“, das eben mal so erscheint wie eine Welle und mal so erscheint wie ein Teilchen; warum soll es dann nicht auch möglich sein, eine imaginäre Masse in unser Modell der Natur einzubauen?

Aber bevor man sich diese Mühe macht, braucht es natürlich zuerst noch mehr und bessere Daten. Die könnten in den nächsten Jahren in Karlsruhe gesammelt werden. Dort wird demnächst das KATRIN-Experiment (Karlsruhe Tritium Neutrino Experiment) gestartet. Dabei wird das sogenannte Betaspektrum des Tritiumzerfalls gemessen. Tritium (ein Wasserstoff-Isotop mit einem Atomkern, der aus einem Proton und zwei Neutronen besteht) ist nicht stabil sondern zerfällt mit einer Halbwertszeit von etwa 12 Jahren. Die Energie der zerfallenden Teilchen wird dabei auf die entstehenden Teilchen aufgeteilt und dazu gehört auch ein Neutrino. Wie genau die Energie aufgeteilt wird, hängt unter anderem davon ab, ob und was für eine Masse das Neutrino besitzt. Misst man also die Energie der beim Tritium-Zerfall entstehenden Teilchen enorm genau, dann kann man daraus die Masse der Neutrinos ableiten. Bis jetzt war so eine Messgenauigkeit nicht möglich, aber der KATRIN-Detektor wird dazu in der Lage sein.
Wenn KATRIN in den nächsten Jahren Ergebnisse liefert, werden wir also besser wissen, ob wir uns tatsächlich Gedanken darüber machen müssen, wie man sich eine „imaginäre Masse“ vorzustellen hat… So oder so – am Ende werden wir auf jeden Fall besser über die Welt Bescheid wissen als vorher und darauf kommt es ja an!
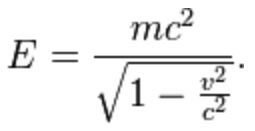
Gilt das alles nur für das Elektron-Neutrino? Und wenn ja, warum?
Grüße
Im aktuellen Bild der Wissenschaft (1/2015) ist ein Artikel der KATRIN anspricht, die messen dort die Maximalenergie der Elektronen dieses Zerfalls und das sich die Energie auf das entstehende Neutrino und das Elektron zufällig(?) verteilt, wäre mit dieser Maximalenergie der Elektronen die Minimalenergie der Neutrinos feststellbar und damit deren Masse.
A) „Imaginäre Zahlen werden die meisten noch aus dem Schulunterricht kennen.“
wirklich die meisten? soweit ich das jetzt im überblick habe kommen die nichtmals im Abitur vor. oder?
B) „Man sollte dann zum Beispiel eine der Tscherenkow-Strahlung ähnlich Strahlung beobachten können“
Ist eine solche Stahlung denn nicht nur für el-mag-WW Teilchen zu erwarten? Dunkle materie sollte es doch egal sein wie schnell em-Wellen lokal sein können, sind ja nicht gekoppelt. und Neutrinos müssen sich ja nicht unbedingt „überschnell“ bewegen, theoretisch gibt es ja anscheinent formal keine grenze für Teilchengeschwindigkeiten.
andernfalls hätten wir doch schon diese Strahlung innerhalb jeder materie, immerhin bewegen sich Neutrinos doch definitiv sehr nahe Lichtgeschwindigkeit und damit schneller als licht in irgendeinem Medium.
C) und kann man wirklich _jedes_ teilchen nicht auf lichgeschwindigkeit beschleunigen, oder gilt das für dunkle materie eben nicht?
D) Ich bin zu meiner eigenen schande auch grade nicht im klaren wie es zur geschwindigkeitsgrenze c überhaupt in der theorie kommt.. wäre es da nicht auch möglich die imaginäre masse durch einen neuen höheren wert für c auszuwechseln? Dann wär Licht zwar das schnellste was sich als em-Teilchen bewegen kann, man hätte dann aber noch luft nach oben für dunkle materie und somit wäre die masse wieder reel.
?
@Zhar: „Ist eine solche Stahlung denn nicht nur für el-mag-WW Teilchen zu erwarten? „
Ja, Tscherenkow-Strahlung. Darum schrieb ich auch „Tscherenkow-ähnliche Strahlung“.
“ Ich bin zu meiner eigenen schande auch grade nicht im klaren wie es zur geschwindigkeitsgrenze c überhaupt in der theorie kommt.“
Die Energie die du brauchst um ein Teilchen zu beschleunigen wächst nicht linear. Du bräuchtest unendlich viel um auf c zu kommen.
@Zhar
A) Weiß ich gar nicht mehr, ob die komplexen Zahlen noch in der Oberstufe kamen oder erst im Studium.
B) Weiß ich auch nicht.
C) Das Limit c kommt aus der Massenzunahme, die für Teilchen mit Ruhmasse bei der Annäherung an c gegen unendlich strebt, d.h. um c zu erreichen, wäre eine unendliche Energie nötig. Man kann nur nahe an c herankommen. Das tut man z.B. in Teilchenbeschleunigern. Die Teilchen dort werden mit zunehmender Beschleunigung kaum noch schneller, aber immer schwerer.
D) Dass Licht sich im Vakuum mit genau c bewegt, folgt aus den Maxwellschen Gleichungen, die eine Beziehung zwischen der elektrischen und magnetischen Feldkonstante einerseits und der Lichtgeschwindigkeit andererseits herstellen (siehe zugehörigen Wikipedia-Eintrag; suche dort nach „Lichtgeschwindigkeit“)
Da muss ich Zhar zustimmen: Meines Wissens gehören komplexe Zahlen in keinem (deutschen) Lehrplan zum Standard-(Pflicht-)Stoff. In einigen Lehrplänen stehen sie wohl als Wahlthema drin – am nach meiner Erfahrung nutzt man die Zeit, die für Wahlthemen vorgesehen ist, meist eher dazu, den Pflichtstoff besser einzuüben…
Zum Thema „direkte Messung der Neutrinomasse über das Spektrum des Beta-Zerfalls“: Ich meine mich daran zu erinnern, dass es mit dieser Methode vor ca. 15 Jahren auch schon mal Hinweise auf eine imaginäre Neutrinomasse gegeben hätte…
@Bjoern, Zhar:2 Meines Wissens gehören komplexe Zahlen in keinem (deutschen) Lehrplan zum Standard-(Pflicht-)Stoff.“
Ok, dann ist das vielleicht in Österreich anders gewesen. Wir haben die auf jeden Fall gelernt und schon relativ früh, wenn ich mich richtig erinnere. Schulstufe 10 oder 11, denke ich.
Kann KATRIN überhaupt imaginäre Massen messen? Zu einer reellwertigen Energie muss doch auch eine reellwertige Masse gehören, und wenn KATRIN misst, welche reellweetige Energie die Elektronen haben, kann doch kein imaginärwertiges Energiedefizit gefunden werden, aus dem eine imaginärwertige Neutrinomasse folgte. Dann käme bestenfalls eine Neutrinomasse von 0 heraus. oder?
@Alderamin: „Kann KATRIN überhaupt imaginäre Massen messen?“
Die messen das Massenquadrat, glaube ich. Aber ich bin da auch kein Experte…
@Zhar, Alderamin:
Im Rahmen der Relativitätstheorien hat c nicht direkt was mit Licht oder Elektromagnetismus zu tun, sondern ist eher eine Art geometrischer Umrechnungsfaktor zwischen Längen in Raum und Zeit. Eine Sekunde ist quasi 299792458 Meter lang. Dass c das Geschwindigkeitslimit für Objekte reeller Masse ist, ist eine Folge dieser Eigenschaft. Licht hat damit nichts zu tun. Daher gilt das Limit auch für nicht-elektromagnetisch wechselwirkende Teilchen. Eine zweites Geschwindigkeitslimit für andere Teilchen ist im bisherigen Theorierahmen nicht möglich (und es ist für mich schwer vorstellbar, wie sowas überhaupt gehen würde; das zweite Geschwindigkeitslimit muss schließlich wie c beobachterunabhängig sein).
Gewissermaßen ist es eher „Zufall“, dass sich Licht mit c bewegt und nicht langsamer. Rein von den Relativitätstheorien her, könnten Photonen auch eine Masse haben. Dann gäbe es immer noch das Limit c, aber keine leicht beobachtbaren Teilchen, die sich mit c bewegen.
@Alderamin:
Soweit ich weiß geht niemand von der Existenz imaginärer Energien aus. Wenn es solche gäbe, müsste man entweder viel am Formalismus der Quantenmechanik ändern (die Zeitentwicklung wäre nicht mehr unitär, was Probleme für die Wahrscheinlichkeitsinterpretation macht), oder dazu noch imaginäre Zeiten einführen (und wenn die Zeit imaginär sein kann, warum dann nicht auch der Raum?).
Die Formel oben in Florians Artikel zeigt doch, dass „Zu einer reellwertigen Energie muss doch auch eine reellwertige Masse gehören“ falsch ist, wenn für das Teilchen immer v > c gilt.
Aber ob KATRIN eine imaginäre Neutrinomasse messen könnte, kann ich nicht sagen.
@alex
Danke. Die Frage B hatte ich allerdings so verstanden, warum überlichtschnelle Neutrinos Tscherenkov-Strahlung aussenden sollten, wo sie doch mit Elektromagnetismus nichts zu tun haben und Tscherenkov-Strahlung elektromagnetische Strahlung ist.
Zum „Zufall“ der Photonengeschwindigkeit, es ist doch kein Zufall, dass c = sqrt 1/(epsilon-0*my-0) ist, oder? Die Felder breiten sich so schnell aus, wie die RT eben erlaubt, ansonsten würde auch im Vakuum ein epsilon-r oder my-r bestehen.
@alex
Zum zweiten Post: stimmt. Die eigentliche Frage war ja, ob man aus der Messung der Energie des Elektrons auf eine imaginäre Masse schließen kann. Aus der Formel ergibt sich eigentlich, dass es für eine gemessene Energie immer zwei Lösungen gäbe, eine mit reeller Masse und Unterlichtgeschwindigkeit und eine mit imaginärer Masse und Überlichtgeschwindigkeit, d.h. KATRIN kann, wenn sie nur die Energien betrachtet, die beiden Fälle dann wohl nicht unterscheiden.
@alex
#(und wenn die Zeit imaginär sein kann, warum dann nicht auch der Raum?).#
so weit ich mich noch ganz dunkel erinnere, ist der Raum der komplexen Zahlen bloss ein Spezialfall eines zweidimensionalen Raums. Dann wäre ein imaginärer, bzw. komplexer (dreidimensionaler) Raum halt einer mit ein drei bzw. vier Zusatzdimensionen.
Find ich nicht so gut den Satz. Was anderes, als eine Entsprechung in der realen Welt, wäre die imaginäre Ruhemasse?
Auch gibts ja schon lang Konzepte in der Kosmogenie die imaginäre Zeit voraussetzen. Und das sind keine unwahrscheinlichen Aussenseitertheorien.
Meiner Meinung nach wäre der Satz so besser:
Wobei du natürlich schreiben kannst was und wie du willst, is nur mein Senf dazu…
Hm, was ist mit Wellenfunktionen?
@Bjoern: „Hm, was ist mit Wellenfunktionen?“
Naja, Wellenfunktionen sind auch nicht unbedingt real 😉 Ich meinte, dass man zB zwar 5 Äpfel haben kann oder 1,5 Bananen aber nicht i Orangen. Das macht einfach keinen Sinn… Dass man mit komplexen Zahlen reale Dinge beschreiben und berechnen kann, steht außer Frage.
@Alderamin:
Ja, zur Frage B von Zhar habe ich auch keine Ahnung. Vielleicht würde die Tscherenkow-Strahlung durch indirekte Kopplung entstehen (Neutrinos koppeln schwach an geladene Leptonen und W/Z-Bosonen und die wiederum an Photonen).
Wenn Photonen massiv wären, würden für sie nicht mehr die Maxwell-Gleichungen, sondern die Proca-Gleichung gelten. Ich denke nicht, dass man die mit einem ϵr und µr in die Maxwell-Gleichungen umformen kann; habe die Rechnung aber nicht versucht.
Die Bestimmung der Neutrinomasse bei KATRIN basiert vor allem darauf, dass Neutrinos mit reeller Masse m mindestens die Energie m c² haben müssen, was die Maximalenergie der Elektronen reduziert. Wenn ich das richtig sehe, sind für imaginäre Masse und Überlichtgeschwindigkeit aber beliebige positive Energien möglich. D.h. die Maximalenergie der Elektronen wäre in diesem Fall die gesamte Zerfallsenergie und man könnte so keine Neutrinomasse bestimmen. Allerdings hätte eine imaginäre Masse vermutlich noch anderen Einfluss auf das Elektronenspektrum.
@Zhar:
Ich denke, in der schwachen Wechselwirkung (der Neutrinos ja unterliegen), müsste es ein Analogon zur Tscherenkow-Strahlung geben.
Interessanter Hinweis. Hm, vlt. gibt es diese Strahlung wirklich, sie ist aber zu schwach, um beobachtbar zu sein? (die schwache Wechselwirkung _ist_ ja schwach 😉 )
@Heino:
Was ich damit meinte: Wenn man die Probleme die imaginäre/komplexe Energien für die Quantenmechanik machen, dadurch löst, dass man auch komplexe Zeiten zulässt, muss man aus Konsistenzgründen auch den Raum komplex machen (R³ durch C³ ersetzen). Und das wäre ein ziemlich großer Eingriff, der Auswirkungen auf viele andere Gebiete hätte, nicht durch Experimente gestützt wäre, und dessen Interpretation (was soll „ein Stock ist (3+2i) Meter lang“ bedeuten?) äußerst unklar ist.
@alex:
schon klar, dass das Ersetzen von R³ durch C³ größere Auswirkungen haben könnte. Allerdings, wenn der Stock bloss (3 + i*10^-30) Meter lang wäre, dann wärs nicht so schlimm.
@Heino:
Ich finde auch (3 + i*10^-30) Meter sehr problematisch. Das Problem ist wie gesagt vor allem eines der Interpretation. Was soll i Meter sein? Längenmessungen basieren doch eigentlich immer auf einer Art Abzählprozess und wie soll man damit auf eine komplexe Zahl kommen?
Ganz zu schweigen von den Problemen einer komplexen Zeit. Solange man keine Produkte betrachtet, wäre das Äquivalent zu zwei reellen Zeiten, mit all den Problemen für Kausalität etc. die das mit sich bringt.
Also natürlich ist das eine Möglichkeit, aber vom wissenschaftstheoretischen Standpunkt ist das schon eine recht heftige Aussage.
Nicht nur dass gut verifiziertes Wissen in Frage gestellt wird (gut, bei Wissenschaft ist die Falsifizierung wichtiger, aber trotzdem, die SRT ist gut etabliert und Erklärungsmächtig), sondern gleich eine Naturkonstante. Und nicht nur das. Es wird zugleich etwas in die Physik eingeführt (also nicht nur formelmäßig, rechnerisch), sondern als physikalische Realität (!), was bisher dort keinen Platz hatte. Damit wird nicht nur eine physikalische Theorie und Naturkonstante in Frage gestellt, sondern gleich auch noch eine neue Realität erschaffen, in der imaginäre Zahlen physikalisch eine Bedeutung haben. Das ist ein starkes Stück.
Meines Wissens gibts dafür andere Theorien, die das pben gestellte Problem erklären ohne unser Weltbild vollkommen über Bord zu werfen. Die Loop Quantum Theory versucht nichts geringeres, als Relativitätstheorie und Quantenmechanik, aber entgegen der Imagniäre-Masse-Theorie oben, ist die sowas von wissenschaftstheoretisch harmlos dagegen …
Und es gilt, um so mehr ich vermutetes Wissen über Bord werfen will, umso erklärungsmächtiger, um so mehr falsifizierbare Aussagen (=Wissen) muss die neue Theorie sein. Würde sich die Theorie der imagniären Masse durchsetzen, wäre das wohl die Theorie der letzten Jahrtausende. Die Theory for Everything wäre ein Lerchalschass, wie wir in Wien dazu sagen, dagegen.
Auch würde ich gerne mal sehen, wie imaginäre Masse und ART zusammen passen. Also okay, imagnäre Masse und SRT lass ich mir noch einreden, aber ob die sich so gut mit der ART vereinabren lässt, muss sich erst zeigen.
@STefan: „Die Theory for Everything wäre ein Lerchalschass, wie wir in Wien dazu sagen, dagegen.“
Wieso soll das so enorm extrem sein? Das verstehe ich jetzt nicht. Es geht ja nicht darum, dass man tatsächlich eine neue Art von „imaginärer“ Materie einführt. Sondern darum, dass es – wenn die Messungen das ergeben sollten – bestimmte Massen nur mit imaginären Zahlen beschrieben werden können. Das bedeutet, dass das Konzept von „Masse“ irgendwie erweitert oder verändert werden muss. Genau das ist ja auch in der Quantenmechanik passiert. Da musste man auch mit dem Welle-Teilchen-Dualismus klarkommen und sich von dem Konzept des „Teilchens“ als konkretes, abgegrenztes „Ding aus Masse“ verabschieden.
@alex
also mir einen Meter vorzustellen habe ich kein Problem. Mir (1+i) Meter vorzustellen habe ich schon kein kleines Problem.
Allerdings habe ich auch kein Problem, mir eine Hundertstel Planck-Länge vorzustellen. Und deshalb frage ich mich, ob ich vielleicht bei der Vorstellung von 1 Meter (reell) doch ein Problem haben sollte!?
Ich will da meine Vorstellungsschwächen nicht zum Maßstab machen, aber
auch die Vor-Einsteinsche Mathematik musste auch gewaltig aufgerüstet werden.
@Heino:
Es geht mir nicht unbedingt um die Vorstellung, sondern darum wie ein komplexer Messwert zu interpretieren sei. Messen ist Abzählen bzw Vergleichen mit Bekanntem. Wenn ein Objekt 3 Meter lang ist, heißt das, dass drei Objekte der Länge 1 Meter hintereinandergelegt dieselbe Länge haben (bzw. dass ein Lichtstrahl im Vakuum zum Zurücklegen dieser Strecke dreimal so viele Schwingungszyklen einer Cs-Atomuhr braucht). Diese Interpretation funktioniert für alle (positiven) rationalen (Verhältnisse von) Messwerten. Für irrationale reelle Zahlen kann man mit rationalen Näherungen arbeiten.
Aber für imaginäre oder nichtreelle komplexe Zahlen funktioniert das überhaupt nicht. Eine Theorie die solche Messwerte vorhersagt, muss also auch sagen, was darunter zu verstehen ist, da das traditionelle Verständnis vom Messen nicht anwendbar ist.
Ein bisschen mehr über Tachyonen und ihre Quantentheorie habe ich übrigens vor einiger Zeit mal geschrieben:
https://scienceblogs.de/hier-wohnen-drachen/2011/09/24/schneller-als-das-licht-tachyonen/
Das ist ein „Aha-Erlebnis“. Mal wieder.
@Florian Freistetter: „Wieso soll das so enorm extrem sein? Das verstehe ich jetzt nicht. Es geht ja nicht darum, dass man tatsächlich eine neue Art von “imaginärer” Materie einführt. Sondern darum, dass es – wenn die Messungen das ergeben sollten – bestimmte Massen nur mit imaginären Zahlen beschrieben werden können.“
Aber genau das ist doch das wesentlich neue. „Normale“ Masse kann ich eben mit reellen Zahlen bbeschreiben. Es wäre was fundamental neues in der Physik, wenn ich Massen nun nicht mehr mit reellen Zahlen beschreiben könnte.
Und einerseits wäre es schon eine Jahrhundert-Sensation, wenn ich Masse ähnlich wie in der Quantenmechanik neu definieren müsste.
Andererseits ist das nicht vergleichbar. Nicht Masse wurde neu definiert, sondern Teilchen. Masse ist ja eine Eigenschaft der Teilchen, die Masse musste nicht neu definiert werden, sondern das Verhalten der Teilchen.
Da würde ich eher noch die Neudefinition im Sinne der RT hernehmen, und den Zusammenhang mit Energie. In Sachen Masse ist die QM eine klassische Theorie und RT hier fortschrittlich. Was aber in diesem Sinne z.B. dann imaginäre Energie sein soll, also Energie, die ich mit imaginären Zahlen beschreibe, wie sich das auf die ART auswirkt, sei mal alles dahingestellt.
Die Theorie wirft nicht nur Überlichtgeschwindigkeit um, sondern fundamentale Vorstellungen unserer Welt. In der Welt der S/ART und der QM. Das allein ist noch nicht schlimm, nur müsste die Theorie derart Beschreibungsmächtig sein, derart viel neue Erkenntnis bringen, denn RT und QM sind erklärungsmächtig. Die in Frage zu stellen, um einen Knick bei hochenergetischen Protonen zu erklären ist mutig … 😉
@Stefan: „Und einerseits wäre es schon eine Jahrhundert-Sensation, wenn ich Masse ähnlich wie in der Quantenmechanik neu definieren müsste.“
Ja, das habe ich im Artikel aber auch erwähnt. Aber bei dir klang es so, als sei das ein extra singuläres Ereignis.
Achso, es kann zwar überlichtschnelle Teilchen geben, aber keinen warp Antrieb ? Aha… vollidiot.
@Hallodry:„Aha… vollidiot“
Ich könnte ja noch ausführlich erklären, warum das so ist (im Artikel ist es aber auch eigentlich schon erwähnt). Aber so wie es aussieht, scheinst du eher nur zum Pöbeln hier zu sein und nicht an einer seriösen Diskussion interessiert.
Verletzung der Lorentz Invarianz wurde in der Geschichte der Menschheit noch nie beobachtet, weil es das einfach nicht gibt. Der Typ ist wahrscheinlich ein üblicher crackpot und es wird sich bald aufklären.
Imaginäre Masse macht keinen Sinn, dann würde es keinen Grundzustand geben, jedenfalls nur einen im labilen Gleichgewicht. Dann wäre übrigens auch die Quantenmechanik am Arsch. Warpantrieb wird ausserdem lokal auch nicht schneller als die Lichtgeschwindigkeit, wobei das ja alles zusammenhängt (aber davon hat er ja keine Ahnung psshhht). Aber dann ist wahrscheinlich die negative Masse die man für den Warpantrieb braucht wahrscheinlich möglich, wenn sie möglich ist damit Neutrinos schneller als Licht fliegen können LOL
@Hallodry: Ok. Noch ne Chance: Willst du ernsthaft diskutieren? (Ich habe hier auch schon über Warp-Antrieb u.ä. gebloggt und demnächst erscheint mein neues Buch, wo es u.a. um genau dieses Thema geht). Wenn ja, dann solltest du dir einen anderen Tonfall suchen. Und probieren zu verstehen, dass es hier um Elementarteilchenphysik geht die erst Mal nichts mit dem Warp-Raumkrümmungszeug zu tun hat. Wenn du aber nur rumpöbeln willst, fliegst du raus. Auf sowas hab ich keine Lust.
Komischerweise sind Sachen wie Warp Antrieb pseudowissenschaft, aber Teilchen mit Überlichgeschwindigkeit nicht lol, oh man das ist es zu viel.
Wie schon Leonard Susskind gesagt hat „Only crackpots think that taychons move faster than the speed of light“
Aber warte ich baue kurz ein Tachyonentelefon und sagen meinem Vergangenheits ich das ich den post doch nicht schreiben soll, weil es keinen Sinn hat.
@Florian: Haha, ok gut, wenn das in deinem neuen Buch vorkommt dann musst du wohl auch alle neuen Experimente und Erkenntnisse die man in neuerer Zeit gefunden hat besprechen. Z.B. neue modifikationen der Alcubierre Metrik und Anwendung auf eine höherdimensionale Mannigfaltigkeit und alle Erkenntnisse aus den aktuellen Experimenten von Harold White im NASA Johnson Space Center die auch die Q-Thruster Technologie darauf anwenden die von vier verschiedenen Labors bestätigt wurde, und Lichtgeschwindigkeit wird mit diesen neuen Modellen lokal nicht überschritten und Impuls bleibt auch erhalten. Dazu musst du aber erst mal die Q-Thruster Technologie verstehen an der geforscht wird um zu wissen was die dort versuchen. Das ist nicht mehr wie zu der Zeit wo Alcubierre seine Arbeit geschrieben hat. Viel Spaß, ansonsten wirds halt Quatsch. ;D
Und Teilchen die schneller als Licht sind sind also keine Pseudowissenschaft, aber warp drive schon? So ein quatsch, es ist mit Sicherheit anders rum. Sieht man ja das die Arxiv Version schon unter General Physics ist, das ist der Bereich in den jeder mögliche Kram kommt, hauptsächlich crackpotery. Und Tachyonen bewegen sich nicht schneller als Licht, Tachyonen bedeuten das es keinen stabilen Vakuumzustand gibt. Stell dir einfach eine Potentialfunktion x^2 vor, wenn es Tachyonen geben würde dann wären Potentialfunktionen wie -x^2 möglich dann würde alle möglichen Dinge passieren die keinen Sinn geben. Aber alright, wie gesagt vielleicht baust du dir einfach auch ein tachyonen Telefon und sagst dem Florian in der Vergangenheit bescheid. Schöne Grüße
@Hallodry: Ok. Ich muss ja auch nicht mit dir diskutieren…
Ich hätte eine kurze Frage, die vermutlich etwas naiv ist. Aber wurde bei Supernovae nicht längst beobachtet, dass die Neutrinos gleichzeitig mit den Photonen bei uns ankommen? Ist damit nicht erwiesen, dass Neutrinos masselos sind?
Nee, Nanda, die ExplosionsNeutrinos sind durchaus sogar vor dem ExplosionsLicht hier (Beispiel) — aber nur weil sie früher wegkamen. Das ist bei nem PartyEnde ähnlich, die einen brechen abrupt auf, die anderen verquatschen sich noch…
Ach nun komm, ein paar Stunden fallen bei Lichtjahren noch immer unter „gleichzeitig“. 😉
Is halt die Frage was für Neutrinos damals detektiert wurden. Wiki sagt nix dazu. Laut Artikel sollen ja nur die Elektronneutrinos Tachyonen sein.
Interssante Diskussion
Für mich als physikalisch interessierten und elektrotechnisch grundausgebildeten Laien sind komplexe Zahlen eine Grundrechenmethode, um die wechselstrommäßigen (zeitabhängigen) Vorgänge in Spule und Kondensator zu beschreiben. Wir haben das in der Schule ausgiebig gelernt: die Phasenverschiebung von Stom und Spannung (= die komplexe (zeitabhängige) Darstellung der elektrischen Energie) in Spule, Kondensator, Schwingkreis.
Ich kann mir mit diesem Hintergrund sehr gut vorstellen, daß es im elementaren Bereich durchaus Sinn macht, die Dinge (Masse, Energie … ) komplex zu betrachten.
@Peter Gradauer
Die komplexe Wechselstromrechnung ist ein Beispiel, wo man eine Schaltung komplex berechnen KANN, MUSS es aber nicht. Messen tut man eh nur relle Werte.
Ob das für eine eventuelle imaginäre Masse auch gelten könnte, weiss ich natürlich nicht.
@Frantischek Deshalb frage ich ja. Was detektiert wurde, werden wohl Elektronen-Neutrinos sein. Haben die nun eine geringe Masse, oder keine? – Was deine Aussage bzgl. Tachyonen angeht, hätte ich gerne einen Link. Denn das wirft mein Wissen über den Haufen.
@Nanda:
Link? Lies noch einmal den Artikel unter dem wir gerade posten. Da gehts darum das Elektronneutrinos evtl. Tachyonen mit imaginärer Masse sein könnten…
Die dazu gehörige Arbeit ist auch verlinkt.
@Frantischek: Das habe ich ja auch gelesen und sogar so halb verstanden. Aber es erklärt mir nicht meine Eingangsfrage. Warum kommen denn die Neutrinos nach einer Supernova gleichzeitig mit den Photonen bei uns an? Wenn sie positive oder theoretische negative Masse hätten, müsste es doch einen deutlichen Zeitverzug geben.
Hallo,
@Florian Komplexe Zahlen kommen in Österreich sicher in der Oberstufe relativ ausführlich vor, ich war wie du sehr überrascht, dass das in D nicht der Fall ist.
Bzgl. Wellenfunktion: Die ist natürlich komplex, allerdings ist physikalisch beobachtbar nur das reelle Betragsquadrat. Meiner Meinung sind imaginäre Zahlen, wenn immer sie vorkommen, rechnerische Hilfsmittel, keine physikalische Realität. Imaginäre Hamiltonfunktionen benutzt man um Energiedissipation zu beschreiben, imaginäre Zeit um Temperatur in die Quantenfeldtheorie zu bringen, und so weiter.
Also zu meiner Zeit im MNG in Bayern waren komplexe Zahlen ab 11. Klasse noch vorhanden, siehe
https://www.isb.bayern.de/download/9018/lehrplanm_g9alt.pdf
oder
https://won.mayn.de/lehrplan/M-11.html
Heute scheint das sich geändert zu haben:
https://www.isb-gym8-lehrplan.de/contentserv/3.1.neu/g8.de/index.php?StoryID=26192
@Nanda:
„Warum kommen denn die Neutrinos nach einer Supernova gleichzeitig mit den Photonen bei uns an? „
Wie oben schon @rolak geschrieben hat, kommen die Neutrinos sogar vor den Photonen bei uns an.
Das liegt daran, dass die Photonen mit allerlei Teilchen per EM-WW wechselwirken, die die Supernova erzeugt (das ist bei der Sonne auch nicht anders. Ein Photon, das im innern der Sonne erzeugt wird, braucht deswegen u. U. ein paar Millionen Jahre bis zur Sonnenoberfläche).
Da Neutrinos aber mit praktisch nix wechselwirken, durchdringen sie die von der Supernova erzeugten Wolke einfach so und sind deshalb früher bei uns.
Das hat allerdings mit dem oben im Artikel beschriebenen Thema nichts zu tun, sondern liegt einfach daran, dass Neutrinos nunmal nich elektromagnetisch wechselwirken.
Jetzt klar?
@Nanda:
Ich kann natürlich nur sagen was ich hier und bei Wiki dazu gelesen hab und ich mir dazu (aus)denke. In den populärwissenschaftlichen Büchern die ich gelesen hab wurde das Thema Neutrinos nie richtig ausführlich behandelt bzw. sind die auch schon etwas älter.
1. Erklärungsversuch:
Die Neutrinos oszillieren ja. D.h. sie wechseln zwischen verschiedenen möglichen Zuständen mehr oder weniger spontan und regelmäßig.
Wenn das stimmt und auf die Beobachtung der Supernovaneutrinos zutrifft wäre es mMn möglich das sie auf dem Weg zur Erde nur einen ziemlich kleinen Teil der Zeit Überlichtschnell unterwegs waren. Nämlich immer dann wenn sie als Elektronneutrinos existieren (und vorausgesetzt das Elektronneutrinos wirklich überlichtschnell, also Tachyonen sind).
Das würde wohl nur funktionieren wenn C nur ein kleines bisschen überschritten wird. Wieviel Spielraum da unter Berücksichtigung der bekannten Gründe für den Laufzeitunterschied (Zeit, die die Photonen brauchen um den Kern des kollabierenden Sterns zu verlassen) bleibt, müsste man ausrechnen. Da bin ich aber der Falsche dafür.
2. Erklärungsversuch:
Was ich gerade geschrieben hab ist Blödsinn. Dann könnten entweder die detektierten Supernovaneutrinos keine Elektronneutrinos gewesen sein und deswegen unterlichtschnell unterwegs.
Oder Elektronneutrinos sind einfach keine Tachyonen und die in Florians Artikel besprochene Arbeit ist ein interessantes Gedanken- und Rechenspiel und nicht mehr.
@PDP10 Danke für die ausführliche Antwort, aber nö, klar ist jetzt gar nichts. Was du beschreibst sind normale physikalische Phänomene. Wenn Neutrinos eine Masse hätten, müssten sie _deutlich_ später als das Licht ankommen. Deine Antwort unterstreicht meine Frage eher.
„Wenn Neutrinos eine Masse hätten, müssten sie _deutlich_ später als das Licht ankommen.“
Warum? Die Masse kann winzig klein sein (muss sie auch, sonst hätte man sie schon messen können). Und dann ist auch der Unterschied zu C nicht groß.
Sogar wenn sie eine größere Masse hätten würden sie sich wohl mit annähernd C von der Supernova entfernen. Auch wesentlich schwerere Protonen können ja superrelativistisch unterwegs sein wenn ihnen genug Energie mitgegeben wird. Und auf dem Weg zur Erde werden sie ja nicht gebremst. Entweder sie kommen an oder sie interagieren auf dem Weg mit einem anderen Teilchen und sind weg.
Nebenbei wird die Wahrscheinlichkeit ein Neutrino zu detektieren größer, je höher dessen Energie ist. D.h. (für mich) wir haben eine sehr viel größere Chance die allerschnellsten Neutrinos zu finden. Und selbst von denen nur eine Hand voll.
Es könnte also durchaus sein das da draussen noch viel mehr Neutrinos von der Supernova unterwegs sind die erheblich länger unterwegs sind.
Was sagen die Experten dazu? Kommt mir einleuchtend vor, aber das muss je nix heissen.
@Frantischek:
Wenn etwas jemals schneller als c ist, kann es niemals langsamer als c werden. Die Hürde c gilt auch für Tachyonen, nur eben umgekehrt.
Daher freunde ich mich eher mit deiner Erklärung #2 an. „Elektronneutrinos sind einfach keine Tachyonen“. Ich würde sogar so weit gehen, zu sagen, dass Tachyonen schlichtweg nicht existieren.
Da hast du wohl recht. Aber dieses etwas würde sich ja in dem Fall in ein anderes etwas umwandeln. Und dieses etwas wäre dann mit <C unterwegs.
So hab ich das verstanden und gemeint. Wie weit das wirklich zutrifft… *Achselzuck*
@Frantischek:
Viel zu kompliziert ..
@Nanda:
Es liegt wirklich nur daran, dass die Neutrinos auf dem Weg vom Kern der Supernova zu uns mit nichts wechselwirken.
Die Photonen schon. Sie werden auf dem Weg zu uns immer wieder absorbiert und emmitiert und knallen gegen Teilchen usw. Dh. Die brauchen viel länger um aus der Supernova „rauszukommen“ nachdem sie erzeugt wurden und sind deshalb auch später als die Neutrinos bei uns.
Das ist wirklich alles.
In der Sonne ist das wie gesagt auch so.
Wir können Neutrinos detektieren, die bei den Fusionsprozessen im Kern der Sonne erzeugt werden, und die viel, viel früher bei uns sind, als die Photonen, die auch dabei erzeugt werden – aus den genannten Gründen.
@PDP10:
Das heist ja aber schlussendlich, dass Neutrinos eben nicht schneller oder langsamer als das Licht sind, also eben auch keine Masse haben.
@Frantischek:
Wir sprechen hier von einer Entfernung von Milliarden von Lichtjahren. Wenn Neutrinos nur eine ganz winzige Masse hätten, würde das Monate oder sogar Jahre ausmachen. Nicht Stunden.
„Wenn Neutrinos nur eine ganz winzige Masse hätten, würde das Monate oder sogar Jahre ausmachen.“
Das, und das kann ich auch als Laie sicher sagen, stimmt nicht.
Wenn die Geschwindigkeit nahe genug an C ist wird auch der Laufzeitunterschied minimal sein.
Es ist schon klar das der Unterschied dann winzigst sein müsste.
Ein Jahr hat ca. 8700 Stunden. Wenn die Neutrinos also 1 Milliarde Lichtjahre zurücklegen müsste der Geschwindigkeitsunterschied kleiner als ein Achttausendsiebenhundertmilliardstel sein um einen Laufzeitunterschied von einer Stunde zu ergeben.
Das klingt wahrlich klein. Aber da gibts in der Teilchenphysik kleinere Zahlen mit denen gerechnet wird (und die Rechnungen funktionieren und bringen überprüfbare Ergebnisse).
Protonen im LHC erreichen z.B.etwa 99,999999 % der Lichtgeschwindigkeit. Das wäre nach meiner Kopfrechnung schon 6 oder 7 Nachkommastellen an der benötigten Geschwindigkeit dran. Und Supernovas haben schon viel mehr Bums als der LHC. Und Neutrinos schon viel weniger Masse als Protonen.
Also nicht unbedingt unmöglich, finde ich.
@PDP 10:
„Es liegt wirklich nur daran, dass die Neutrinos auf dem Weg vom Kern der Supernova zu uns mit nichts wechselwirken.“
Naja. Das sagst du, und wohl auch die meisten anderen Leute. Aber offensichtlich gibts mindestens einen Wissenschaftler der sagt das überlichtschnelle (Elektron)Neutrinos nach heutigem Wissensstand noch möglich wären. Ich gehe davon aus das der Herr das durchgerechnet hat. Und wahrscheinlich über den Stand der Forschung besser informiert ist als wir.
Und sollte da was dran sein, dann muss es auch einen Anteil an den Laufzeitunterschieden haben, oder?
Wie groß dieser Anteil ist, und ob er überhaupt vorhanden ist, kann ich natürlich nicht sagen. Aber es geht ja hier auch nicht um konkrete Forschungsergebnisse sondern um eine theoretische Möglichkeit.
Supernovae natürlich, nicht Supernovas…
Was die Sache mit den Supernovae angeht: Das wird im Artikel von Ehrlich am Ende extra erwähnt; mit Abschätzung wie man das Phänomen überprüfen kann. Ich bin aber grad im Stress und kann nicht nachlesen. Vielleicht möchte jemand anderes kurz nachsehen?
Ausserdem glaube ich das hier ein kleines Missverständnis herrscht.
Die Masse eines Teilchens ist wohl nicht direkt proportional zu dessen Geschwindigkeit. Nur zu der Energie die aufgewendet werden muss um das Teilchen zu beschleunigen.
Meiner Meinung nach können Teilchen nahezu beliebig nah an C beschleunigt werden solange die Gesamtenergie des Teilchens eine bestimmte Größe nicht überschreitet ab dem es zu einem mikroskopischen schwarzen Loch werden sollte.
Wie groß diese Energie ist weiss ich allerdings nicht.
Anyone?
Sorry für den Tripplepost…
@Frantischek
du kannst jedes teilchen beliebig nahe an c beschleunigen, wenn du nur genügend energie reinsteckst. die energie ist nach oben nicht beschränkt. ein schwarzes loch kann daraus niemals enstehen. wieso sollte auch plötzlich ein schwarzes loch draus werden, nur weil es sich schenller bewegt?? (geschwindigkeit ist abhängig vom bezugssystem, kann also nicht das kriterium sein ob es zum schwarzen loch wird oder nicht).
„wieso sollte auch plötzlich ein schwarzes loch draus werden, nur weil es sich schenller bewegt??“
Relativistische Massenzunahme?
„relativistische massenzunahme“ hat damit gar nichts zu tun.
eine sache vorweg: genau wegen solchen missverständnissen (und wegen der generellen nutzlosigkeit) wird der begriff einer geschwindkeitsabhängigen „relativistischen masse“ in der physik seit ewigkeiten nicht mehr verwendet (nur in populärwissenschaflticher literatur hält er sich nach wie vor tapfer und unangefochen). wenn irgendwo von „masse“ eines teilchens die rede ist, dann ist das in der physik IMMER die invariante masse (=“ruhemasse“).
also warum kann jetzt durch bewegung kein schwarzes loch aus einem teilchen werden: das erste argument wie man es ganz leicht sehen kann habe ich oben schon erwähnt: geschwindigkeit hängt vom bezugssystem ab. ein teilchen ist in einem bezugssystem in ruhe, in einem anderen bewegt es sich mit fast c. du kannst nicht ein schwarzes loch enstehen lassen, in dem du ein teilchen einfach nur aus einem anderen bezugssystem betrachtest. das würde bedeuten, dass die erde aus sicht der teiclhen der kosmischen strahlung ein schwarzes loch ist, aus unserer sicht aber nicht. das macht keinen sinn.
das missverständnis scheint daher zu kommen, dass du (so wie viele menschen) die „relativisitsche masse“ als quelle für die gravitationswirkung zu nehmen scheints (so wie im alten Newtonschen gravitationsgesetzt, wo die masse die quelle ist). das ist aber leider falsch! das newtonsche gravitationsgesetzt kannst du vergessen, wenn du teilchen nahe der lichtgeschwindigkeit und schwarze löcher betrachten willst, es gitl hier schlicht nicht. was du benötigst ist die allgemeine relativitätstheorie, und hier funktioniert die gravitation gänzlich anders.
der quellterm für die krümmung der raumzeit (welche dann den effekt erzeugt, den wir als gravitation kennen), also das was dir angibt wie und wie stark die raumzeit gekrümmt wird und damit welche gravitationswirkung ein objekt ausübt, ist der sog. energie-impuls-tensor. ohne genau darauf einzugehen, was das ist, sei einfach nur gesagt dass dies sowas wie eine 4 x 4 matrix (also insgesamt 16 komponenten), deren komponenten größen wie energie- und energiestromdichte, impusldichten,….. sind. haben wir ein teilchen in ruhe, so trägt nur die energie (und weil es ja in ruhe ist entspricht dies seiner masse) bei, da es ja jetzt keinen impuls hat und daher die anderen komponenten alle 0 sind. erhöhen wir die masse, so erhöht sich auch die gravitationswirkung, und wenn die masse groß genug ist, dann kann auch ein schwarzes loch enstehen.
nehmen wir jetzt unser teilchen (welches kein schwarzes lcoh ist)und bewegen es, so wird sich natürlich seine energie ebanfalls erhöhen (weil ja jetzt die kinetische energie noch zu ruheenergie dazu kommt). das ist das, was du als „relativistische massenzunahme“ bezeichnet hast (denn die „relativisitsche masse“ ist in wirklichkeit überhaupt nichts anderes als ein anderes wort für gesamtenergie, und daher ist sie auch so nutzlos, denn was bringt mir ein neues wort für eine altbekannte größe?). ABER, im gegensatz zum vorherigen fall, wo wir die (invariante) masse eines teilchens in ruhe (und damit ebenfalls seine energie) immer weiter erhöht haben, hat das teilchen in bewegen jetzt natürlich auch einen impuls! und dadurch tragen jetzt auch (einige) der anderen komponenten im energie-impuls-tensor bei, und die rechnung funktioniert NICHT mehr so einfach wie: höhere energie –> höhere gravitation.
je schneller du ein teilchen bewegst, desto höher wird seine energie UND sein impuls, und im zusammenspiel aller dieser komponenten im quellterm für die raumzeitkrümmung wird dadurch niemals ein schwarzes loch bloß dadurch enstehen, dass du ein teilchen aus einem anderen bezugssystem (= mit einer anderen geschwindigkeit) betrachtest.
PS: und nochmal: das konzept einer relativistische massenzunahme führt immer sehr leicht zu missverständnissen (so müsste man z.B. erst recht wieder zwischen einer „longitudinalen“ und einer „transversalen relativistischen masse“ unterscheiden, aber das vergisst dann auch wieder fast jeder), so dass mein ratschläg wäre, das ganze lieber gleich zu vergessen.
@Frantischek:
Ich weiß nicht, ob ich hier Links posten darf, aber falls doch, erklärt dieses populärwissenschafliche Video ein Bisschen deine Frage, warum denn keine Masse auf c beschleunigt werden kann.
https://www.youtube.com/watch?v=mkiCPMjpysc
Hier sogar noch einfacher und „populärwissenschaftlicher“ 😉
https://www.youtube.com/watch?v=NnMIhxWRGNw
Oha! Danke für die Erklärung. Da würd ich gern auch noch ein bissl weiter nachlesen, zum Verständnis. Kannst du mir was empfehlen?
@Nanda:
Hab deinen Post vorher nicht gesehen, sorry.
Wo hast du von mir die Frage gelesen warum keine Masse auf C beschleunigt werden kann?
@Florian:
Ich lese gerade, kann aber nicht behaupten das ich da durchsteige. Bei englischen Fachausdrücken wirds für mich richtig anstrengend (bin schon froh wenn ich mit meinen Londoner Freunden Call of Duty spielen kann…:D).
Ich kopier den Teil hier rein, ich glaub das das kein Copyrightproblem geben dürfte weil ich die Quelle direkt verlinke usw…
Sollte ich mich irren, einfach löschen.
Wenn das wer übersetzen und für normalsterbliche runter interpolieren kann wäre ich sehr dankbar. Weil der Sch*** gibt mir grad RICHTIG zu denken.
Quelle: https://arxiv.org/pdf/1408.2804v7.pdf
@Florian:
Ich habe das PDF gelesen, muss aber gestehen, dass es meinen Horizont leider deutlich übersteigt. Ich bin eben keine Astophysikerin. 😉
Es ware super klasse, falls das mal jemand für Leute wie mich etwas „herunterdummen“ könnte.
@Frantischek:
Also ich habe es mit deinen Beispielzahlen mal durchgerechnet, aber selbst bei 99,999999% c komme ich bei einer Entfernung von einer Milliarde Lichtjahren auf _deutlich_ mehr als ein paar Stunden Differenz.
@Nanda:
Dann hast du meinen Post falsch verstanden.
Bei den von mir erwähnten 99,999999% kommst du natürlich auf eine erheblich größere Differenz. Das ist ja nur die Geschwindigkeit von Protonen in einem menschengemachten Beschleuniger.
Ich hab ja auch nur geschrieben das wir damit bis auf 6-7 Nachkommastellen an der benötigten Geschwindigkeit sind (aber eben im Labor, und nicht in einer SN).
Und das Protonen viel schwerer als Neutrinos sind. Und das Supernovae viel mehr Energie als ein Teilchenbeschleuniger bereitstellen.
Und ich es deshalb nicht für unwahrscheinlich halte das ein Teilchen das evtl. nur eine Milliardstel, Billionstel oder noch weniger als die Protonmasse besitzt durch diese extrem viel höhere Energie auf die erforderliche Geschwindigkeit beschleunigt werden kann.
Oh, und nochmal @Frantischek:
Ich habe deinen Post ebenfalls erst jetzt gesehen und bitte ebenso für die Mehrfachposts um Vergebung. 😉
Ich hatte einen deiner Posts eben so verstanden. Besonders den Teilsatz: „Meiner Meinung nach können Teilchen nahezu beliebig nah an C beschleunigt werden“
Und da fielen mir eben diese beiden Videos ein, die ich sehr anschaulich finde.
@Nanda
Die einzigen Neutrinos, die bisher von einer Supernova nachgewiesen wurden, sind die von der Supernova 1987a, und die war „nur“ 168000 Lichtjahre entfernt (siehe zitierten Text in #70). Es wurden, soweit ich mich erinnere, gerade mal 13 Neutrinos nachgewiesen. Diese erschienen ein paar Stunden vor dem Aufleuchten der Explosion.
Wie PDP10 bereits erklärt hat, werden Neutrinos beim Kernkollaps nicht aufgehalten, sie entstehen sofort in Bruchteilen von Sekunden, während der Kern des Sterns zu einem Neutronenstern kollabiert, wobei die Protonen und Elektronen sich per inversem Beta-Zerfall zu Neutronen und Neutrinos wandeln. Und sie verlassen sofort den Stern (tatsäschlich sind es so viele, dass einige von ihnen über die schwache Wechselwirkung einen nicht unerheblichen Druck auf das Gas ausüben, das scheint entscheidend für die Explosion zu sein, wie ich kürzlich las).
Das Licht der Explosion entsteht durch Kernfusion entlang der Stoßfront, die durch den Stern läuft, und später vor allem durch radioaktiven Zerfall der entstandenen Isotope (deswegen leuchten sie wochenlang weiter). Die Stoßftront frisst sich von innen nach außen durch den Stern und es dauert ein paar Stunden, bis sie die Oberfläche erreicht (deutlich schneller, als Photonen aus dem Zentrum der Sonne diese verlassen können, aber eben langsamer als die Neutrinos, die sofort mit ungefähr Lichtgeschwindigkeit entkommen).
Neutrinos müssen eine kleine Ruhemasse haben (imaginär oder real), denn sie oszillieren nachgewiesenermaßen zwischen ihren drei Flavours (zumindestens habe ich dies als Begründung für ihre Ruhemasse gelesen; ich nehme an, das liegt ganz einfach daran, dass eine solche Oszillaiton Zeit benötigt und ein lichtschnelles Teilchen bei unendlicher Zeitdilatation keine definierte Eigenzeit hat).
Wegen dieser Oszillationen würde es mich übrigens wundern, wenn manche Neutrinoflavours (wie oben irgendwo spekuliert wurde) imaginäre und andere reelle Masse hätten, wenn schon, dann alle die gleiche Art Masse, sonst würden sie ja irgendwie die Lichtgeschwindigkeit über- und unterschreiten können.
@Nanda
Bei großer Entfernung ist zwar der Laufzeitunterschied groß, aber das Signal wird sehr schwach
Das Problem bei Quellen in großer Entfernung ist, das der Fluß mit 1/r² läuft und Neutrinos (vorallem wenn sie wenig Energie haben) schlecht nachweisbar sind. Bei SN 1987A hat man 24 Neutrinos gesehen, und das war in 170.000 Lichtjahren Abstand. Bei 10-fachen Abstand (grob eine Million Lichtjahre) sind nur noch 2 bis 3 Neutrinos zu erwarten. Bei einer Milliarde als Abstand bliebe davon nur noch ein millionstel übrig.
Das würde also im Untergrund verschwinden und würde viel bessere (, größere und teurere) Detektoren benötigen. Zum Beispiel bräuchte man 5.000.000.000 Tonnen Wasser, um etwa so viele Neutrinos wie bei SN1987A zu detektieren.
@Alderamin:
vielen Dank für deine ausführliche Antwort. Ich fand sie sehr interessant und spannend. Aber beschreibt dein Ausgangsabsatz nicht exakt meine Frage?
@JaJoHa:
Ich weiß nicht genug über das Thema, um dir zu widersprechen. Ich habe nur mal vor Jahren in einem wissenschaftlichen Artikel gelesen, dass Neutrinos von Supernovae grob gleichzeitig mit den Photonen bei uns eintreffen. Das Thema kam in der „Populärwissenschaft“ wieder auf, als herauskam, dass sich CERN geirrt hat. Zugegeben, das mit der Entfernung hatte ich von Wikipedia, und da habe ich nach Supernova und nicht nach Neutrino gesucht. Aber ich bin doch auch nur ein Mensch. 😉 Wenn ich dich richtig verstehe, geht unsere Chance, die Wahrheit bei unseren aktuellen Möglichkeiten herauszufinden, also gegen Null und es bleibt eine rein mathematische Möglichkeit. Also eben einfach nicht ausgeschlossen. Oder vertsehe ich dich gerade komplett falsch?
@Nanda
Worauf ich hinaus wollte ist folgendes: Man muss Glück haben, das die Supernova nahe genug ist, das man die Neutrinos überhaupt messen kann. Ist sie zu weit weg, dann kann man die Neutrinos nicht vernünftig messen. Ist die Messstrecke zu kurz, dann wird die Messung schwierig weil die Unterschiede in der Flugzeit klein sind.
@Nanda
Die Frage war, ob die Messungen der Neutrinolaufzeit von Supernovae nicht belegen würden, dass die Neutrinomasse 0 ist, und die Antwort darauf ist nein, denn das optische Aufleuchten ist so stark verzögert, dass man daran keine gleiche Laufzeit festmachen kann.
Die Frage an JaJoHa, ob die Chance gleich Null sei, die Neutrinomasse herauszufinden, ist ebenfalls mit nein zu beantworten, denn der von frantischek in #70 zitierte Text weist eine Möglichkeit auf, nämlich danach zu suchen, ob die Laufzeit der Neutrinos von ihrer Energie abhängig ist – ob kurzperiodische Schwankungen in der Erzeugungsrate der Neutrinos durch verschiedene Laufzeiten von Neutrinos verschiedener Energie verschmiert würden (dazu müsste man aber eine ganze Menge von ihnen empfangen, und nahe Supernovae wie 1987A sind vielleicht alle 50-100 Jahre zu erwarten). Außerdem besteht die Möglichkeit, mit Experimenten wie KATRIN nach der Masse zu suchen. Dabei werden Beta-Zerfälle beobachtet, bei denen Elektronen und zugehörige Elektron-Antineutrinos entstehen, auf die sich die Gesamtenergie zufällig verteilt. Die allerschnellsten Elektronen werden also die maximale Energie des Zerfalls minus der Neutrinoruhmasse mit sich führen. KATRIN versucht, die Energie dieser Elektronen möglichst genau zu messen. Aus der Differenz zur Energie des Beta-Zerfalls folgt die Neutrinomasse für das Elektron-Antineutrino.
@Frantischek:
Was den von dir hier rein kopierten Ausschnitt des Papers angeht (nein, bin noch nicht dazu gekommen das ganze Paper zu lesen):
Da ist nur die Rede davon, wie man den gemessenen Neutrino-„Puls“ auswerten müsste um seine Hypothese zu überprüfen.
Er beschreibt einfach quantitativ, was man rauskriegen müsste wenn seine Hypothese richtig wäre und was, wenn sie widerlegt würde.
Nochmal:
Mit der Frage, warum die Neutrinos die von einer Supernova erzeugt werden vor den Photonen ankommen hat das nix zu tun.
Die Zeitlichen Unterschiede die er in dem Absatz erwähnt wären auch einfach zu klein.
Siehe @Alderamins, @JaJoHas und meine Posts für die Erklärung dafür.
Jopp!
In der Entfernung in der SN1987a war auf jeden Fall. Das hätte mir aber auch auffallen können. Ich hab die „milliarden Lichtjahre“ einfach übernommen und nicht weiter drüber nachgedacht.
Bei so langen Laufzeiten könnte doch ein beobachtbarer Unterschied auftreten, oder?
@Alderamin: Ok, also sollten wir uns darauf einigen, dass wir alle mal einfach abwarten sollen? So verstehe ich deinen Post zumindest und habe auch kein Problem damit. – Ich möchte die Dinge einfach nur verstehen, aber wenn die klügsten Köpfe sagen: „Das verstehen wir selbst noch nicht, aber wir sind dran!“, dann ist das für mich ausreichend.- Zumindest habe ich deinen Punkt verstanden. 😉
@Frantischek:
Ich verstehe auch nicht so ganz, warum er 1987a explizit erwähnt.
Wie gesagt, ich hatte noch keine Zeit das Paper zu lesen.
Vielleicht liegen ihm die Originaldaten nicht vor oder er benutzt das als Beispiel um eine Messgleichung / Vorschrift zu beschreiben.
Wie gesagt, ich habe das komplette Paper nicht gelesen, deshalb fehlt mir da der Kontext …
@Nanda
So ungefähr. Lange müssen wir ja vielleicht gar nicht mehr warten, wenn KATRIN ein Ergebnis liefert (zumindest wird es eine neue, engere Obergrenze liefern).
@frantischek
Die Empfindlichkeit unserer Neutrinodetektoren ist zu gering, um damit Supernovae in vielen Millionen oder gar Milliarden Lichtjahren Entfernung nachzuweisen, wie JaJoHa schon schrieb. Es muss schon ein Puls von ihnen aus der gleichen Richtung kommen, um sie von sporadischen Ereignissen zu unterscheiden (und ihr Spektrum oder zeitliches Verhalten zu analysieren), und das klappt nur für nahe Supernovae, die unglücklicherweise selten sind.
Prinzipiell wäre ja ein kurzer GRB viel spannender, weil zeitlich sehr beschränkt, denn da verschmelzen höchstwahrscheinlich zwei Neutronensterne zu einem Schwarzen Loch, was ziemlich flott vonstatten geht. Da wäre das „optische“ Signal (eben die Gammastrahlung) weit weniger verzögert als bei einer gewöhnlichen Supernova. Ich bin mir aber nicht sicher, ob dabei überhaupt viele Neutrinos frei werden.
@all
Was ich mich gerade frage:
Neutrinos treten ja so gut wie nicht mit normaler Materie in Wechselwirkung.
Wenn Neutrinos dunkle Materie sind, warum können sie dann bei Zerfallsprozessen von normaler Materie entstehen?
Lg H.
Da ich selbst eine Theorie über Tachyonen aufgestellt habe, interessiere ich mich sehr an der Arbeit von Ehrlich.
Aber bevor ich weiter darauf eingehen möchte, eine kurze Frage. Es fiel folgender Satz:
„…Protonen die sehr hohe Energien haben zerfallen zu Neutronen und Neutrinos…“
Ist es nicht exakt umgekehrt und stammt dieser Satz wirklich von Ehrlich?
MfG
WL01
Mit welcher Genauigkeit hat man eigentlich die Geschwindigkeit von Neutrinos durch direkte Messung ermittelt (nachdem man die berühmt-berüchtigten Kabel richtig verbunden hatte)?
@Higgs- Teilchen
Über die schwache Wechselwirkung, die beim Beta-Zerfall eine Rolle spielt. Dunkle Materie wechselwirkt nur nicht elektromagnetisch, also mit Licht, aber kann sich durchaus per Gravitation und schwacher Wechselwirkung bemerkbar machen. Ob die gesuchte kalte Dunkle Materie schwach wechselwirkt, ist aber auch noch nicht ausgemacht.
@Felix
„Gemäß der speziellen Relativitätstheorie ist die Neutrinogeschwindigkeit geringfügig langsamer als Lichtgeschwindigkeit. Bisherige Messungen ergeben eine obere Grenze für Abweichungen von 10^-9, also ungefähr ein Milliardstel der Lichtgeschwindigkeit. Das ist im Rahmen der Messgenauigkeit in Übereinstimmung mit der Vorhersage der Relativitätstheorie.“
Außerdem war es nicht der Kabelfehler allein, sondern eine zusätzliche Fehlerquelle, angeblich ein Ozillator.
Steht hier:
https://de.wikipedia.org/wiki/Messungen_der_Neutrinogeschwindigkeit
MfG
WL01
@Alderamin, Higgs-Teilchen
Wenn Neutrinos „Dunkle Materie“ wären, dann würde sich natürlich eine gravitative WW (positive Materie und positive Materie ziehen einander an) ergeben.
Aber gilt diese Vorgabe auch wirklich für Tachyonen?
Wenn man beispielsweise zwei „Komplexe Zahlen“ (mit reellen und imaginären Inhalten) miteinander multipliziert ergibt sich als Ergebnis eine negative reelle Zahl und eine positive imaginäre Zahl.
Müsste man dann nicht die Wirkung von Tachyonen eher mit „Dunkler Energie“ gleichsetzen (positive Materie stößt negative Materie ab)?
MfG
WL01
@WL01
$latex (1-i)^2=-2i$
Hier(resp. Ehrlich) ist doch die Rede von imaginärer Masse (für Tachyonen). Und dem Energie-Impuls-Tensor ist das soweit egal (siehe E= im Blog-Artikel) – „negative Masse“ xor „negative Wurzel“ würde „negative Energie“ liefern. Über $latex e^{i\phi}$ ist imaginäre Masse eher als eine „phasengedrehte“ Masse interpretierbar (wobei keineswegs klar ist was da unter „Phasendrehung der Masse“ zu verstehen wäre; der DeBroglie-Welle ist’s eher egal… – …eine Art „Feldkoppelung“(ähnlich B und E) funktioniert ja wohl auch nicht richtig wegen den impliziten unterschiedlichen Geschwindigkeiten…)
@all
Moment! Es gibt drei unterschiedliche Neutrinos. Und sie können sich in einander umwandeln. Aber wieso taucht dann nur das Elektron-Neutrino im Standart-Modell auf???
@Hits-Teilchen
Tut es doch nicht. Guckst Du hier (Grafik rechts)
@Alderamin
Ach ja, richtig. Danke.
Hatte spontan nur an die erste Teilchenfamilie gedacht. 🙂
@Alderamin
Nur verstehe ich dann nicht, wie sich die ineinander umwandeln können. Die haben doch alle unterschiedliche Energien. Wie funktioniert das?
@Higgs-Teilchen
U.U. gibt’s ja auch noch Sterile Neutrinos.
@Higgs-Teilchen
So richtig habe ich das auch nicht verstanden. Neulich hat Reggid versucht, es mir zu erklären, siehe ab hier und folgende.
@Higgs-Teilchen
Zur Oszillation PMNS-Matrix(ff)
@Alderamin
Okay, danke. Hilft mir schon mal. 😉
Ist auch irgendwie beruhigend zu wissen, dass ich nicht der Einzige bin der bei Neutrinos nicht mitkommt. 😉
Ich werde irgendwann 2015 mal nen Neutrino-Experten auftreiben und das Thema ausführlich behandeln…
Imaginäre Massen, Reisen rückwärts in der Zeit, … Was kommt als nächstes, ein sprechendes weißes Kaninchen?
@Alderamin @Higgs-Teilchen
Neutrino-Oszillation ist kein Hexenwerk.
Man muss allerdings die Sache mit der quantenmechanischen Superposition (also dem Überlagerungszustand) einigermaßen verinnerlicht haben.
Reggid hat drüben eigentlich schon alles beantwortet und dem „Neutrino oscillation“-Wikipediaeintrag kann ich auch nicht wirklich viel hinzufügen.
Ich bemühe mich aber einfach mal, das etwas laienfreundlicher aufzuarbeiten.
Neutrinos können nur dann vernichtet (also beispielsweise beobachtet) oder erzeugt werden, wenn gleichzeitig auch ein geladenes Lepton (also Elektron, Myon bzw. Tau) oder Anti-Lepton erzeugt oder vernichtet wird. Dieses Neutrino wird dann nach dem zugehörigen Lepton benannt.
Der Flavour (hier der Lepton-Flavour) ist also einfach nur eine weitere Quantenzahl der Quantenmechanik. Andere Quantenzahlen sind etwa die Ladung, der Spin, die Impulsquantenzahl, die Baryonenzahl, …
(Tatsächlich ist nicht völlig klar, ob die Leptonenzahl erhalten bleibt. Das spielt aber eigentlich nur für das frühe Universum eine Rolle (dort aber wahrscheinlich eine entscheidende), im „Alltag“ kann man davon ausgehen, beobachtet wurde eine Abweichung bisher noch nicht.)
Das Neue an der Quantenmechanik ist bekanntlich, dass messbare Größen (Observablen) im Allgemeinen in einem quantenmechanischen Zustand keinen wohlbestimmten Wert besitzen. Das bedeutet, dass man als Ergebnis einer Messung nur Wahrscheinlichkeiten für die verschiedenen möglichen Messergebnisse vorhersagen kann.
Es gibt allerdings zu jeder Observablen einen Satz von speziellen Zuständen, bei denen das Ergebnis einer Messung nicht streuen kann, sondern eindeutig feststeht. Ein solcher Zustand heißt Eigenzustand. Das zugehörige Messergebnis heißt Eigenwert dieses Eigenzustandes.
Befindet sich das System nicht in einem Eigenzustand, spricht man dagegen von einem Superpositions-Zustand (oder Überlagerungszustand). Solch ein allgemeiner Zustand ist immer eine Superposition (also eine Überlagerung) aller möglichen Eigenzustände.
Hier sind also verschiedene Messergebnisse möglich.
Bei einer Messung misst man allerdings immer einen Eigenwert. Die Wahrscheinlichkeit, einen bestimmten Eigenwert zu messen, ist das Betragsquadrat des Faktors, mit dem der betreffende Eigenzustand in dieser Überlagerung vorkommt.
(Diesen Anteil eines bestimmten Eigenzustandes nennt man Wahrscheinlichkeitsamplitude. Das Betragsquadrat dieser Wahrscheinlichkeitsamplitude gibt an, mit welcher Wahrscheinlichkeit man den zu diesem Eigenzustand gehörenden Eigenwert misst.)
Das quantenmechanische System befindet sich nach der Messung in dem Eigenzustand, der zu diesem gemessenen Eigenwert gehört.
(Das nennt man Zustandsreduktion, in der Kopenhagener Interpretation interpretiert man das also den berühmten „Kollaps der Wellenfunktion“ bei einer Messung.)
So, das war ein kurzer Exkurs zu den Grundlagen der Quantenmechanik.
J
etzt aber endlich zu den Neutrinos:
Neutrinos werden nur bei elektroschwachen Wechselwirkungen erzeugt. So eine Wechselwirkung entspricht einer Messung, nach der Erzeugung befindet sich das Neutrino also in einem der drei möglichen Wechselwirkungs-Eigenzuständen. Zu diesen Eigenzuständen gehört jeweils eine Flavour-Quantenzahl.
Einfacher ausgedrückt:
Unmittelbar nach der Erzeugung ist ein Neutrino eindeutig ein Elektron-Neutrino. Oder eben ein Myon-Neutrino. Oder ein Tau-Neutrino. Je nachdem, welches Lepton bei der Erzeugung erzeugt oder vernichtet wurde.
Das besondere bei Neutrinos ist jetzt:
Jeder Flavour-Eigenzustand ist eine Superposition von drei Masse-Eigenzustände.
Es gilt also:
F1 = a11*M1 + a12*M2 + a13*M3
F2 = a21*M1 + a22*M2 + a23*M3
F3 = a31*M1 + a32*M2 + a33*M3 {*}
F1, F2, F3 sind die drei Flavour-Eigenzustände
M1, M2, M3 sind die drei Masse-Eigenzustände
Die aii sind die Faktoren, mit denen die Masse-Eigenzustände in der Superposition vorkommen.
Umgekehrt ist jeder Masse-Eigenzustand eine Superposition der drei Flavour-Eigenzustände.
M1 = b11*F1 + b12*F2 + b13*F3
M2 = b21*F1 + b22*F2 + b23*F3
M3 = b31*F1 + b32*F2 + b33*F3 {**}
Dabei sind die bii die komplexe Konjugation der aii.
(Aus aii = c + i*d folgt also bii = c – i*d. )
Diese Faktoren sind letztlich einfach komplexe Zahlen, die man experimentell bestimmen muss.
Die aii bilden zusammen eine Matrix, die Neutrino-Mischungs-Matrix.
Direkt nach der Erzeugung, also zum Zeitpunkt t=0, befindet sich ein Neutrino wie gesagt in einem Flavour-Eigenzustand, etwa F1(0) für ein Elektron-Neutrino.
Die Zeitentwicklung dieses Zustandes hängt jetzt nur von der Gesamtenergie E des Neutrinos ab. Sowie von den drei Eigenmassen mi zu den Eigenmassenzuständen Mi.
Die Masseeigenzustände entwickeln sich also zeitlich:
M1(t) = f (E, m1, t) * M1(0)
M2(t) = f (E, m2, t) * M2(0)
M3(t) = f (E, m3, t) * M3(0) {***}
f ist immer dieselbe Funktion, die wie gesagt von der Zeit, der Gesamtenergie E und den Eigenmassen mi abhängt.
Jetzt setzt man {***} in {*} ein und so Erhaltene dann in {**}.
Berücksichtigt man zusätzlich, dass man die Funktion f ohne Einschränkung der Allgemeinheit als ebene Welle annehmen kann, erhält man letztlich für den Flavour-Zustand:
F(t) = A(t) * F1(0) + B(t) * F2(0) + C(t) * F3(0)
Wie oben besprochen ist die Wahrscheinlichkeit, das Neutrino mit dem Flavour F1, F2 oder F3 zu messen (also Elektron-, Myon- oder Tau-Neutrino zu detektieren das Betragsquadrat der Wahrscheinlichkeitsamplituden, also in dieser vereinfachten Darstellung die Betragsquadrate von A, B und C und damit des Faktors, mit dem die Zustände F1, F2 und F3 in den Superpositions-Flavour-Zustand eingehen.
Da die Funktion f(t) eine ebene Welle ist, oszilliert das Ganze mit einer bestimmten Periode und besitzt eine Phase. Ein Neutrino, das als Elektron-Neutrino erzeugt wurde, befindet sich nach einer Periode also wieder im Elektron-Neutrino-Eigenzustand und wird dann wieder als solches gemessen.
In den Zeiten dazwischen kann es allerdings auch mit einer gewissen (zeitabhängigen) Wahrscheinlichkeit als Neutrino mit einem der anderen beiden Flavours detektiert werden.
Im Wikipedia-Artikel findet man unter „Three neutrino probabilities“ schöne Schaubilder. Dort kann man die Wahrscheinlichkeiten für die Detektion der verschiedenen Flavour einfach ablesen.
Zu beachten ist dabei, dass auf der x-Achse als Einheit Strecke pro Energie gewählt wurde.
Die Zeitabhängigkeit lässt sich im Fall ebener Wellen problemlos in eine Wegabhängigkeit umrechnen. Die Wellenlänge der Oszillation ist dabei proportional zur Neutrino-Energie, und zwar ungefähr 35000 Kilometer pro Gigaeelektronenvolt.
Das war jetzt länger als geplant. Hoffentlich war es irgendwie verständlich. Das Ganze ist etwas flapsig und ungenau, ich wollte es aber absichtlich einfach halten. Hoffentlich haben sich dadurch keine gravierenden Fehler eingeschlichen.
Wenn etwas unklar ist, bitte nachfragen.
Das hat mit der Neutrino-Oszillation eigentlich nichts zu tun. Wenn die Neutrino-Mischungs-Matrix nicht unitär wäre, dann würde es solche Teilchen geben. Das ist aber rein hypothetisch.
@Realistischer
Kennst du den Unterschied zwischen Theorie und Fantasie ?
@Niels
Wow, danke. Das Konzept, dass Massen Eigenzustände haben können, muss man allerdings erst mal verdauen, das ist ziemlich wierd. Das ist meine eigentliches Verständnisproblem. Laut Reggid sind die Massen anscheinend ähnlich, zwischen denen da oszilliert wird und somit im Rahmen der Unschärferelation, allerdings gibt der Wiki-Artikel zum Standardmodell extrem unterschiedliche Massenobergrenzen an (von 2 eV beim Elekron-Neutrino bis zu 18.2 MeV beim Tau-Neutrino), das verwirrt. Liegt aber wohl einfach an der Messgenauigkeit der entsprechenden Reaktion. Taus sind ja eher seltener anzutreffen als Elektronen, also wird es auch weniger Beta-Zerfälle mit Tau-Beteiligung geben als solche mit Elektronen, was die Statistik hinsichtlich der Tau-Neutrinos limitiert. Nehme ich an.
@maunz:
Nun, jedenfalls kennt @Realistischer Harvey nicht.
„Man kann auf zwei Wegen gut durch das Leben kommen, entweder man ist sehr schlau oder sehr freundlich. Früher war ich sehr schlau, nun bin ich sehr freundlich.“
😉
@Alderamin
Das sind aber eben nur die Grenzen. Und die ist für das Elektronneutrino am kleinsten, weil das am besten messbar ist, beispielsweise mit Tritium. Da zerfällt ein Neutron praktisch in Ruhe und du bremst das Elektron mit einem Gegenfeld ab.
Die Myonneutrinos könntest du in den Zerfällen von Mesonen (vermutlich am besten in geladenen Pionen) messen, aber da musst du den Impuls vom Meson und dem enstehenden Myon messen, um an die invariante Masse vom Neutrino zu kommen. Und das ist eben viel ungenauer. Und beim Tau wird das noch schlimmer, weil das keinen vernünftigen Track hinterlässt (kommt nur einge 100 µm weit), sondern aus seinen Zerfallsprodukten rekonstruiert werden muss. Die üblicherweise Hadronen und Neutrinos beinhalten.
Das wird also sehr kompliziert und schwierig zu messen.
@Alderamin
Tatsächlich ist das aber sozusagen der Normalfall.
Schließlich mischen auch die Quarks, nämlich über die sogenannte CKM Matrix.
Bei den Quarks passen die Flavour-Zustände allerdings (zufällig?) besser zu den Massenzuständen, deswegen fällt das nicht so stark auf.
Dazu gibt es hier ein schönes Schaubild:
https://universe-review.ca/I15-24-neutrino5.jpg
„Echt elementar“ sind ja die Quarks, die 3 geladenen Leptonen (Elektron, …), die drei ungeladenen Leptonen (Elektron-Neutrino, ) und die Austauschteilchen (Photon, Gluon, W+, W- und Z0) sowie das Higgs.
Insgesamt sind das 61 Elementarteilchen (Quarks und Leptonen zählen wegen der Antiteilchen doppelt, Quarks zusätzlich wegen der verschiedenen Farbladung doppelt.)
Nach Adam Riese liegt diese Fall also bei 42 der 61 Elementarteilchen vor. 😉
(Übrigens sind auch das Photon, das W+ und das W- sowie das Z0 Superpositionszustände, nämlich aus den nicht beobachtbaren Teilchen W0, W1, W2 und B0.)
An der ganzen Chose ist letztlich der Higgs-Mechanismus schuld, durch ihn werden Oszillationen zu einer grundlegenden Eigenschaft der (elektro)schwachen Wechselwirkung.
Deswegen oszillieren auch mehrere Hadronen, das bekannteste Beispiel dürfte das K0-Meson (also das neutrale Kaon) sein.
https://de.wikipedia.org/wiki/Kaon#Mischung_der_neutralen_Kaonen
Ich befürchte, da hast du etwas nicht völlig verstanden.
Die Unschärferelation wird hier nicht benötigt. Die Energie des betrachteten Neutrinos bleibt die ganze Zeit gleich.
(Bei Quarks wird ja auch zwischen völlig unterschiedlichen Massen oszilliert.)
Oszillation ist vielleicht ein irreführender Begriff.
Ein Neutrino (bzw. ein Quark) ist wie gesagt ein Überlagerungszustand. Das ist eine intrinsische Eigenschaft (der Wellenfunktion) dieses Teilchens.
Die Neutrino-Oszillation erfordert also keinen Zerfall, keine virtuellen Teilchen und keine Wechselwirkung. Während des Fluges wandelt sich ein Neutrino nicht tatsächlich einmal in ein Tau-Neutrino, dann in ein Elektron-Neutrino usw. um.
Es bleibt einfach solange in seinem intrinsischen Superpositionszustand, bis es durch eine Messung auf einen Flavour-Eigenzustand festgelegt wird. Welchen Flavour-Eigenzustand es dabei annimmt, ist zufällig und kann nicht vorhergesagt werden. (Außer es hat wie im vorherigen Beitrag dargelegt gerade exakt eine Periode seit seiner Erzeugung hinter sich.)
Nach der Messung geht es wieder in den Überlagerungszustand über.
Das Konzept der Superposition ist hier absolut entscheidend. Deswegen habe ich das längere Vorwort geschrieben, in dem ich noch einmal kurz Eigenzustand, Eigenwert usw. vorgestellt habe.
Na ja, vermutlich ist dir das völlig klar und ich habe die kurze Bemerkung mit der Unschärfe total überinterpretiert.
In diesem Fall nichts für ungut, vielleicht nützt es ja einem anderen Mitleser. 😉
@Zhar @Alderamin @Bjoern
Die Sache mit der Tscherenkow-Strahlung bei Neutrinos hat mich auch interessiert, deswegen habe ich mal ein bisschen nachgeforscht und folgendes gefunden:
https://arxiv.org/pdf/hep-ph/0209264v2.pdf
In einem Buch habe ich noch etwas über i>neutrino vacuum Cerenkov radiation via the non-local charge structure of the neutrino für überlichtschnelle Neutrinos gefunden.
Und in der Wikipedia findet man
https://en.wikipedia.org/wiki/Modern_searches_for_Lorentz_violation
Ehrlich gesagt hab ich aber noch nie etwas von der „charge structure“ von Neutrinos gehört, kann mir darunter auch nichts vorstellen und habe auf die Schnelle auch keine sinnvollen Quellen dazu finden können.
Über Aufklärung würde ich mich freuen.
Allgemein ist der Witz bei überlichtschnellen Neutrinos wohl, dass dann auch Prozesse möglich werden, die sonst für Neutrinos im Vakuum kinematisch verboten sind.
Die weitere Möglichkeiten sind dann anscheinend neutrino splitting (ν → ννν¯) und neutrino pair production bremsstrahlung (ν → ν e+ e−).
@maunz, PDP10
Die Praxis der Theoriebildung zeigt: wenn die Ergenbisse verwirrend kompliziert sind, hat man meisst einen Fehler gemacht. Warum seid ihr nicht so freundlich und nehmt das zur Kenntnis? Ich weis, der Statusdünkel verbietet es, aber dann lasst wenigstens die Freundlichkeit aus dem Spiel.
„charge structure“ also Landungsstruktur
Würde natürlich der neutralen Ladung von Neutrinos widersprechen.
???Könnte aber dem Formalismus der Antiteilchen geschuldet sein, dass es also von Neutrinos auch Antineutrinos gibt.???
???Und unter Ladung versteht man aber offensichtlich nicht nur „elektrische Ladung“ sondern auch „Farbladung“!???
@Niels
Wenn’s ein Vertipper wäre und „Neutrons“ gemeint war, dann hätte ich unter Teilchen mit „charge structure“ solche verstanden, die aus geladenen Bestandteilen zusammengesetzt sind. Denn wenn ein Neutron aus drei elektrisch geladenen Quarks besteht, dann sollte jedes von denen doch Tscherenkov-Strahlung aussenden können. So wie’s da steht kann ich mir allerdings auch keinen Reim darauf machen.
@Niels
Der Hinweis auf sterile Neutrinos bezog sich i.w. auf „drei unterschiedliche Neutrinos“. Andererseits ist ja die Unitarität der 3×3 Mischungs-Matrix auch nur eine ( wenn auch nicht völlig unbegründete) Modellannahme. Der kleine zusätzliche „Mischungswinkel“ bei 3+1 (oder gar 1+3+1) Modellierungen rückt die 3×3-Mischung ja stets in die Nähe einer unitären Matrix. Gibt es da etwas aktuelleres als → https://arxiv.org/pdf/1412.7806v1.pdf ?
Zu „charge structure“ fand ich mal dies:
https://kenkyo.eng.kyushu-u.ac.jp/memoirs-eng/bulletin/68/1/paper6.pdf
@Alderamin
Hast du meinen Beitrag #107 schon gesehen?
Der hing bis gerade noch im Spam-Filter.
—-
Ich vermute, es hat irgend etwas mit dem non-local zu tun.
Das Buch spricht ja von einer „non-local charge structure of the neutrino“.
Mir ist aber völlig unklar, was eine Ladung nichtlokal sein könnte.
Dazu habe ich bei Amzon ein Buch gefunden (Nichtlokale Ladungen in der Quantenfeldtheorie) sowie eine kurze Bemerkung auf der Seite der Uni Göttingen:
Wie gesagt, davon habe ich aber noch nie etwas gehört.
Mir kommt es eher so vor, als wäre eine (nichtlokale?) Ladungsstruktur von Neutrinos hypothetisch möglich und nicht etwa eine erwiesene Tatsache (wie es die Zitate meiner Ansicht nach implizieren).
Allerdings rate ich dabei eigentlich völlig ins Blaue, davon hab ich absolut keine Ahnung.
Diesen Satz habe ich in einem entsprechenden Paper gefunden:
„Our study of elastic scattering of electrons and their neutrinos on a spinless nucleus shows clearly that if the neutrino is the four – component particle (ν = νD = νe) having a Dirac mass mνD , it must possess both normal
and anomalous electric charges.“
Link:
https://arxiv.org/pdf/physics/0305008.pdf
Tatsache, oder nur These?
@Realistischer,@maunz,@DPD10,@michselbst
. . . .. wunderbar: hPantasie-hTeorie-Oszillation: von Elwood-flavour / Harvey-flavour und Gast-flavour in der Lieblings-GAST-stätte . . . ..
Wichtig die Oszillation als das Wollen des Elwood-flavour, sich selbst und dem Gast- & Harvey-flavours einen Schnaps aus zu geben, zu verstehen. Unsere 3 Flavours bilden eine kleine Kneipe innerhalb der Lieblings-GAST-stätte, denn Elwood erscheint einmal als Flavor-Wirt (Kneipe) und andererseits ist er selber Gast-flavour in der Lieblings-GAST-stätte. Hier wechselwirken beide wie zwei Quantenzustände, wo ein Flavour gemessen werden soll, dabei aber zwei QZ reduziert werden . . . ..
In der hPantasie-hTeorie-Oszillation steht eine Messung für eine Entscheidungen, die Elwood im Sinne des darstellens seines materiellen und imaginären Eigentums trifft.
Entscheidung (Obversable) und m.-imag. Eigentum stellen eine Messung im Sinne von Quantenverschränkung dar . . . ..
. . . .. das soll an „quantuition“ erst mal reichen . . . .. ist ein grosser Spass – der das macht . . . ..
– danke für die Inspiration . . . ..
@Niels
„Ein Neutrino (bzw. ein Quark) ist wie gesagt ein Überlagerungszustand. Das ist eine intrinsische Eigenschaft (der Wellenfunktion) dieses Teilchens.“
Okay, danke. Damit ist mir schon sehr viel geholfen.
@Niels #107
Ok, also sagst Du mir also, ein und dasselbe Teilchen kann bei einer Messung, je nachdem, wie die Wellenfunktion gerade zufällig kollabiert, mal 0,2 eV und mal 18,2 MeV Masse haben? Oder bei den u/c/t Quarks mal 2,3 MeV, mal 173,07 GeV? Faktor 75000 Unterschied. Ernsthaft jetzt?
Ich bin mir sogar ziemlich sicher, dass ich da was nicht völlig verstanden habe… 🙁 Ich dachte immer, Energie-Masse bleibt im Rahmen der Unschärferelation erhalten.
@Alderamin:
„Ok, also sagst Du mir also, ein und dasselbe Teilchen kann bei einer Messung, je nachdem, wie die Wellenfunktion gerade zufällig kollabiert, mal 0,2 eV und mal 18,2 MeV Masse haben? „
Naja, das ist genauso abgefahren, wie die Idee, dass sich die unterschiedlichen Neutrino Sorten eben mal „irgendwie“ ineinander umwandeln und dann total unterscheidliche Massen haben …
Ich meine, was sollte sonst dahinter stecken?
Das die „Massenenergie“ eines Teilchens unterschiedliche Eigenwerte haben kann ist in der QFT jetzt nichts so exotisches soweit ich das verstanden habe – mein Verständnis geht da aber zugegebenermassen nicht wirklich sehr weit, daher würde mich auch interessieren wie man sich das genau vorstellen muss.
@Niels: Wenn du Zeit und Lust hast, dass mal kurz anzureissen wären sicher nicht nur @Alderamin und ich dankbar!
@Alderamin
Wenn er streng nach den Vorgaben der Unschärferelation vorgeht, hat er recht. Denn diese behauptet, dass erst die Messung das Ergebnis determiniert (Schrödingers Katze).
Mir persönlich würde jedoch die Annahme, dass ein deterministischer Zustand gegeben ist, der jedoch fluktuieren kann, besser gefallen würde, als diese indeterministische Kopenhager Deutung. 😉
WL01:
„Mir persönlich würde jedoch die Annahme, dass ein deterministischer Zustand gegeben ist, der jedoch fluktuieren kann, besser gefallen würde, als diese indeterministische Kopenhager Deutung. ;-)“
????
Was meinst du mit „fluktuieren“?
Bei der Schrödinger-Gleichung fluktuiert so gar nix.
Verstehe ich nicht ….
@Alderamin
kaum, da dann die energie- und impulsunschärfe groß genug sein muss, dass auch tatsächlich beide masseneigenzustände propagieren können. aber nachdem es kein neutrino mit einer masse von 18,2 MeV gibt (es wurde schon geschrieben, die oberen schranken sind nur so groß, weil die experimente für myon und tau derzeit noch so unpräziese sind. wir wissen, dass die unterschiede zwischen den drei neutrinomassen in wirklichkeit minimal sind), stellt sich die frage eigentlich auch nicht.
aber im prinzip passiert bei den neutrinos genau das: der zustand (das teilchen) ist eine überlagerung von drei verschiedenen massen. könnte man in einer messung auf einen masseneigenzustand testen (was man heute eben nicht kann), dann würde der zustand in eben genau diesen gemessenen masseneigenzustand kollabieren.
da bei den quarks die massendifferenz VIEL größer ist, gibt es bei quarks auch keine derartigen oszillationen (davon abgesehen, dass es sowieso keine frei propagierenden quarks gibt). aber bindungszustände aus quarks können oszilieren, da zwischen den beiden zuständen zwischen denen osziliert wird der massenunterschied wieder sehr sehr klein ist (namentlich die K,D und B mesonen).
deshalb (d.h. weil der masseneigenzustand des quakrs wohl immer eindeutig festgelegt sein wird) und weil außerdem die mischung bei den quarks viel geringer ist (d.h. jeder masseineigenzustand entspricht fast genau einem flavoreigenzustand, siehe das verlinkte bild in #107 von Niels), stiftet der unterschied zwischen flavor- und massenzustände hier gewöhnlich weniger verwirrung. man denkt einfach immer in masseneigenzuständen, die unterschiedliche wahrscheinlichkeiten haben mit den anderen generationen über die schwache wechselwirkung zu wechselwirken. so spricht man z.B. einfach von einem u-quark (ohne auf die unterscheidung zwischen massen- und flavorzuständen zu achten, aber eigentlich ist es in diesem sprachgebrauch dann ein masseneigenzustand), welches fast ausschließlich mit d-quarks wechselwirkt, nur ganz wenig mit s-quarks, und so gut wie gar nicht mit b-quarks. diese unterschiedlichen wahrscheinlichkeiten drücken eben die unterschiedlichen anteile der flavorzustände im massenzustand des u-quarks aus.
bei den neutrinos kann man aber erstens die masseneigenzustände nicht getrennt betrachten (da sie viel zu nahe beisammen liegen) und außerdem sind sie viel stärker gemischt.
@Alderamin
Hm, die Quarks hätte ich nicht ohne Not mit hinein bringen sollen.
Es gibt keine Quark-Oszillation entsprechend zur Neutrino-Oszillation. Das hab ich oben falsch behauptet, muss ein Blackout gewesen sein.
Das liegt aber nur daran, wie Quark und Neutrino definiert wurden.
Ein Quark wird über den Masseneigenzustand definiert. Ein up-Quark ist also ein Quark mit einer ganz bestimmten Masse.
Ein Neutrino wird dagegen über seinen Flavour-Eigenzustand definiert. Ein Elektron-Neutrino ist ein Neutrino mit dem „Elektron-Flavour“.
Die schwache Wechselwirkung lässt sich in geladene Ströme und ungeladene Ströme unterscheiden.
Durch die Definition der verschiedenen Quarks über die Masseneigenzustände entsteht der Nachteil, dass Quarks verschiedener Generationen über den geladenen Strom wechselwirken können. Wir können also nicht sicher vorhersagen, welches Quarks bei Wechselwirkungen über geladene Ströme erzeugt werden, sondern nur Wahrscheinlichkeiten angeben.
Bei Neutrinos wissen wir dagegen wie gesagt sicher, welches Neutrino erzeugt (oder vernichtet) wird.
Man hätte Neutrinos natürlich auch analog zu den Quarks oder Quarks analog zu den Neutrinos definieren können, das wäre vermutlich weniger verwirrend gewesen.
Allerdings dachte man ja, dass alle drei Neutrinos masselos wären. Da war eine Definition über den Flavour natürlich sinnvoller 😉 und das hat man dann beibehalten.
Dazu kommt, dass die Quarks sehr viel weniger mischen als die Elektronen. Wenn du dir das Schaubild
noch einmal anschaust, siehst man bei den Quarks auf den ersten beiden Balken kein Gelb und auf dem letzten Balken kein rot und kein blau.
Wenn die Quarks analog zu den Neutrinos definiert wären: Ja.
Wobei das aber wahrscheinlich nicht beobachtet werden könnte, weil so etwas absolut fantastisch unwahrscheinlich wäre.
Da Quarks aber über die Masse-Eigenzustände definiert werden: Nein.
Ja. Mit von Reggid erwähnten Einschränkung.
Ist eigentlich auch nicht seltsamer, als dass sich die Katze vorher im Überlagerungszustand zwischen tot und lebendig befand.
Ist auch so.
Jetzt habe ich aber eigentlich nichts gesagt, was Reggid nicht auch schon genannt hat. Ich wollte das aber noch mal mit besonderer Deutlichkeit herausstellen.
@Reggid
Habe ich eigentlich bei der obigen Erklärung der Neutrino-Oszillation irgendwo groben Unsinn erzählt oder kann man das so stehen lassen?
@PDP10
Sorry, da kenne ich mich leider auch nicht gut genug aus, um mich da aus dem Fenster zu lehnen.
@WL01
Na ja, ich glaube nicht, dass es verständlicher wird, wenn wir jetzt auch noch ohne Not über andere Interpretationen sprechen.
Kopenhagen ist ja durchaus die „Standardsprache“, in der man diskutiert. Ganz unabhängig davon, ob man Anhänger ist oder nicht.
Ähmm, allem Anschein nach gibt es bei Neutrinos (und ungeladenen Teilchen allgemein) in Materie einen der Tscherenkow-Strahlung ähnlichen Effekt:
https://en.wikipedia.org/wiki/Askaryan_effect
Wahrscheinlich werden Neutrinos vor allem mit Elektronen interagieren, und da beide linkshändig sind, handelt es sich dann um geladene Ströme, und deren Austauschteilchen sind elektrisch nicht neutral:
https://de.wikipedia.org/wiki/W-Boson
D.h. man hat schon aufgrund der allgemeinen Theorie sekundäre Ladungsträger, ganz unabhängig von irgendwelchen „non-local charge structure“ oder so.
Ansonsten interagieren Neutinos ja nicht nur über die schwache Wechselwirkung, sondern auch über die Gravitation.
@Niels:
„Sorry, da kenne ich mich leider auch nicht gut genug aus, um mich da aus dem Fenster zu lehnen.“
Nu stell mal dein Niveau nicht so unter den Scheffel.
Deine Erklärung oben hat eigentlich alle meine Fragen beantwortet die ich dazu hätte.
@Reggid, Niels
Also muss die Masse doch im Rahmen der Unschärferelation ähnlich genug sein, damit mit hinreichender Wahrscheinlichkeit zwischen verschiedenen Teilchen oszilliert werden kann (und die Unschärferelation besagt ja auch, dass große Unschärfen nicht unmöglich, sondern nur extrem unwahrscheinlich sind). Das ist aber eigentlich genau das, was ich in # 104 sagte und was Niels zu meiner Verwirrung in Zweifel zog.
@Reggid
Ich hatte in #74 spekuliert, dass man wohl auf das Vorhandensein einer Masse der Neutrinos aufgrund der Oszillationen schließt, weil masselose Teilchen sich mit Lichtgeschwindigkeit bewegen und somit keine definierte Eigenzeit haben, in der irgendwas oszillieren könnte. Stimmt das eigentlich, oder was ist das Argument, das die Masse aus den Oszillationen begründet?
[…] übrigens hier.) Da sich kein Körper relativ zu einem anderen mehr als lichtschnell bewegen kann (Spekulationen über Tachyonen lasse ich mal außen vor…), kann also kein Körper dem Schwarzen Loch […]
@Alderamin
Na ja. Nein, eigentlich überhaupt nicht.
Der Einfachheit halber nehmen wir mal an, dass es nur zwei Neutrinos gibt und wir uns die Sache im Vakuum anschauen.
Wir betrachten im „Neutrino oscillation“-Wikipediaeintrag also die Formeln unter „2.3 Two neutrino case“ und das Schaubild unter „3.1 Two neutrino probabilities in vacuum“.
Wie man sieht geht die Massendifferenz der beiden Neutrinos nur in die Phase ein. Ist die Massendifferenz doppelt so groß, verdoppelt sich einfach die Frequenz.
Hier wird ein Neutrino mit dem Flavour „A“ erzeugt. (Die Wahrscheinlichkeit für ein A-Neutrino ist im Schaubild bei x=0 gerade 1.)
Nach x = ungefähr 1100 würde man bei einer Messung mit Sicherheit ein A-Neutrino detektieren.
Verdoppelt sich durch Magie jetzt die Massendifferenz, detektiert man bei x = 1100 immer noch mit Sicherheit das A-Neutrino. Diesen Fall gibt es jetzt aber auch schon bei x = 550, usw.
Das habe ich hier mal als Plot dargestellt. Aus der blauen Kurve wird die lila Kurve.
Genauso verändert sich auch die rote Kurve im Wiki-Schaubild.
Es ist also ganz egal, wie groß die Massendifferenz ist. Das Neutrino oszilliert immer noch zwischen den beiden Flavour-Zustanden. Bei einem größeren Unterschied der beiden Massen oszilliert es einfach schneller.
Entsprechend, nur komplizierter, gilt das dann auch für drei Neutrinos. Die Formeln und Schaubilder dazu findet man wieder im Wikipedia-Eintrag.
Verzehnfacht man jetzt etwa die Masse des Myon-Neutrinos und verhundertfacht die das tau-Neutrinos, detektiert man ein Neutrino, dass als Elektron-Neutrino erzeugt wurde, immer noch nach bestimmten Zeiten (bzw. zurückgelegten Strecken) mit einer gewissen Wahrscheinlichkeit als jedes andere der beiden Neutrinos.
Die Wahrscheinlichkeiten dafür werden auch eigentlich nicht geringer. So werden einfach anders, die Wahrscheinlichkeitsverteilung ist jetzt einfach eine völlig andere.
Zur Erläuterung mal als Beispiel:
Wenn man ein als Elektron-Neutrino erzeugtes Neutrino fünf Stunden nach der Erzeugung misst, findet man zum Beispiel mit einer Wahrscheinlichkeit von 20% ein Elektron-Neutrino, von 70% ein Myon-Neutrino und von 10% ein Tau-Neutrino.
Nach der angesprochenen magischen Veränderung der Massen misst man dagegen ein als Elektron-Neutrino erzeugtes Neutrino fünf Stunden nach der Erzeugung zu 5% als Elektron-Neutrino, zu 20% als Myon-Neutrino und zu 75% als Tau-Neutrino.
(Die Zahlen sind spontan ausgedacht, es geht ja nur ums Prinzip).
Das sind die Wunder der Superposition. Daran muss man sich einfach gewöhnen.
Kann man vermutlich so sehen. Aus einer Nichtdefiniertheit Schlüsse zu ziehen ist aber ein bisschen seltsam und gewagt.
Tatsächlich ist die übliche Argumentation einfacher. Wenn die Neutrinos masselos wären, gäbe es keine verschiedenen Masse-Eigenzustände, es läge also auch keine Superposition vor und die Neutrinos könnten deswegen auch nicht zwischen verschiedenen Flavours oszillieren.
@Trottelreiner
Danke, diesen Effekt kannte ich noch nicht. Im Vakuum gibt es allerdings keine Elektronen, mit denen überlichtschnelle Neutrinos interagieren könnten.
@Niels
Also nochmal (sehr hilfreich war der Abschnitt „Theory“ im Wiki-Artikel; die Formeln danach nützen mir überhaupt nichts, ich verstehe nicht mal die Schreibweisen):
Oszillieren tun auch Quarks, nur wegen der großen Massendifferenz viel schneller als Neutrinos. Bei Neutrinos kann man über eine gewisse Entfernung von der Quelle mit großer Zuverlässigkeit beobachten, dass ein bestimmter neuer Neutrino-Flavour herauskommt, weil eben die Wellenlänge der Schwebung so groß ist. Beim Quark wäre das über mikroskopisch kurze Distanzen (bzw. Zeiten, Quarks sind ja auch viel langsamer unterwegs) der Fall.
Angenommen, der Flavour wäre die Farbe einer 3-farbigen LED, die von einer Elektronik mit einer bestimmten Geschwindigkeit umgeschaltet werden kann und man kann mit einem Knopfdruck diesen Wechsel anhalten und die aktuelle Farbe messen. „Neutrino-LEDs“ wechseln dann so langsam die Farbe, dass man anfangend bei immer der gleichen Farbe (etwa grün) und mit der Stoppuhr nach 5 Sekunden den Stop-Knopf drückend immer z.B. die Farbe „rot“ fände.
Bei „Quark-LEDs“ erfolgte der Farbwechsel hingegen rasend schnell. Wenn man dann irgendwann auf den Knopf drückt, hat man eine mehr oder weniger zufällige Farbe. Hätte man einen Moment später gedrückt, wäre eine ganz andere Farbe herausgekommen.
Das hieße, wenn ich ein bestimmtes Quark im Flavour messen könnte und kurz darauf noch einmal, dann käme ein anderes Flavour heraus, ein Up wäre plötzlich ein Charm. Habe ich das richtig verstanden?
Nein, kann nicht sein, weil Du ja sagst, es wäre extrem unwahrscheinlich:
Wie kommt denn jetzt die Wahrscheinlichkeit in die Rechnung, wenn die Massendifferenz doch nur die Frequenz bestimmt?
Reggid sagte doch auch:
Verwirrung.
@Niels:
Weswegen ich auch ein paar gefühlsmäßige (ja, bei Quantendings ein schlechter Anhaltspunkt) Probleme mit der Vakuum-Tscherenkow-Strahlung habe… 😉
Andererseits ist das Vakuum ja nicht wirklich leer, siehe Vakuumenergie, allerdings entstehen wohl eben nicht einfach laufend Teilchen aus dem Nichts:
https://scienceblogs.de/hier-wohnen-drachen/2013/08/13/die-vakuumenergie-und-der-casimir-effekt/
Vielleicht könnte man die Vakuumfluktuationen aber trotzdem bei der Berechnung verwenden. Ja, ich weiß, gefühlsmäßig ist weniger als mäßig. 😉
Sorry, kein Füssiker, mit denen spreche ich sonst eher über Tolkien und norwegischen Black Metal…
@Alderamin
Es gibt keine “Quark-LEDs”.
Das liegt daran, dass man Quarks nicht über ihre Farbe charakterisiert, sondern über ihre Masse.
Das hätte man zwar auch anders machen können, hat man aber nicht.
Deswegen oszillieren die „Farben“ von Quarks nicht.
Nochmal der Unterschied zwischen Neutrinos und Quarks in Bezug auf die schwache WW:
Ein Elektron-Neutrino und auch jedes andere Neutrino hat keine bestimmte, klar festgelegte Masse.
Deswegen ist es eigentlich Unsinn, von der Masse eines Elektronneutrinos zu sprechen. Masse-Eigenzustände und „Neutrino-Schwache-Wechselwirkung“-Flavour-Eigenzustände stimmen nicht überein.
Die verschiedenen Neutrinos werden über ihren Leptonen-Flavour, also ihren „Neutrino-Schwache-Wechselwirkung“-Flavour definiert.
Deswegen weiß man genau, welche Sorte von Neutrino bei einer Wechselwirkung bzw. Messung erzeugt oder vernichtet wird. Die WW funktioniert ja schließlich über den Flavour.
Neutrinos werden also bezüglich ihres Verhaltens während der schwachen WW sortiert. Man weiß sicher, wie ein Elektron-Neutrino schwach wechselwirkt.
Ein up-Quark und jedes andere Quark hat dagegen eine ganz bestimmte Masse. So sind die verschiedenen Quarks definiert.
Dafür ist dann der „Quark-Schwache-Wechselwirkung“-Flavour nicht festgelegt.
Masse-Eigenzustände und „Quark-Schwache-Wechselwirkung“-Flavour-Eigenzustände stimmen nicht überein. (Die „Quark-Schwache-Wechselwirkung“-Flavour-Eigenzustände heißen übrigens d‘, s‘ und b‘.)
Quarks werden also nicht(!) bezüglich ihres Verhaltens während der schwachen WW sortiert. Deswegen kann man nicht mit Sicherheit sagen, wie etwa ein up-Quark schwach wechselwirkt, sondern nur Wahrscheinlichkeiten angeben.
“Neutrino-LEDs” wechseln die Farbe aber gar nicht. Die “Neutrino-LED“ befindet sich stattdessen in einer Überlagerung aller drei Farben, also in einer Superposition.
Die LED weist ein Farbgemisch auf.
(Dieser Vergleich hinkt aber, für das quantenmechanische Phänomen der Superposition gibt es eben kein wirklich gutes makroskopisches Analogon.)
Was vielmehr mit der Zeit wechselt, ist der „Anteil der verschiedenen Farben“ in dieser Überlagerung, also im Farbgemisch
Wenn das Gemisch zu dem Zeitpunkt, zu dem ich den Kopf drücke, gerade zu 20% aus rot, zu 30% aus gelb und zu 50% aus grün besteht, zeigt die LED nach dem Drücken mit einer Wahrscheinlichkeit von 20% rot, von 30% gelb und von 50% grün.
((Genauer sind es die Wahrscheinlichkeiten die Betragsquadrate der Wahrscheinlichkeitsamplituden, das ist für diese Veranschauung aber öllig egal. Ich will nur nicht ohne Anmerkung etwas eigentlich falsches stehen lassen.))
Die drei Anteile am Gemisch bzw. diese Wahrscheinlichkeiten oszillieren mit der Zeit mit bestimmten Frequenzen.
Wenn ich den Knopf drücke und dann die Farbe rot leuchtet, bedeutet das nicht, dass auch in Zukunft einfach weiter die Farbe rot leuchtet. Stattdessen geht die LED anschließend wieder in einen zeitabhängigen Mischzustand über.
Wenn man den Knopf in Nullzeit zweimal drückt (blöde Analogie), ist das Ergebnis des zweiten Knopfdrucks natürlich wieder rot. Die Wahrscheinlichkeit für rot war also erwiesenermaßen 100%. Da die Wahrscheinlichkeiten mit fester Frequenz oszillieren, ist nach einer Periode und mehrfachen dieser Periode, also nach bestimmten Zeitdauern, die Wahrscheinlichkeit immer wieder 100%.
Das Gleiche gilt natürlich auch für alle anderen Zusammensetzungen.
(Eine Wahrscheinlichkeit von 100% für rot bedeutet aber nicht, dass die LED auch ohne Knopfdruck rot zeigt.
Es bedeutet stattdessen nur, dass bei Drücken des Knopfes garantiert rot angezeigt wird.
(Hier versagt wieder die Anschauung. Das ist eigentlich auch eine philosophische Geschichte und das gerade Gesagte gilt für die Kopenhagener Deutung. Andere Interpretationen der Quantenmechanik machen dazu andere aussagen.))
Moment, bei deiner Frage ging es um die Energie, nicht um die Farbe. Da ist das Ganze ein bisschen anders.
Wie gesagt, Neutrinos sind über ihren „schwachen Wechselwirkungsflavour“ definiert, Quarks über ihre Masse. Wobei man das bei Quarks dann verwirrenderweise auch flavour nennt, obwohl es um etwas anderes geht. Flavour ist nämlich eigentlich nur ein Sammelbegriff für Sorte.
Darüber, wie man eine Sorteneinteilung erhält, sagt der Begriff nichts.
Die Frequenz der Neutrino-Flavour-Wahrscheinlichkeitsveränderung. Das hat mit der Masse nichts zu tun.
@Alderamin
@Niels
Verstehe ich nicht ganz so( wenn ich’s nicht völlig falsch verstehe). Die Graphiken im Wiki für „Three neutrino probabilities“ zeigen das eigentlich ganz anschaulich. Wenn ein bestimmtes Neutrino( e.g. $latex \nu_e$ ) erzeugt wird so ist es nach entsprechender Periode(long range) wieder mit Wahrscheinlichkeit 1 als Neutrino des selben Typs(/Sorte) detektierbar. Zu jedem anderem Zeitpunkt sind die Wahrscheinlichkeiten (für jeden Typ) < 1 . Von daher wäre auch „zweimaliges (LED-)Drücken in Nullzeit“ nicht zwangsläufig mit dem selben Ergebnis beschieden. Mit Wahrscheinlichkeit = 1 (also fast sicher) hat man das ja nur für den Fall, daß das Knopf-drücken mit der Periode zum Erzeugungszeitpunkt zusammentrifft. Umgekehrt würde dies ja sonst bedeuten, daß ein Neutrino stets als solches erzeugt worden wäre wie es(zu einem beliebigen Zeitpunkt) detektiert wird.
Na ja, mit F= U*M und da U unitär erhält man ja schon M = U^t *F und so durchaus auch eine „Massen-Wahrscheinlichkeitsveränderung“ … 🙂
@StefanL
Und genau das habe ich zu schreiben vergessen. 😉
Danke, so ist es wirklich unklar.
Gnagnagna.
Mein Problem ist, dass ich Die Graphiken im Wiki für “Three neutrino probabilities” zeigen das eigentlich ganz anschaulich. eigentlich ebenfalls finde und ich nicht weiß, wie ich es Alderamin besser als bisher schon versucht erklären soll.
#130 war da nochmal ein zusätzlicher Versuch, der anschaulicher werden sollte. Da steckt ja überhaupt nichts Neues drin. Die bessere Anschaulichkeit fällt mir aber nicht besonders leicht. Ich habe schon selbst beim Schreiben bemerkt, dass da Probleme mit der genauen fachlichen Korrektheit passieren.
Ist dir klar, woran es bei Alderamin noch hängt? Vielleicht kannst du es ihm ja besser erklären? Ich bin wohl leider gescheitert.
@Niels
das problem bei dem wikipedia artikel und der formel zur neutrino oszillation mit zwei flavors ist, dass hier nur mit ebenen wellen gerechnet wird. dieser ansatz führt zwar tatsächlich zur korrekten formel für die oszillationslänge, ist aber dennoch für eine realistische situation nicht praktikabel und vernachlässigt eben genau die dekohärenz effekte aufgrund zu großer massenunterschiede auf die ich angespielt habe, als ich geschrieben habe dass keine oszillation beobachtbar ist wenn die impulsunschärfe nicht groß genug ist.
der grund ist, dass ebene wellen zustände mit exakt definierter energie und impuls sind und eine unendliche ausdehnung haben (d.h. sie sind auf einen einzelnen wert gepeakt im impulsraum und unendlich weit ausgedehnt im ortsaum). beides ist erstens unrealistisch (auch wenn ebene wellen eine oft verwendete und auch oft sinnvolle näherung in der quantenmechanik sind) und zweitens nicht mit oszillationen vereinbar. denn da die masse eindeutig durch energie und impuls festegelt ist (m^2=E^2-p^2 in natürlichen einheiten), ist für eine ebene welle mit scharfem impuls und energie auch die masse exakt festgelegt. damit kann es sich aber nicht mehr um eine überlagerung mehrerer massenzustände handeln. auch im ortsraum hat man mit dieser beschreibung probleme, denn eine ebene welle hat wie gesagt eine homogenen, unendliche ausdehnung. dann kann man aber nicht mehr von oszillation sprechen, die ja besagt dass man am ort x1 diesen flavor, und am ort x2 jenen flavor misst. denn ein teilchen beschrieben durch eine ebene welle ist nicht erst an ort x1 und dann an ort x2, sondern immer und überall gleichzeitig. so macht das ganze keinen sinn.
als erste näherung sind ebene wellen zwar schon in ordnung, will man das ganze aber genauer beschreiben muss man zumindest mit wellenpaketen rechnen (und will man noch exakter sein, dann überhaupt quantenfeldtheoretische methoden verwenden). die rechnung mit wellenpaketen ist beschrieben in Phys. Rev. D 44 (1991) 3635, für diejenigen die zugang haben (ich habe leider keine frei verfügbare version des artikels gefunden, ist noch aus der vor-arxiv-zeit), sonst frei zugänglich eine zusammenfassung nochmal hier https://homepage.univie.ac.at/reinhold.bertlmann/pdfs/dipl_diss/Samitz_Bachelorarbeit.pdf (kapitel 2.3, die übergangswahrscheinlichkeit für den zwei-neutrino-fall mit den dekoährenztermen in Gl. 2.20)
das resultat ist, dass es keine oszillation gibt wenn die impulsunschärfe zu klein wird gegenüber der massendifferenz. man kann also die massendifferenz nicht einfach beliebig erhöhen und trotzdem noch oszillationen erwarten.
das kann man sich aber auch ganz einfach ohne rechnung und wellenpakete veranschaulichen, wenn wir wieder annehmen es gäbe nur zwei neutrino flavors und ein masseneigenzustand ist realistisch mit 1 GeV. wenn wir jetzt ein geladenes pion mit einer masse von ca. 130 MeV in ein myon und ein neutrino zerfallen lassen, so kann das neutrino in diesem zerfall nicht eine überlagerung aus beiden massenzuständen sein und daher auch nicht oszillieren (oszillation gibts ja nur wenn eine überlagerung besteht), denn der zustand mit einer masse von >1GeV kann bei einem zefall eines teilchens mit ~130 MeV schlicht nicht auftreten.
daher ist ein zu großer massenunterschied schon ein ausschlussgrund für oszillationseffekte, und daher oszillieren auch nur flavorzustände, deren massenzustände aus denen sie zusammengesetzt sind winzig kleine massendifferenzen aufweisen (nämlich neutrinos, K-, D- und B-mesonen).
@Alderamin
durch die messung der oszillationslänge bestimmt man die differenz der massenquadrate.
hätten alle die selbe masse, dann würden alle drei massenzustände gleich propagieren und daher würde es keine oszillation geben (denn die überlagerung würde 1 km hinter der quelle immer noch gleich ausschauen wie 10 km hinter der quelle, denn alle zustände propagieren ja exakt gleich). gibt es aber eine massendifferenz, dann gibt es kleine unterschiede in der zeitentwicklung der masenzustände. ihre phase (quantenzustände sind ja komplex) läuft ein bisschen anders, und daher ändert sich die exakte überlagerung der drei massenzustände periodisch mit der zeit, und daher wird aus einer überlegerung die ursprünglich exakt einem z.B. elektron neutrino entsprochen hat nach einiger zeit etwas, das auch mehr ähnlichkeit mit einem z.B. myon-neutrino hat.
aber ohne massendifferenz keine oszillation. dass wir also oszillationen zwischen allen drei neutrino flavors sehen können bedeutet, dass die drei massenzustände drei verschiedene massen haben. beachte dass der absolute betrag der masse hier in keiner weise eingeht. nur die differenz der massen. neutrino oszillationen belegen also streng genommen nur, dass zumindest zwei der drei massenzustände massiv sind, denn eigentlich könnte einer trotzdem noch masselos sein, das kann man nicht ausschließen.
@Niels
Ok, sehe ich ein, da hinkt der Vergleich etwas, ich weiß aber was eine Superposition und eine kollabierende Wellenfunktion ist. Gemeint war, rot ist Elektron-Neutrino, Grün ein Myon-Ny und Blau ein Tauon-Ny.
In den Schaubildern im Wiki-Artikel geht die blaue Kurve alle 1000 km/GeV immer wieder auf 1, d.h. genau an dieser Stelle würde man immer genau die gleiche LED-Farbe erhalten, dazwischen mit gewissen Wahrscheinlichkeiten auch andere, je nach dem was das Quadrat der Wellenamplitude für das jeweilige Teilchen gerade hergibt.
Ich meinte die LED-Farben auch nicht im Sinne der Farbladungen, sondern der Massen (bei den Neutrinos: Elektron-, Myon- und Tau-Ny, bei den Quarks z.B. Up/Charm/Top). Ich hatte überlesen, dass Du oben gesagt hast, Quarks oszillieren nicht in der Weise wie Neutrinos (wäre mir auch neu gewesen). Auf die Idee kam ich erst, weil Du sagtest, dass auch Quarks über die CKM-Matrix mischen würden und wegen des Arguments, dass die Oszillationsfrequenz von der Massendifferenz abhänge (die ja bei Quarks groß ist). Das hat mich einfach auf die falsche Fährte gebracht.
Was mischt die CKM-Matrix denn? Warum bei Quarks nichts oszilliert, hat Reggid ja in #133 erklärt, wenn ich ihn richtig verstanden habe.
@Reggid #134
Danke, habe ich verstanden. Keine Massendifferenz -> kein Frequenzunterschied.
@Reggid
Klasse, vielen Dank. Super erklärt.
Kann es sein, dass das auch in den üblichen Standard-Lehrbüchern falsch, also nur vereinfacht dargestellt wird? Ich bin mir ziemlich sicher, dass uns das schon in der Uni falsch beigebracht wurde. (Ist aber jetzt auch schon eine ganze Weile her.)
Man müsste aber auch mal dringend die Wikipedia überarbeiten. Ist ja eigentlich ein echter Skandal, dass dort dazu überhaupt nichts zu finden ist, nicht mal eine kurze Randbemerkung.
Wenn eine vereinfachte Darstellung so ein wichtiges Phänomen völlig übersieht und außerdem nicht mal darauf hingewiesen wird, dass es sich eben um eine stark vereinfachte Modell-Darstellung handelt, die den echten Sachverhalt nicht richtig beschreibt, ist das doch wirklich keine zu vernachlässigende Kleinigkeit.
@Alderamin
Da siehst du es mal, deine Intuition hat bessere Ergebnisse geliefert als meine (zu oberflächliche) Beschäftigung mit dem Formalismus und den gegebenen Formeln.
Natürlich muss man auch hier die Unschärferelation berücksichtigen. Wie Reggid anmerkt, müsste einem das eigentlich auch klar sein, wenn man sein Gehirn einschaltet.
Tut mir leid wegen der angerichteten Verwirrung. Zu diesem Aspekt habe ich leider ganz überzeugt völligen Unsinn erzählt.
Siehst du, man sollte mir eben nicht einfach Dinge glauben, ich liege auch gerne mal völlig daneben.
@Niels
also skandalös finde ich den wiki artikel (und die meisten lehrbücher, die in der tat meist nur mit ebenen wellen rechnen) eigentlich nicht. näherungen und vereinfacherungen sind nun mal das um und auf in der physik, vieles in der quantenmechanik wird studenten erst mal mit ebenen wellen beigebracht um zuerst nur die grundlegenden konzepte zu sehen, und gerade wikipedia ist ja keine fachzeitschrift. es steht ja zum glück nichts grundlegendes falsches drin, sondern nur eine vereinfachte darstellung, welche bei tiefergehenden fragenstellungen (wie denen von Alderamin, wie das jetzt genau bei größeren massenunterschieden ist) dann halt doch nicht mehr anwendbar ist. aber das ist ja normal. aber du hast recht, man hätte vielleicht deutlicher auf die grenzen dieses modells hinweisen können. andererseits kann man auch sagen, dass dieser artikel ausschließlich von neutrino oszillation handelt, und hier sind diese dekohärenzeffekte ja auch tatsächlich absolut vernachlässigbar (die massenunterschiede sind ja so gering, dass man nicht in gefahr läuft mal irgendwie einen reinen massenzustand zu präparieren). da wäre ein mathematisch aufwendigerer formalismus bloß für etwas, das dann eh komplett vernachlässigt werden kann wohl ein bisschen „mit kanonen auf spatzen schießen“. mir gings hier ja nur um die prinzipielle klarstellung des sachverhalts in der diskussion mit dir und Alderamin, nicht um echte neutrino oszillationen.
aber ich kann ich erinnern, dass ich, als ich mich zum ersten mal mit dem thema beschäftig habe, auch fast verzweifelt wäre ob der frage, wie das denn mit der energieerhaltung zu vereinbaren sein kann, dass ein physikalisches neutrino (flavorzustand), wie es bei einem zerfall ensteht, plötzlich mehrere verschiedene massen haben kann. da wäre dann ein kurzer hinweis in wikipedia auf die lösung des problems durch wellenpakete doch hilfreich gewesen.
@Niels:
„Man müsste aber auch mal dringend die Wikipedia überarbeiten. Ist ja eigentlich ein echter Skandal, dass dort dazu überhaupt nichts zu finden ist, nicht mal eine kurze Randbemerkung.“
Aha …
@Reggid:
„und gerade wikipedia ist ja keine fachzeitschrift. es steht ja zum glück nichts grundlegendes falsches drin, sondern nur eine vereinfachte darstellung, welche bei tiefergehenden fragenstellungen (wie denen von Alderamin, wie das jetzt genau bei größeren massenunterschieden ist) dann halt doch nicht mehr anwendbar ist. aber das ist ja normal. aber du hast recht, man hätte vielleicht deutlicher auf die grenzen dieses modells hinweisen können.“
Uuuund …. warum editiert ihr die entsprechenden Artikel in der Wikipedia jetzt nicht einfach?
Mir hat eure Diskussion mit Alderamin jedenfalls schwer weitergelholfen beim Verständnis des Themas.
Wenn ihr beiden jetzt nur noch 5% mehr von eurer Zeit, die ihr hier mit der Diskussion verbracht habt in die entsprechenden Wikipedia Artikel reinsteckt, helft ihr noch ein paar Tausend Leuten mehr und könnt bei zukünftigen Diskussionen dieser Art hier auch noch einfach darauf verlinken!
Win-Win-Situation!
@PDP10:
Zugegeben, es wäre sicher auch mal ein interessanter, wissenschaftlicher Test, die genaue Zeit zu stoppen, bis diese Änderung auf der deutschen Wikipedia von irgendwelchen Möchtegern-Blockwarten rückgängig gemacht würde. Aber Niels und Reggid sind doch keine Soziologen. Zumindest nehme ich das nicht an. 😉
Deutliche Hinweise/Belege für die CP-Verletzung https://arxiv.org/abs/1412.4673
@Reggid
Ist das so? Wir sind ja nicht in einer völlig Kontext freien Situation. Ausgehend von den Meßdaten ( en.wiki Neutrino oscillation Observed values of oscillation parameters ) funktioniert es nicht egal welche Masse = 0 gesetzt wird. Auch das(3×3)-Modell F = U * M liefert ja (e.g. mit m_3 = 0) , daß f_3 dann unabhängig von u_33 wäre( und damit 3 → 3 belanglos(?)) .
@Niels „Vielleicht kannst du es ihm ja besser erklären?“
Uhh – da stecken aber gleich mehrere Spekulationen drin( angefangen beim Verstehen dessen was ggfs. nicht verstanden ist bis hin zu einer möglicherweise erklärenden Theorie) 😉
Bei einer reinen Dirac-masse könnte ich mir eine Art Oszillation der Koppelung ans Higgsfeld spekulativ vorstellen – habe allerdings zuwenig Ahnung wie dies tatsächlich aussehen könnte.
@Reggid – könnte da das unterschiedliche Propagieren der Wellenpakete etwas Licht ins Dunkel bringen ( oder ist dies völliger Blödsinn)?
Und bzgl. Majorana-masse/ Seesaw-mechanismus ( da kommt auch wieder der eingangs erwähnte Artikel zur CP-Verletzung ins Spiel) befinden wir uns ja auf einem großen Spielfeld der Forschung. ( e.g. https://arxiv.org/pdf/1412.8352v1.pdf )
Also (imho): bzgl. der Überlagerung/Superposition – ist wohl geklärt.
Zusammenhang Oszillation/Massendifferenz – wohl auch geklärt
Unterschiedliche Massen(werte)/ Art von Massen( Majorana, Dirac) – Forschungsfeld.
@StefanL
ich sehe nicht, warum eine masse nicht 0 sein können sollte. die masse geht nirgends ein (nur die differenzen), also kann darüber doch gar keine aussage gemacht werden.
ich finde die notation ein bisschen verwirrend bzw. ich glaube ich habe sie nicht verstanden. F ist ein vektor mit den flavorzuständen, M die massenzustände und U die PMNS matrix? und sind f_i, m_i und u_ij dann die einzelnen komponenten? aber warum setzt du dann m_3 = 0? oder ist m_i die masse? aber dann weiß ich leider auch nicht worauf du hinaus willst.
was ist denn überhaupt „dunkel“?
@nanda
Eine Änderung muss mittlerweile erst von ein Wiki-Admin freigeschaltet werden, damit kein Vandalismus betrieben werden kann.
Wenn man seine Aussage mit einer Quelle belegt, schalten die das an einem Tag frei.
@Reggid
Na ja, wenn bei einem Modell mal eben die Energieerhaltung unter den Tisch fällt, muss man das meiner Ansicht nach schon extra deutlich machen.
@Alderamin
Ja, genau. Das steht hoffentlich zu nichts in Widerspruch, was ich geschrieben habe? Sonst habe ich mit einfach zu dämlich ausgedrückt.
Quarks. 😉
Sie gibt an, wie stark ein bestimmtes Quark mit den passende Quarks der verschiedenen Generationen wechselwirkt.
Nämlich sehr stark mit dem Quark seiner eigenen Generation (also zum Beispiel mit dem down-Quark, wenn es um das up-Quarks geht), weniger mit der nächsten Generation und praktisch gar nicht mit der verbleibenden Generation.
(Um so unähnlicher die Massen, um so unwahrscheinlicher.)
[@Reggid
Das stimmt doch so, oder?]
@StefanL
Mir ist nicht richtig klar, was du mit dem letzten Beitrag sagen willst.
Mehrere Forscher wünschen sich eine größere Version des Super Kamiokande.
Was hat das mit deutlichen Hinweisen auf die CP-Verletzung zu tun?
Solche Hinweise haben wir doch außerdem schon, nämlich durch das Belle- und BaBar-Experiment.
Und neue Dinge werden wir durch NOνA in Erfahrung bringen. Das Ding steht nämlich schon.
Ob es wirklich irgendwann in den nächsten Jahrzehnten einen Hyper-Kamiokande steht doch noch völlig in den Sternen, oder?
Was wolltest du also sagen?
Ich verstehe auch nicht, wodurch deiner Meinung nach die Masse Null ausgeschlossen wird?
Man kann sich darüber streiten, ob das ein Finetuning-Problem darstellt, aber das ist eine ganz andere Baustelle?
@Niels
Da habe ich mich durchs abstract und das aktuelle Datum blenden lassen und “ will be “ und “ is expected “ schlicht überlesen…. Ist nicht mein Tag… Es ging mir auch nicht i.a. um CP-Verletzungen sondern speziell bei Neutrinos. Ja, wir können gespannt sein was NOvA findet.
Feintuning der Massebestimmung – ja … Mein Empfinden ist, dass 10^[-5] eV^2 (Spielerei mit mal diese oder jene Masse =0 gesetzt) weit genug weg von 0 ist…obwohl noch u.U. im Variationsbereich der Massendifferenzquadrate… Aber möglicherweise liege ich da falsch. Das letzte Wort hat da sicherlich das Experiment.
Zu theoretischen Überlegungen( irgendwoher kommt ja mein Empfinden) später mehr…
@141
Ja, Vektor der Flavour $latex F=(f_i)_{3,1}$, Vektor der Massen $latex M=(m_i)_{3,1}$ und U die unitäre Mischungsmatrix $latex U=(u_{ij})_{3,3,}$.
Falls nun eine Masse = 0 ist so sei dies $latex m_3=0$. Damit ist dann $latex \forall i:\quad f_i = u_{i1}\cdot m_1 + u_{i2}\cdot m_2$. Da U unitär ist, ist $latex m_i= \sum_j \bar{u}_{ji}f_j$. Und so insbesondere
$latex f_3 = u_{31}(\bar{u}_{11}f_1+\bar{u}_{21}f_2+\bar{u}_{31}f_3) + u_{32}(\bar{u}_{12}f_1+\bar{u}_{22}f_2+\bar{u}_{32}f_3)$
$latex = A(f_1,f_2) + |u_{31}|^2f_3 + B(f_1,f_2)+|u_{32}|^2f_3$
$latex \Rightarrow A+B=0 \wedge |u_{31}|^2+|u_{32}|^2=1$
So bleiben für $latex u_{33} \quad (da\; \sum |u_{ii}|^2=1)$ nicht mehr allzu viele Möglichkeiten. Scheint mir schwierig da dann den zugehörigen Zustand überhaupt festzustellen, wenn das Verbleiben in selbigen (stets)mit Wahrscheinlichkeit 0 belegt ist. Von daher wäre ( imho) im Falle eines (ruhe-)masselosen Neutrinos zumindest die Modellierung nicht passend.
was ist denn überhaupt “dunkel”?( @Reggid)
( 🙂 da kann ja glatt mal wieder einer der Witze über superluminare Neutrinos angebracht werden: Kommt ein superluminares Neutrino in eine Bar – und kracht voll gegen die Theke. Neutrino: “ Mist, ist das dunkel hier“ Barkeeper: “ Ja, das Licht ist noch nicht da.“ 🙂 )
Aber ernsthaft: Es geht doch um Ruhemassen(?) und da spielt doch (i.a.R.) die Koppelung ans Higgs-Feld eine Rolle(?). Und würde dies dann nicht bedeuten, daß das unterschiedliche propagieren der Wellenpakete einhergeht mit einer Oszillation eben dieser Kopellung ans Higgs-Feld? Und die Frage ( zu dessen was „dunkel“ ist) ist ob da die Betrachtung von Wellenpaketen dahingehend Einsichten vermittelt und wenn ja ggfs. welche( bzw. ob diese Fragestellung sowieso unsinnig ist).
@StefanL
nein, m_i sind nicht die massen, sondern die masseneigenzustände. daher ist m_3 auch nicht 0, bloß weil die dritte masse 0 ist.
Grüße aus Karlsruhe, ich guck mir das mal die Tage genauer an, danke für den Post sonst hätte ich es vmtl. nicht mitbekommen.
Bei KATRIN wird in der Tat das Massenquadrat gemessen und das Expriment wär bei einer hinreichend großen Tachyon-Masse auch sensitiv genug um darüber etwas zu sagen. KATRINs Messprinzip basiert übrigens nicht wie oftmals angenommen auf der Verschiebung des Spektrum-Endpunkts sondern auf der Form des Spektrums unter dem Endpunkt. Da die Kinematik für Tachyonen-Neutrinos eben etwas anders aussieht als für normale dirac (oder majorana) neutrinos, wird auch das Spektrum anders verzerrt.
Der Teufel steckt natürlich im Detail. Frühere Neutrinomassen-Experimente hatten auch negative Neutrinomassenquadrate als Ergebnis. Das passiert wenn man einen systematischen Fehler übersieht. Die Mainzer die das Vorgänger Experiment gebaut haben mussten sehr Tief in die Festkörperphysik ihrer kondensierten Tritiumquelle eintauchen bevor sie die Resultate ihrer Messung vollständig verstanden hatten. Wenn KATRIN also sowas misst, wären tachyonische elektron-neutrinos sicherlich nicht der erste erklärungsversuch, und auch nicht der zweite. Vorher lieber nochmal alle Kabel prüfen 😉
@Nikolaus
Danke für die fachkundige Info offenbar direkt von der Quelle. Wann geht’s denn los mit den Messungen und wann rechnet Ihr mit den ersten Ergebnissen?
@Reggid
Danke für den Hinweis, daß die a priori Annahme kanonischer Orthogonalität mit der (daher fälschlichen) Identifizierung $latex \left|\nu_i(0)\right\rangle=m_i$ nicht per se gerechtfertigt ist. Irritierenderweise wird das Propagieren der Massen-eigenzustände ( in den Wiki-Einträgen) auch nur bzgl. jeweils einer (Basis-)Masse beschrieben ( de.Wiki Neutrino Oszillation: $latex \left|\nu_i(L)\right\rangle=\left|\nu_i(0)\right\rangle e^{-i{\frac{m_i^2c^4}{2E}}\frac{L}{\hbar c}}$ ).
Sollte da dann nicht auch $latex \left|\nu_i(L)\right\rangle=(e^{-i{\frac{m_1^2c^4}{2E}}\frac{L}{\hbar c}}\vec{e_1},e^{-i{\frac{m_2^2c^4}{2E}}\frac{L}{\hbar c}}\vec{e_2},e^{-i{\frac{m_3^2c^4}{2E}}\frac{L}{\hbar c}}\vec{e_3})\left|\nu_i(0)\right\rangle $ geschrieben werden( o.ä.; wobei $latex \vec{e_i}$ dieEinheitsbasisvektoren seien)?
Jedenfalls folgt für $latex m_s=0$ doch dann, daß die dieser (Basis-)Masse zugeordnete( bzw. mit entsprechendem Faktor multiplizierte) Komponente in $latex \left|\nu_i\right\rangle\, (=\left|\nu_i\right\rangle(0)\,)$ im zeitlichen Verlauf unverändert bleibt. Massen-Eigenzustand (im „Massen-Raum“ ) bedeutet doch auch, daß $latex U \left|\nu_i\right\rangle = \lambda_i \left|\nu_i\right\rangle \, mit\, \lambda_i \in \mathbb{C}\; und\; \left|\nu_i\right\rangle= \sum_s k_{is}m_s \vec{e}_s $ mit bestimmten Konstanten $latex k_{is}$ ist.(?)
Und dies liefert (sofern nicht eine weitere Fehlüberlegung vorliegt) dann folgendes Argument gegen eine 0-Masse:
Jeder der (Massen-)Eigenzustände besitzt eine Komponente zu jeder der „Basis-massen“ $latex m_s$. Und eine weitere Eigenschaft der ( hier drei) Eigen-zustände ist ja, daß sie den gesamten „Massenraum“ aufspannen( da U unitär). Wäre jetzt für jeden der drei Eigenzustände stets die selbe (kanonische) Basis-komponente $latex k_{is}m_s \vec{e}_s= 0 \;( da\; m_s= 0 )$ so wäre es nicht möglich den gesamten Raum aufzuspannen.
Aber, wie schon zuvor mal angemerkt, da wird sicherlich das Experiment das letzte Wort haben um über ein (widerspruchsfrei erklärendes) Modell zu entscheiden…
[…] Sind Neutrinos schneller als das Licht? – Astrodicticum … – Die sechs Punkte entsprechend seiner Auswertung der Daten und geben die Neutrinomasse an. Innerhalb der Fehlerbalken stimmen sie überein und geben eine …… […]