Dieser Gastartikel ist ein Beitrag zum ScienceBlogs Blog-Schreibwettbewerb. Alle eingereichten Beiträge werden im Lauf des Septembers hier im Blog vorgestellt. Danach werden sie von einer Jury bewertet. Aber auch alle Leserinnen und Leser können mitmachen. Wie ihr eure Wertung abgeben könnt, erfahrt ihr hier.
Dieser Beitrag wurde von Peter Hank eingereicht.
———————————————————————————————————————–
Diese Frage ist der Titel eines Vortrags, den ich vor kurzem für die Volkshochschule München gehalten habe. Bevor ich die Frage beantworte, möchte ich kurz die Vorgeschichte zur Frage (und zum Vortrag) erzählen.
Ich selber komme aus der Physik und dort stellt sich diese Frage normalerweise nicht. Theorien
werden aufgestellt, Experimente gemacht und am Ende des Tages werden Theorien, die den Experimenten widersprechen, verworfen. Wie Thomas H. Huxley gesagt hat:
Oft schmerzlich, wenn die eigene Lieblingstheorie den Bach runter geht, aber mit dem Experiment als unbestechlichen Richter hat die Naturwissenschaft die einzigartige Möglichkeit, Theorien objektiv zu prüfen und falsche Theorien zu erkennen und zu entsorgen. Dieser Reinigungsprozess funktioniert sehr gut und so ist die Physik bisher von Pseudowissenschaften weitgehend verschont geblieben. (Hier muss ich gleich einen Seitenhieb loswerden – im Gegensatz zur Medizin werden unbewiesene oder widerlegte Inhalte an den Unis in Physik nicht gelehrt; so gibt es keine Kurse für Astrologie oder Rutengehen an den Hochschulen.)
Vor diesem Hintergrund ist es für mich zutiefst verwunderlich, aber auch faszinierend, warum sich, – in meinen Augen offensichtlich fragwürdige bis hin zu völlig absurde Ideen – Ideologien, Verschwörungstheorien,
Alternativmedizinische Verfahren, Glaubenssysteme – trotzdem weitgehender Anerkennung und Beliebtheit erfreuen.
Und natürlich stellt sich mir die unangenehme Frage: Gibt es eigene Vorstellungen, bei denen ich genauso an absurde Ideen glaube und es nur selber nicht merke, weil mein Hirn mir sagt, dass wäre alles vernünftig und in Ordnung. Kurz:
Kann ich meinem Hirn trauen?
Die Frage hört sich schon mal absurd an; genau so könnte ich mich fragen, ob ich meinen eigenen Augen trauen kann?
Halt – auch wenn
wir Sätze sagen wie „ich habe es mit eigenen Augen“ gesehen, dann haben wir alle schon optische Täuschungen erlebt, die unsere Augen und unser Hirn an der Nase herumführen.
Viele dieser Täuschungen nutzen künstliche Situationen aus, die in der wirklichen Welt nicht vorkommen. Da unser Hirn aber seit Millionen von Jahren darauf eingestellt ist, sich in einer dreidimensionalen Welt zurechtzufinden, kann man diese „eingebauten“ Mechanismen nutzen, um dem Hirn auch eine Scheinwelt vorzuspiegeln.

Ein anderer Typ von Täuschung nutzt die Fähigkeit des Hirns aus, aus unvollständigen Hinweisen komplette Muster zu erkennen.

Für einen Höhlenmenschen ist diese Fähigkeit überlebenswichtig gewesen, schließlich reicht es nicht, den Tiger erst zu erkennen, wenn er aus dem Busch rausgelaufen kommt. Allerdings kann diese, an sich nützliche Fähigkeit dann dazu führen, dass das Gehirn – auf Sicherheit bedacht – auch schon mal Muster erkennt, wo keine da sind. Am schönsten lässt sich dieser Effekt bei Gesichtern demonstrieren (Pareidolie), schließlich ist das Erkennen von Gesichtern besonders überlebenswichtig (könnte ja ein Feind oder Freund bzw. Paarungspartner sein).

Genauso wie diese optischen Täuschungen gibt es kognitive Täuschungen und auch die führen zum Beispiel dazu, dass wir Muster sehen, wo keine sind. Ein klassisches Experiment dazu hat P. C. (On the Failure to Eliminate Hypotheses in a Conceptual Task, The Quarterly Journal of Experimental) durchgeführt. Versuchspersonen wurden dazu gebeten, herauszufinden, nach welchem Gesetz Reihen von drei Zahlen gebildet wurden. Vorgegeben war die Reihe 2, 4, 6 und ein typischer Verlauf war etwa wie auf der Tafel dargestellt:
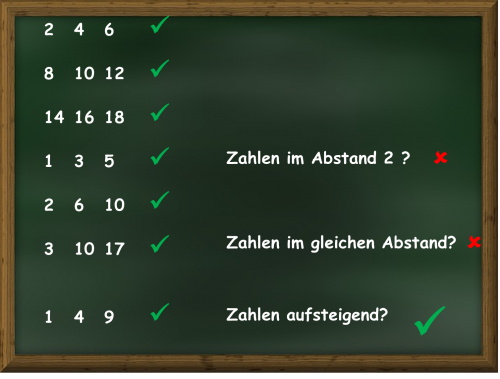
Nach den ersten Versuchen mit 8, 10, 12 (korrekt), 14, 16, 18 (korrekt) und 1,3,5 (korrekt) hat die Versuchsperson die Regel formuliert, man müsste zur ersten Zahl jeweils 2 addieren – diese Regel, obwohl sie bei allen Versuchen korrekte Zahlenreihen erzeugt war aber nicht die richtige. Auch der zweite Versuch (gleiche Abstände) führte nicht zur richtigen Regel.
Tatsächlich ist es schon ausreichend, wenn die Zahlen aufsteigend aufgereiht sind.
Was man aus diesem Experiment lernt:
– Unser Hirn neigt dazu, nach Mustern zu suchen und diese auch zu finden.
– Dabei schießt es gern über das Ziel hinaus und findet Muster, wo keine sind.
– Nur selten versucht eine Versuchsperson, ihre Regel dadurch zu prüfen, dass es nach Gegenbeispielen zur Regel sucht. Dabei hätte das dazu geführt, aufzudecken, dass die Regel viel zu eng gefasst war. (Eine dementsprechend große Rolle spielt daher auch die Falsifizierbarkeit in der Naturwissenschaft, aber das ist dort – ich möchte sagen – antrainiert, unsere automatischen Reflexe gehen, wie oben gezeigt, in eine andere Richtung.)
Warum ist dieses Experiment für uns auch für unser tägliches Leben relevant?
Weil wir auch dazu neigen, im täglichen Leben Muster zu finden und an diesen festhalten, ohne sie jemals zu prüfen. Wenn wir an die letzte Fußballweltmeisterschaft zurückdenken, dann erinnern wir uns vielleicht
an den deutschen Fußballtrainer Joachim Löw und seinen blauen Glückspulli? Wer hat nicht schon davon gehört, dass bei Vollmond mehr Kinder zur Welt kommen? Wer glaubt, dass bei ihm die Ampel immer rot ist? Wem wurde noch kein Schnupfenmittel angeboten (Hühnersuppe, Zuckerkügelchen, …) mit dem Satz „Bei
mir hat es geholfen!“.
Gemeinsam ist dem, dass unser Hirn eine interne Strichliste führt, die jedes Mal und auch nur dann, wenn unser Muster bestätigt wird, eine zusätzlichen Strich erhält.
Ein Freund von mir hat dazu das Bild geprägt vom
Glauben an ein Phänomen gleicht einer Ratsche
– jedes passende Beispiel dient nur dazu den Glauben fester zu ziehen und
– Gegenbeispiele werden nicht mehr registriert.
Der wissenschaftliche Begriff dafür ist Bestätigungsfehler oder Confirmation Bias und besagt eben gerade, dass wir dazu neigen, nur die Informationen wahrzunehmen und zu berücksichtigen, die unsere vorgefasste Meinung stützen. Warum ist das ein Problem?
Stellen Sie sich bitte vor, sie wären ein Mediziner und kommen 1846 an eine Klinik, etwa Wien. Dort wird nach einem bestimmten Verfahren gearbeitet, für unser Beispiel Geburtshilfe. Wenn Sie rumfragen, ob
die Behandlung etwas taugt, heißt es:
„Ja, wir hatten dieses Jahr 4010 Fälle, in denen es geholfen hat.“
Wenn Sie sich an das obige Beispiel Bestätigungsfehler erinnern, dann erinnern Sie sich auch an die Gefahren, wenn man nur die Beispiele zählt, die zur eigenen Position passen. Deshalb werden Sie auch
nachfragen, in wie vielen Fällen die Mutter die Geburt nicht überlebt hat und wie die Zahlen z. B. für den zweiten Flügel der Wiener Klinik aussehen:
Wenn Sie jetzt alle vier Zahlen vergleichen, dann wird überdeutlich, dass 4010 mal „bei uns hat
es geholfen“, kein Zeichen für eine wirksame Behandlung, sondern für ein katastrophales Problem ist. Und probieren Sie es mal aus – wenn man nur eine der vier Zahlen aus obiger Statistik entfernt, dann können Sie keine klaren Aussagen mehr treffen – also immer aufgepasst, wenn man Ihnen Zahlen ohne Vergleichswerte präsentiert!

Dem Mediziner Semmelweis kam bei der Lösung des Problems, warum sterben soviel mehr Frauen in
der einen Abteilung als in der anderen, ein tragischer Zufall zu Hilfe. Ein Freund von ihm starb, nachdem er sich bei einer Autopsie einer Leiche mit dem Skalpell durch den Handschuh und in die Hand schnitt. Die daraus folgende Infektion entwickelte ähnliche Symptome wie Frauen mit Kindbettfieber. Damit erklärte sich auch der Unterschied zwischen den beiden Kliniken – in der einen arbeiteten Hebammen und in der anderen Medizinstudenten, die regelmäßig mit Leichen arbeiteten. Semmelweis führte darauf hin im Jahr 1847 die Maßnahme ein, dass vor den Behandlungen der Wöchnerinnen die Mediziner sich die Hände desinfizieren mussten und – belegte dann auch den Erfolg der neuen Maßnahme durch Statistik:
Damit gilt Semmelweis nicht nur und völlig zu recht als „Retter der Mütter“ sondern auch als der erste, der die Statistik in die Medizin einführte; und tatsächlich ist das vielleicht sogar noch der größere Verdienst.
Gedankt wurde es ihm nicht von allen – besonders nicht von Kollegen von ihm – der Gedanke, dass ein Arzt unsauber sein könnte, musste sich erst noch durchsetzen. Dabei sollte man aber auch daran denken, wie schwer es wohl einem selber als Arzt gefallen wäre, sich einzugestehen, dass man – wenn auch aus Unwissenheit und
unbeabsichtigt – den Tod vieler Frauen im Kindsbett verursacht hat.
Diese Überlegungen fallen aber dann unter das Phänomen Kognitive Dissonanz und das ist dann ein Thema für einen anderen Beitrag.
Was kann ich Ihnen noch zum Abschied mitgeben?
Lassen Sie sich nicht vom Einzelfall täuschen – gerade eigene Erfahrung wirken immer sehr überzeugend, aber zu groß sind hier Fehlerquellen wie Bestätigungsfehler.
Statistiken wirken kalt und unpersönlich – aber hier sind viele Fehlerquellen ausgeschalten.
Rauchen ist nun mal ungesund – egal wie viele Raucher sich auch auf Helmut Schmidt berufen!





Ein sehr schöner Beitrag mit Bildern, der viele der Fehlschlüsse, die unserem Gehirn unterlaufen, anschaulich darstellt.
Ein sehr nett geschrieber Text zu dem Thema.
Wer jetzt noch gerne mehr darüber wissen möchte,
dem empfehle ich das Buch “Fallstricke –
Die häufigsten Denkfehler in Alltag und Wissenschaft”
von Ulrich Frey. Das ist eine wissenschaftlich
fundierte Aufarbeitung des Themas und sehr informativ
Dazu kann ich nur das wunderbare Buch „Thinking: Slow and Fast“ von Daniel Kahnemann empfehlen. Wie unzuverlässig in vielen Situationen „Intuition“ ist und wie wir uns eigentlich ständig durch den Tag irren, ist dort anhand wundervoller (psychologischer) Experimente dargestellt. Aus einer Rezension in der Süddeutschen dazu:
„Ein Experiment Kahnemans und Tverskys ergab etwa, dass bei der Schätzung des Prozentsatzes afrikanischer Staaten in der UN die Höhe Antwort massiv davon beeinflusst werden, welche Zahl ein Probant [sic] kurz vorher an einem Glücksrad gedreht hat. Je höher die Zahl am Glücksrad, desto höher danach der geschätzte Prozentsatz afrikanischer Staaten in der UN. Weniger harmlos klingt es, wenn Kahneman berichtet, dass in einem Experiment erfahrene deutsche Richter eine Ladendiebin zu einer höheren Haftstrafe verurteilten, wenn sie zuvor eine hohe Zahl gewürfelt hatten.“
SZ, vom 25.12.2014
Den Bestätigungsfehler kenne ich eigentlich als selektive Wahrnehmung. Gemeint ist wohl dasselbe, aber nichts desto trotz toller Beitrag. Eigentlich gehört das Thema auf die Lehrpläne, und möglicherweise ist es dort auch zu finden. Aber solange Eso-Tanten den Löwenanteil am Lehrkörper ausmachen, wird das wohl nicht passieren.
Der zweite Teil meines Kommentars war polemisch und das ist auch gut so. Musste mal sein. 😉
Das ist leider falsch: https://scienceblogs.de/kritisch-gedacht/2011/12/08/wunschelruten-an-der-hochschule/
Das stimmt auch nicht. Nicht nur die Medizinalstatistik ist älter, es gab auch vorher schon gut durchdachte Studiendesigns, z.B. die berühmten Nürnberger Kochsalzversuche.
Insofern ist die Frage „Kann ich meinem Hirn trauen?“ wohl zurecht gestellt 😉
Schöner Artikel!
Wer musste beim ersten Bild auch eine Minute lang hingucken um zu checken was da läuft?
Ganz schön hirnwindungsverdehend … 🙂
Falls Du ein wenig trainieren möchtest, PDP10:Adoptiere Mighty Optical Illusions für blogroll oder feed, da kommt mit gewisser Regelmäßigkeit etwas schönes Verwirrendes.
@MX
Danke für die Korrektur – ist natürlich richtig, die Nürnberger Kochsalzversuche waren 1835 ( https://www.nordbayern.de/nuernberger-zeitung/1835-schrieb-nurnberg-medizingeschichte-teil-4-1.216552 ).
Ich hatte diese Versuche immer nur als die ersten Doppelblindversuche im Kopf.
Entschuldigung, dem Experiment von P.C., bzw. der DARAUS abgeleiteten Erkenntnis kann ich nicht zustimmen! Die Zahlenreihe „1, 3, 5“ erfüllt nunmal objektiv die Voraussetzung „+2“, da spielt es doch keine Rolle, ob der Verfasser eigentlich „nur“ das Kriterium „aufsteigende Zahlenfolge“ gemeint oder nicht. Löst jemand die Aufgabe mit „+2“, kann man demjenigen kaum attestieren, etwas zu sehen, was nicht da ist!?
Ich zweifle natürlich nicht daran, dass Menschen Zusammenhänge auch dort sehen wollen, wo keine sind, bloß ist dieses „Experiment“ zum Beweis dieser Tatsache absolut ungeeignet.
@Thorsten #9
Die Aussage „die richtige Reihe“ ist sowieso etwas irreführend. Denn man kann zeigen, dass man mit einer Anzahl n von vorgegebenen Zahlen eine unendliche Anzahl an Formeln angeben kann, die genau diese Reihe erzeugen. D.h. es gibt nicht ‚die eine richtige Lösung‘.
Der Wert des Experiments besteht meiner Meinung nach darin, dass wir als Menschen zwar immer nach Mustern suchen, das wir dabei allerdings eine gewisse, wie soll man das nennen, ‚untere Schwelle der Komplexität‘ überschritten sehen wollen. D.h. es gibt Muster, die zwar für jeden offensichtlich sind, die aber so trivial sind, dass wir sie als einfachste Lösung erst mal nicht in Betracht ziehen.
@Thorsten
@Kallewirsch
Ich habe hier die Beschreibung des Experiments verkürzt wiedergegeben – anscheinend ist da doch einiges verlorengegangen.
Die Aufgabe der Versuchspersonen bestand schon darin, die Regel herauszufinden, nach der die Zahlentripel gebildet wurden. Dazu konnten aber die Versuchspersonen selber Zahlentripel vorschlagen; der Versuchsleiter antwortete dann, ob das Zahlentripel der Regel entsprach.
Insofern entspricht es schon typischen Problemen in den Naturwissenschaften, bei denen man Experimente mit selbstbestimmten Parametern macht, um auf ein zugrundeliegendes Gesetz zu kommen.
Vielleicht hilft ein konkreteres Beispiel. Nehmen wir an, wir hätten die Hypothese „Geburten gibt es nur bei Vollmond“ (also eine zu enge Regel, ähnlich der Regel +2). Dann reicht es nicht, nur an Tagen mit Vollmond ins Krankenhaus zu gehen, um zu sehen, ob es da Geburten gibt – man muss auch an den anderen Tagen prüfen, ob es dann keine Geburten gibt.
Und das war in meinen Augen das wesentliche Ergebnis von P. C. Wason: Nur wenige Versuchspersonen haben Zahlentripel gewählt, die ihrer vermuteten Regel widersprochen haben. Dabei hätte der Versuch, die vermutete Regel zu widerlegen, dazu geführt, dass man eine zu enge Regel aufgeben müsste.
Gegenfrage: kann ich einer Statistik trauen?
Es würden sich ganz leicht ganz viele Beispiele finden lassen, die zeigen dass Statistiken mindestens genauso trügerisch sind als die eigenen Sinne.
Ich würde sogar sagen, die Statistiken sind um einiges unzuverlässiger.
Schöner, gut zu lesender Text, aber ich muss unnötig i-Tipfel-Reiten, noch dazu bei der simplen Einleitung, die ja nur dazu dienen soll, in den Text hineinzukommen und es daher eigentlich völlig unangebracht ist, darüber zu sudern … 😉
Aber diese Annahme ist schon mal nicht richtig: „Oft schmerzlich, wenn die eigene Lieblingstheorie den Bach runter geht, aber mit dem Experiment als unbestechlichen Richter hat die Naturwissenschaft die einzigartige Möglichkeit, Theorien objektiv zu prüfen und falsche Theorien zu erkennen und zu entsorgen. “
Weder wird eine Theorie durch Experiment „objektiv“ geprüft. Denn „objektiv“ bedeutet einen Wahrheitsanspruch. Falsifikation dient höchstens der „objektivierung“, aber nicht um etwas objektiv zu prüfen. Das sind zwei untershciedliche Dinge. Das unterscheidet moderne Wissenschaft vom Positivismus. Noch wird eine Theorie als falsch bewertet, wenn durch ein Experiment ein Widerspruch entsteht.
Diese von Popper abgelehnte Sofortfalsifikation (aber von Kuhn & Co verbreitete Ansicht, das würde Falsifikation bedeuten) stimmt ja ganz offensichtlich nicht, wenn man sich die Wissenschaftsgeschichte ansieht. Denn ansonsten würden wir nun annehmen, es gäbe überlichtschnelle Neutrinos.
Eine Theorie hat – wenn sie wissenschaftlich sein will – falsifizierbare Aussagen zu tätigen. Diese werden dann mit – Kurzvariante: Beobachtungen verglichen. Langvariante: Die Beobachtungen beruhen selbst auf Theorien, wie ich was, wie, wann und warum beobachte. Offensichtlich wird das bei kilometerlangen Ausdrucken von Daten von Radioteleskopen, die erst „richtig“ (also nach einer dahinterstehenden Theorie) interpretiert werden müssen. Diese Theorie, wie ich was beobachte, muss ebenso falsifizierbare Aussagen liefern.
Es werden also im Prozess der Falsifikation falsifizierbare Aussage einer Theorie und einer Theorie der Beobachtung miteinander verglichen. Wenn es zu einem Widerspruch kommt, ist weder die eine noch andere Aussage erstmal falsifiziert und schon gar nicht die dazugehörige Theorien – Theorien sind nicht falsifizierbar, immer nur deren Aussagen.
Entsteht ein Widerspruch, so muss dieser aufgelöst werden. Wenn eine Aussage einer neuen Theorie altbekannte, gut geprüfte Vorstellungen widerspricht, so wirds diese neue Theorie schwer haben. Erlaubt sind dann noch ad-hoc-Hypothesen, die die Theorie durch modifizierte Aussagen nochmals rettet – die Aussagen aus der Theorie plus ad-hoc-Hypothese müssen aber noch falsifizierbarer sein, als die alte Ausage allein.
Das ist die von Popper angestrebte Systemfalsifikation. Ein Widerspruch, eine Falsifikation des Systems, verwirft weder die eine Theorie, noch die andere, sondern zwingt zum nochmaligen Nachdenken, wie das Popper so schön gesagt hat.
Der Kuhn hat das übrigens etwa 10 Jahre später eingesehen und sein großes Werk, das imemr wieder gerne verwendet wird, um Popper zu widerlegen, widerrufen. Bissl peinlich ists für Kuhn geworden, nach dem gezeigt wurde, dass einige Thesen, die er gegen den kritischen Rationalismus vorgebracht hat, er offensichtlich in einer Vorlesung 1950 bei Popper mitbekommen hat. 😉
@Realistischer
Das hängt ganz davon ab, wie ausführlich die fragliche Statistik dokumentiert ist. Dem lakonischen Bildchen in der Tageszeitung braucht man gemeinhin nicht zu trauen, weil da steht ja nix zu den Hintergründen der Statistik drin. Aber einer echten Statistik darf man schon trauen. Denn in der kann man (Statistikkenntnisse vorausgesetzt!) sich sehr gut selber ein Bild machen, worauf sich die in der Statistik abgeleiteten Aussagen abstützen. Da kann man dann auch die Punkte finden, warum man der konkret vorliegenden Statistik vielleicht tatsächlich in einem der Punkte besser nicht so stark trauen sollte.
Das trifft auf diese Bildchen in den Tageszeitungen sicherlich zu. Das gemeine ist, daß die immer behaupten eine Statistik zu sein wobei sie genau genommen gar keine Statistiken sind, sondern bestenfalls das bewertete Schlussergebnis einer vollständigen Statistik. Da fehlt jegliche Hintergrundinformation und lässt somit eine objektive Bewertung nicht mehr zu. Das ist, wie wenn man ein wissenschaftliches Paper mit 50 Seiten Text nur anhand seines Abstracts mit 5 Sätzen bewerten soll.
Das ist einfach zuwenig Info, das geht nicht. Leider wollen Tageszeitungen den eigentlich notwendigen Platz nicht spendieren. Das kann ich aber verstehen, weil die meisten lieben Mitmenschen die vollständige Statistik genausowenig lesen wollen wie das wissenschaftliche Paper mit seinen 50 Seiten.
-_-
@Realistischer
„Gegenfrage: kann ich einer Statistik trauen?“
Mit ist jetzt so auf der Schnelle kein Beispiel eingefallen, wo die Statistik trügerischer wäre als die eigenen Sinne. Vorteil von Statistiken ist in meinen Augen, dass einige Fehler unseres Gehirns (Auswahlfehler, selektive Wahrnehmung, Wunschdenken) ausgeschalten werden.
Aber wie Basilius richtig anführt, darf man Statistiken auch nicht überinterpretieren und mehr in sie hineinlesen, als was drinnen steht. Vielleicht einer der häufigsten Fehler ist dann, von einer Korrelation auf eine Kausalität zu schließen. Meine Lieblingswebseite zu diesem Thema ist Spurious Correlations: https://www.tylervigen.com/
Mehr auch unter: https://www.wissenbloggt.de/?p=24140
@Balisius, Peter Hank
Es ist also so, dass man Statistiken qualifiziert hinterfragen muss, um nicht jedem Täuschungsversuch aufzusitzen. Wenn ich die eigenen Gedanken und Wahrnehmungen ebenso qualifiziert hinterfrage, dann sitze ich ebenso keiner Täuschung auf. D.h., es liegt nicht an Statistik vs. Hirn sondern am (un)qualifizierten Umgang damit.
@Realistischer
Richtig!
Und gut zusammengefasst.
Mit einer Statistik kann ich genauso wie mit jedem anderen Dokument (z.B. wissenschaftliches Paper, Zeitungsartikel, Blogartikel, etc…) einen Sachverhalt beschreiben. Und genauso kann ich hier absichtlich schummeln, meine subjektive Meinung/Erwartung/etc… einfließen lassen oder nach besten Wissen und Gewissen etwas schreiben, was vielleicht dennoch falsch ist weil ich es selber einfach nicht erkannt habe.
Und dann gibt es noch die Fälle, in denen das Geschriebene einfach stimmt.
^_^