Die perfekte Theorie (2): Die Lichter am Himmel sind alle schief!

Dieser Artikel ist Teil einer fortlaufenden Besprechung des Buchs „Die perfekte Theorie: Das Jahrhundert der Genies und der Kampf um die Relativitätstheorie“* (im Original „The Perfect Theory: A Century of Geniuses and the Battle over General Relativity“* von Pedro Ferreira. Jeder Artikel dieser Serie beschäftigt sich mit einem anderen Kapitel des Buchs. Eine Übersicht über alle bisher erschienenen Artikel findet man hier
——————————————————-

Im ersten Kapitel des Buchs haben wir erfahren, was eigentlich das allgemeine an der Allgemeinen Relativitätstheorie ist und wie Albert Einstein überhaupt auf die Idee kam, sie zu entwickeln. Kapitel 2 beschäftigt sich nun mit der langwierigen Suche nach der korrekten Formulierung dieser Theorie und ihrer praktischen Überprüfung.

Einstein war kein großer Freund der Mathematik und dachte sich lieber Gedankenexperimente aus. Er wusste ja schon von seinen bisherigen Überlegungen, dass es einen Zusammenhang zwischen Beschleunigung und Gravitation geben musste. Nun stellte er sich vor, wie sich das Licht verhält, wenn man es von einem beschleunigten Raumschiff aus beobachtet. Wenn das Raumschiff still steht, ist es ganz einfach: Das Licht fällt durch das Fenster auf der einen Seite ein und durch das Fenster genau gegenüber wieder hinaus. Wenn sich das Raumschiff gleichförmig bewegt, dann fällt das Licht durch das eine Fenster ein und ein Stück weiter hinten durch ein anderes Fenster wieder hinaus (wir gehen mal davon aus, dass es eine entsprechendes Fenster an der richtigen Stelle gibt). Der Lichtstrahl ist aber immer noch eine gerade Linie, die eben jetzt nur ein wenig schief durchs Raumschiff verläuft. Wenn es aber beschleunigt, also seine Geschwindigkeit ständig verändert, dann ist der Lichtstrahl vom Raumschiff aus nicht mehr gerade, sondern gebogen! Und da Einstein ja schon festgestellt hatte, dass sich Gravitation und Beschleunigung nicht voneinander unterscheiden lassen, muss man genau den gleichen Effekt auch beobachten, wenn sich das Raumschiff ihn Ruhe aber im Gravitationsfeld eines Planeten befindet.

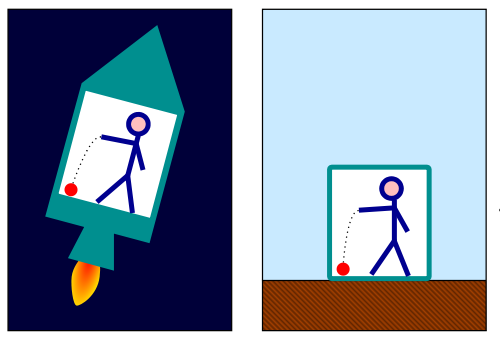
Gravitation lenkt das Licht ab! Aber um die Ergebnisse dieses Gedankenexperiments vernünftig zu formuliere, kam Einstein dann um die Mathematik nicht mehr herum. Er musste sich mit der Geometrie gewölbter bzw. beliebiger Oberflächen beschäftigen, also mit der Differentialgeometrie die der Mathematiker Bernhard Riemann vor damals nicht allzu langer Zeit entwickelt hatte. Einstein hatte Schwierigkeiten mit diesen mathematischen Methoden und arbeitet mit seinem Freund, dem Mathematiker Marcel Grossmann zusammen, mit dem er 1913 auch den Artikel „Entwurf einer verallgemeinerten Relativitätstheorie und einer Theorie der Gravitation“ veröffentlichte. Die Allgemeine Relativitätstheorie machte Fortschritte, aber so ganz funktionierte sie immer noch nicht. Aber Einstein lernte die Mathematik immer besser zu verstehen und im November 1915 schaffte er es dann schließlich, ein paar elegante Gleichungen zu veröffentlichen, die genau das taten, was sie tun sollten.

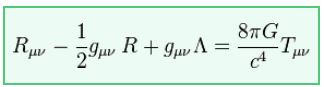
Die Einsteinschen Feldgleichungen stellen ein Gravitationsgesetz dar, das in jedem Bezugssystem gilt. Sie beschreiben, wie Lichtstrahlen in der Nähe von Massen abgelenkt werden und sie sagten die Bewegung des Planeten Merkur mit großer Genauigkeit voraus. Das war etwas, was Newtons Gleichungen nicht gekonnt hatten und nun war auch klar, warum: Das Newtonsche Gravitationsgesetz war nur eine Näherung, die sich aus Einsteins Feldgleichungen ergibt, wenn man allzu große Gravitationskräfte ignoriert. Bei Merkur, der sich in unmittelbarer Nähe zur Sonne befindet ist das aber nicht mehr möglich und deswegen braucht man Einsteins exaktes Gesetz und nicht Newtons Näherung, um seine Bahn zu berechnen.

Aber elegante Gleichungen alleine reichten nicht aus. Auch nicht die Erklärung von Merkurs Bahn. Einsteins Theorie musste eine echte Vorhersage machen, die sich konkret messen und überprüfen lässt. Und die existierte: Lichtstrahlen, die in der Nähe der Sonne vorbei kamen, sollten laut Einsteins Theorie abgelenkt werden. So stark, dass sich der Effekt messen lässt. Man müsste sich nur ein paar Sterne ansehen, wenn sie in unmittelbarer Nähe der Sonne stehen und diese Positionen mit den Positionen vergleichen die die Sterne haben, wenn die Sonne sich weiter bewegt hat und ganz woanders steht. Wenn die Sonne Lichtstrahlen wirklich ablenkt, sollte sich die scheinbare Position der Sterne verändert haben.

Nur leider ist es nicht so einfach, Sterne in unmittelbarer Nähe der Sonne zu beobachten. Das geht nur bei einer totalen Sonnenfinsternis und die gibt es nicht so oft. Aber zum Glück war da der britische Astronom Arthur Eddington. Vor dem ersten Weltkrieg war er einer der wenigen Wissenschaftler, die sich mit Einsteins Arbeiten beschäftigt hatten und sie auch verstanden. Während des Kriegs litt das Ansehen der Deutschen in England aber massiv und auch die Arbeiten deutscher Wissenschaftler gerieten in Verruf. Eddington war, so wie Einstein, ein überzeugter Pazifist und interessierte sich nicht sehr für den aufkommenden Nationalismus. Er beschäftigte sich weiter mit Einsteins Theorien und war von den Feldgleichungen begeistert. Und es gelang ihm, die Behörden davon zu überzeugen, dass es sich lohnt eine Expedition auszurüsten, um die Sonnenfinsternis am 29. Mai 1919 zu beobachten. Hier konnte man prüfen, ob Einsteins Theorie stimmt oder nicht.

Eddington machte sich auf zur Insel Príncipe vor der afrikanischen Küste, hatte ständig schlechtes Wetter und konnte am Tag der Finsternis nur zwei Aufnahmen mit ausreichend guter Qualität machen. Aber die zeigten genau den Effekt, den Einstein vorhergesagt hat. Der Präsident der Royal Society, J.J. Thompsons, nannte die Theorie „eine der größten Leistungen menschlichen Denkens“ und die New York Times titelte aufgeregt aber physikalisch zweifelhaft: „Alle Lichter am Himmel sind schief!“ („All Lights Askew in the Heavens“).

(Wer Lust hat, kann sich die Geschichte von Einstein und Eddington auch in dem netten Spielfilm „Einstein & Eddington“* der BBC ansehen. Es ist vielleicht keine exakte historische Rekonstruktion der Geschehnisse, aber ein unterhaltsamer Film. Und David Tennant spielt Eddington – was will man mehr?)

Die Genauigkeit von Eddingtons Daten war nicht sehr hoch, aber in den nächsten Jahren wurde das Experiment immer wieder wiederholt und das Ergebnis bestätigt. Albert Einstein hatte Recht. Und keine Ahnung, was seine Theorie in den nächsten Jahren für einen Aufruhr in der Wissenschaft erzeugen sollte…

*Affiliate-Links