Mathe-Metal mit dem goldenen Schnitt

Die Zahl Φ ist völlig irrational! Damit ist nicht gemeint, dass man mit ihr kein vernünftiges Gespräch führen kann. Eine irrationale Zahl ist eine Zahl, die nicht als Verhältnis zweier ganzer Zahlen ausgedrückt werden kann. Die Zahl 1,5 zum Beispiel kann man als 3/2 schreiben. Die Zahl 4,985 lässt sich als 997/200 ausdrücken und die Zahl 5 als 5/1. Alle Zahlen, die sich auf diese Weise als Bruch schreiben lassen, nennt man rationale Zahlen. Es gibt aber auch welche, bei denen das nicht funktioniert. Die Wurzel aus 2 zum Beispiel. Egal wie sehr man sich anstrengt, man wird keine zwei ganzen Zahlen finden, deren Verhältnis exakt dem Wert der Wurzel aus 2 entspricht. Das sind die irrationalen Zahlen. Und Φ, die Zahl des goldenen Schnitts, ist von allen am irrationalsten!

Manche irrationalen Zahlen lassen sich sehr gut durch rationale Zahlen annähern. Pi zum Beispiel. Die Kreiszahl Pi selbst (3,14159265…) kann nicht durch einen Bruch dargestellt werden. Der Bruch 22/7 ist aber eine ganz gut Näherung (darum feiern die Freunde der Zahl Pi auch jedes Jahr am 22. 7 – also morgen – den „Pi-Approximationstag“). Wie gut eine irrationale Zahl approximierbar ist, erkennt man an ihrer Kettenbruchdarstellung

Ein Kettenbruch sieht so:

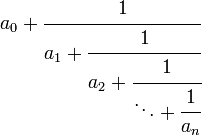
Keine Angst, das ist nicht so schlimm, wie es aussieht 😉 Ich erkläre es mal (und wer absolut keine Lust auf Mathe hat, kann gerne auch gleich zum coolen Video am Ende scrollen).

Tun wir mal so, als seien wir Christiaan Huygens, der berühmte Astronom aus dem 17. Jahrhundert. Wir wollen ein Modell des Sonnensystems bauen und friemeln an den verschiedenen Zahnrädern herum. Damit die Planeten sich im Verhältnis alle zueinander richtig bewegen, müssen die Zahnräder die richtige Anzahl an Zähnen haben. Und um die richtige Anzahl an Zähnen zu bestimmen, müssen wir das Verhältnis der Umlaufzeiten der Planeten irgendwie durch eine rationale Zahl approximieren, und zwar möglichst gut. Der Saturn zum Beispiel braucht für einen Umlauf um die Sonne 10759,16925 Tage. Bei der Erde sind es bekanntlich 365,25 Tage. Das Verhältnis beträgt also 29,457 (was nichts anderes bedeutet, als das Saturn 29,457 Jahre für einen Umlauf um die Sonne braucht). Das sind die heute bekannten Werte; damals fand Huygens heraus, dass sich
das Verhältnis der Umlaufzeiten durch den Bruch 77708431/2640858 gut darstellen lässt. Allerdings ist das eine ziemlich unhandliche Zahl und der Bruch lässt sich auch nicht mehr weiter vereinfachen. Aber Huygens war klug und benutzte die Kettenbrüche!

Zuerst rechnen wir den Bruch einfach mal aus. 77708431 dividiert durch 2640858 ergibt 29,425448… (Es ist wirklich eine sehr unangenehme Zahl. Die Nachkommstellen sind zwar periodisch, es ist ja eine rationale Zahl, aber das sieht man erst nach 20006 Stellen). Die erste, noch sehr ungenaue Approximation wäre also 29/1. Wir wollen es aber genauer haben. Der Fehler unserer Annäherung beträgt jetzt 0,425448… Das ist ungefähr 0,5 – also 1/2. Genauer gesagt ist es 1/2,3504609… Damit haben wir nun eine bessere Approximation gefunden: 29 + 1/2. Aber wir machen immer noch einen Fehler. Nun haben wir 2,3504609… durch 2 approximiert. Also widmen wir uns dem Teil, den wir gerade vernachlässigt haben: 0,3504609… können wir auch als 1/2,853385… schreiben. Eine bessere Approximation für 2,3504609… als 2 wäre also die Zahl 2 + 1/2. Bevor jetzt alles unübersichtlich wird, setzen wir mal alles zusammen.

Wir haben bei unserer Approximation 29 angefangen. Das haben wir mit 29+1/2 verbessert. Die 2 unterm Bruchstrich haben wir durch die Zahl 2+1/2 verbessert. Unsere Approximation lautet nun also

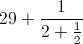
Natürlich können wir weitermachen. Wir haben ja immer noch einen Fehler in unserer Approximation. Die letzte 2 im Bruch sollte eigentlich eine 2,853385… sein; wir aber haben die 0,853385… einfach unter den Tisch fallen lassen. 0,853385… ist fast 1. Wir können anstatt der 2 also auch einfach 2+1 schreiben. Unsere Approximation wird dann insgesamt zu:

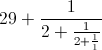
Das Prinzip sollte mittlerweile klar sein, oder? Als nächstes käme dann

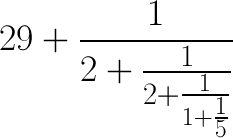
Und so kann man das Spiel immer weiter spielen. Der entstehende Kettenbruch wird die ursprüngliche Zahl immer genauer approximieren. Aber für uns reicht es erstmal. So einen Kettenbruch kann man natürlich auch wieder in einen normalen Bruch umrechnen. Unsere erste Approximation war 29 + 1/2. Umgerechnet ergibt das 59/2. Die nächste Approximation war 29 + 1/(2+1/2), was dem Bruch 147/5 entspricht. Der nächste verbesserte Kettenbruch liefert 206/7 und der letzte Kettenbruch, bei dem wir dann gestoppt haben, vereinfacht sich zu 1177/40. Dank der Methode mit den Kettenbrüchen haben wir also einen einfachen Weg, um eine Reihe von Brüchen zu finden, die unsere Ausgangszahl immer besser approximieren!

Christiaan Huygens hatte damals bei 206/7 halt gemacht. Dieser Bruch näherte das Verhältnis der Umlaufzeiten von Saturn und Erde ausreichend gut an. Das Zahnrad für den Saturn brauchte also 206 Zähne, das für die Erde nur 7 – dann würden sie sich ausreichend genau mit der richtigen Geschwindigkeit bewegen!

Aber was hat das alles mit dem goldenen Schnitt zu tun? Der „goldene Schnitt“ ist das berühmte Teilungsverhältnis, dass man überall in der Kunst und der Natur findet. Man teilt dabei eine Strecke so, dass das Verhältnis der Gesamtstrecke zum größeren Abschnitt dem Verhältnis des größeren zum kleineren Abschnitt entspricht. Nennt man diese beiden Abschnitte a und b, dann kann mit ein wenig Geometrie (ich zeig das jetzt nicht vor) leicht ausrechnen, dass das Verhältnis a/b immer einen bestimmten Wert haben muss. Diese Zahl nennt man Φ, die Zahl des goldenen Schnitts:

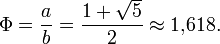
Diese Zahl ist irrational, sie lässt sich also nicht als Bruch mit zwei ganzen Zahlen schreiben. Aber natürlich kann man mit ihr das gleiche Spiel spielen, wie Huygens mit seinem Verhältnis von Planetenumläufen. Tut man das, dann bekommt man einen äußerst interessanten Kettenbruch:

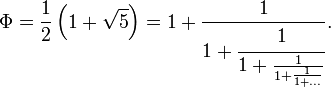
Er besteht nur aus Einsen! Was bedeutet das? Erinnern wir uns an die Art und Weise, wie man den Kettenbruch konstruiert: Man bestimmt einen Näherungsbruch, und berechnet den Fehler. Dieser Fehler wird dann wieder in einen Näherungsbruch umgewandelt, der an den ursprünglichen Bruch dran gehängt wird. Dann berechnet man den Fehler davon, und so weiter. Wichtig ist, dass der Fehler immer unter dem Bruchstrich steht. Ist der Fehler klein, dann muss die Zahl unter dem Bruchstrich groß sein (1/10 ist ein wesentlich kleinerer Fehler als 1/2). Ist der Fehler groß, dann ist die Zahl klein. Wenn also in der Kettenbruchentwicklung von Φ nur Einsen, also nur kleine Zahlen vorkommen, dann heißt das, dass wir bei jedem Schritt der Approximation einen großen Fehler machen. Schlechter geht es in diesem Fall nicht mehr. Die Zahl des goldenen Schnitts ist von allen irrationalen Zahlen diejenige, die sich am schlechtesten durch einen Bruch nähern lässt!

Das ist übrigens auch der Grund, warum sie in der Natur so oft zu finden ist. Da ist es nämlich oft von Vorteil, wenn bestimmte Dinge, wie zum Beispiel die Anordnung von Blättern oder Blütenständen bei Pflanzen, möglichst schlecht approximierbar sind. Ein Blättermuster, dass sich schnell exakt wiederholt, also mit einer Periode die durch einen kleinen Bruch approximierbar ist, führt z.B. dazu, dass die Blätter direkt übereinander stehen und sich gegenseitig das Licht wegnehmen (ich habe das hier genauer erklärt).

Mit dem goldenen Schnitt lässt sich aber auch noch jede Menge anderes cooles Zeug anstellen. Sie eignet sich offensichtlich ideal, um daraus ein Metal-Lied zu machen. Im „Golden Ratio Song“ wird nicht nur über den goldenen Schnitt gesungen, auch die Musik selbst wird durch Φ bestimmt. Das Ergebnis ist genial:

Im „Making of“ des Videos wird nochmal ausführlich erklärt, wo der goldene Schnitt überall auftaucht:

Es gibt übrigens tatsächlich eine Musikrichtung, die Math Metal heißt. Aber diese Art von Mathe-Metal gefällt mir besser 😉